Jak korzystać z rozkładu trójkątnego w r (z przykładami)
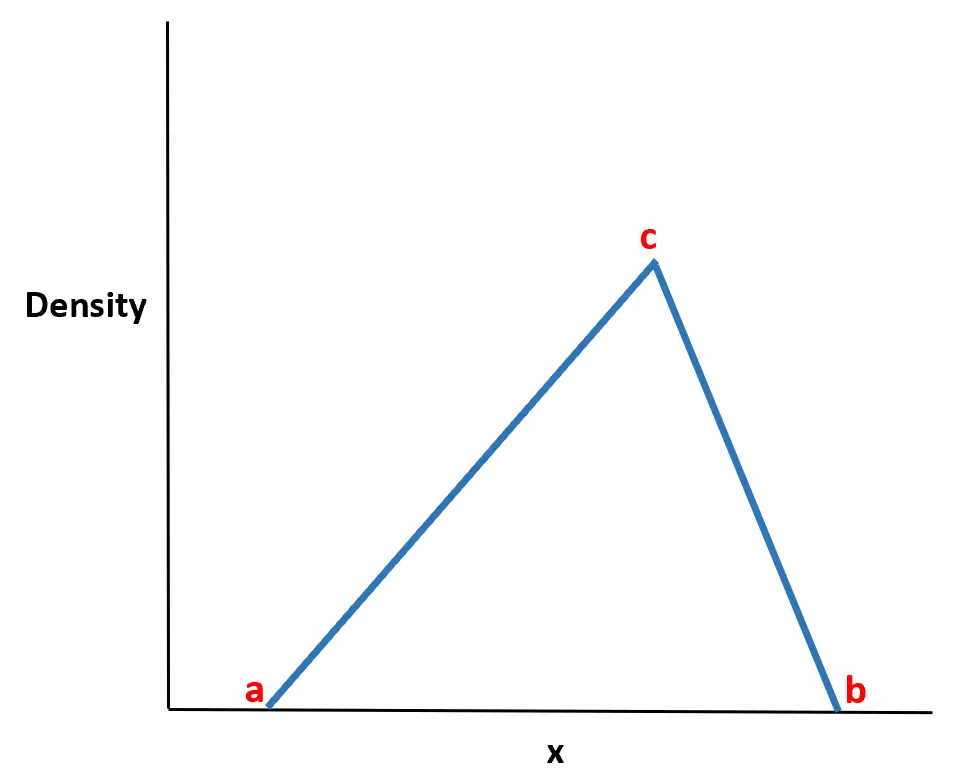
Rozkład trójkątny jest ciągłym rozkładem prawdopodobieństwa z funkcją gęstości prawdopodobieństwa w kształcie trójkąta.
Jest ona definiowana przez trzy wartości:
- Wartość minimalna ma
- Maksymalna wartość B
- Maksymalna wartość c
Aby obliczyć prawdopodobieństwa rozkładu trójkątnego w R, możemy skorzystać z funkcji ptri( ) z pakietu EnvStats , która wykorzystuje następującą składnię:
ptri(q, min = 0, max = 1, tryb = 1/2)
Złoto:
- q : Kwantyl będący przedmiotem zainteresowania
- min : Minimalna wartość rozkładu
- max : Maksymalna wartość rozkładu
- mode : Wartość szczytowa rozkładu
Poniższe przykłady pokazują, jak w praktyce wykorzystać tę funkcję w R.
Przykład 1: Obliczanie prawdopodobieństwa mniejszego od określonej wartości
Załóżmy, że restauracja szacuje, że jej łączna sprzedaż w nadchodzącym tygodniu wyniesie co najmniej 10 000 USD, maksymalnie 30 000 USD i najprawdopodobniej 25 000 USD.

Jakie jest prawdopodobieństwo, że łączna sprzedaż restauracji będzie mniejsza niż 20 000 USD?
Do obliczenia tego prawdopodobieństwa możemy użyć następującego kodu:
library (EnvStats) #calculate probability ptri(q = 20000, min = 10000, max = 30000, mode = 25000) [1] 0.3333333
Prawdopodobieństwo, że łączna sprzedaż restauracji będzie mniejsza niż 20 000 USD, wynosi 0,333 .
Przykład 2: Obliczanie prawdopodobieństwa większego niż określona wartość
Załóżmy, że sklep szacuje, że liczba klientów, którzy przyjdą w danym tygodniu, wyniesie minimum 500, maksymalnie 2000 i najprawdopodobniej 1200.
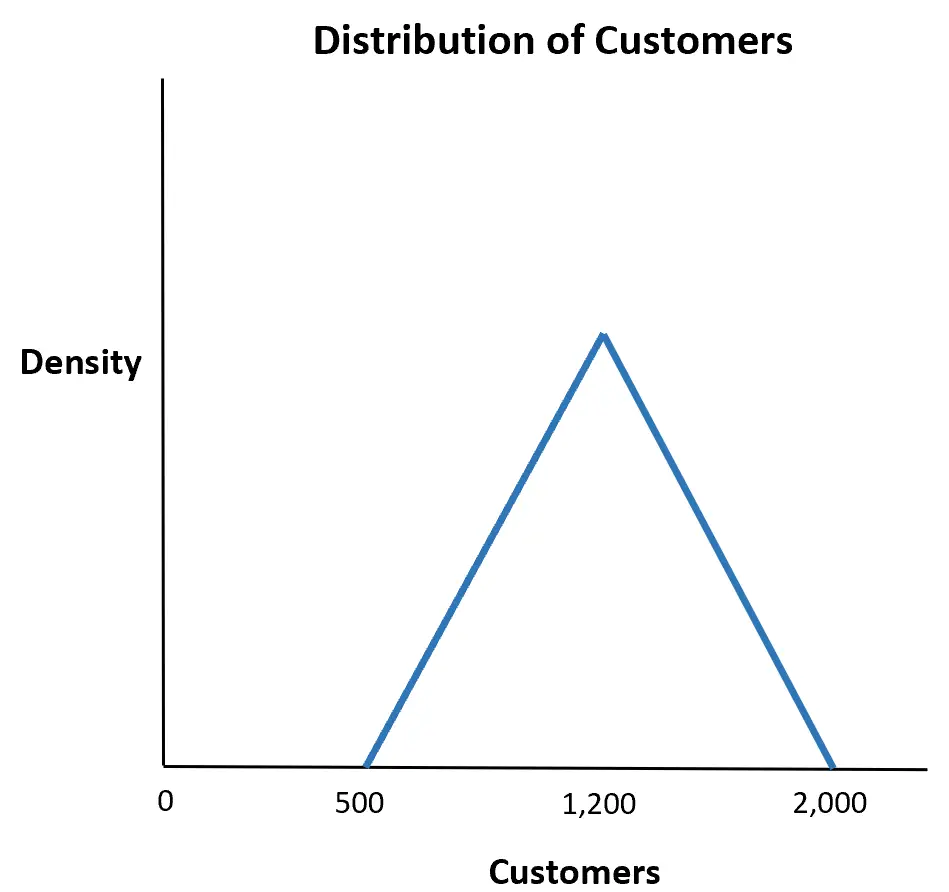
Jakie jest prawdopodobieństwo, że w danym tygodniu do sklepu wejdzie więcej niż 1500 klientów?
Do obliczenia tego prawdopodobieństwa możemy użyć następującego kodu:
library (EnvStats) #calculate probability 1 - ptri(q = 1500, min = 500, max = 2000, mode = 1200) [1] 0.2083333
Prawdopodobieństwo, że do sklepu wejdzie więcej niż 1500 klientów, wynosi około 0,208.
Uwaga : Pełną dokumentację funkcji ptri() można znaleźć tutaj .
Dodatkowe zasoby
Poniższe tutoriale wyjaśniają, jak używać innych rozkładów prawdopodobieństwa w R:
Jak korzystać z rozkładu normalnego w R
Jak korzystać z rozkładu dwumianowego w R
Jak korzystać z rozkładu Poissona w R
Jak korzystać z rozkładu wielomianowego w R