Quasiwariancja

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest kwazowariancja w statystyce. W ten sposób dowiesz się, jak obliczyć kwaziwariancję, rozwiązane zadanie i jakie są różnice między kwaziwariancją a wariancją. Dodatkowo możesz obliczyć kwazowariancję dowolnego zbioru danych za pomocą kalkulatora online.

Co to jest kwazowariancja?

W statystyce kwazowariancja jest miarą rozproszenia wskazującą zmienność próbki. Dokładniej, kwazowariancja jest równa sumie kwadratów odchyleń podzielonej przez całkowitą liczbę obserwacji minus jeden.

Symbolem kwazowariancji jest

$\sigma_{n-1}^2$

albo

$s_{n-1}^2$

. czasami Chociaż symbol jest również używany

$\widehat{s}^2$

do reprezentowania kwazowariancji.

Kwasiwariancję stosuje się do określenia rozproszenia próbki przy jednoczesnym unikaniu błędu systematycznego, dlatego często nazywa się ją wariancją bezstronną. Kwaziwariancja jest zatem dobrym estymatorem wariancji populacji. W rzeczywistości przy obliczaniu wariancji próbki zamiast wzoru na wariancję często stosuje się wzór quasi-wariancyjny. Poniżej szczegółowo omówimy różnicę między tymi dwoma miarami statystycznymi.

Wzór kwazowariancji

Aby obliczyć kwazowariancję, należy znaleźć sumę kwadratów różnic między wartościami i średnią zbioru danych, a następnie podzielić ją przez całkowitą liczbę danych minus jeden.

Zatem wzór na obliczenie kwazowariancji jest następujący:

Złoto:

$\sigma_{n-1}^2$

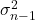
jest kwazowariancją.
$x_i$

jest wartością danych

$i$

.
$n$

to całkowita liczba danych.
$\overline{X}$

jest średnią zbioru danych.

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć kwazowariancję dowolnego zbioru danych.

Być może zastanawiasz się, dlaczego jest on dzielony przez n-1, a nie przez n? Cóż, chodzi o wyeliminowanie obciążenia, w ten sposób otrzymamy nieobciążony estymator. Właśnie dlatego kwaziwariancja jest dobrym estymatorem wariancji populacji.

Przykład obliczenia quasiwariancji

Teraz, gdy znamy definicję kwazowariancji, rozwiążemy prosty przykład, aby zobaczyć, jak obliczana jest kwazowariancja serii danych.

Z międzynarodowej firmy wiemy, jaki wynik gospodarczy osiągnęła w ciągu ostatnich pięciu lat, w większości osiągnęła zyski, ale w jednym roku wykazała znaczne straty: 11,5, 2, -9, 7 mln euro. Oblicz kwazowariancję tego zbioru danych.

Pierwszą rzeczą, którą musimy zrobić, aby uzyskać kwazowariancję zbioru danych, jest obliczenie jego średniej arytmetycznej:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

A kiedy już znamy średnią wartość danych, stosujemy wzór na kwazowariancję:

$\sigma_{n-1}^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

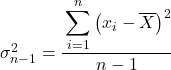
Podstawiamy zatem dane podane w instrukcji ćwiczenia do wzoru:

$\sigma_{n-1}^2=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5-1}$

Na koniec wystarczy rozwiązać operacje, aby obliczyć kwazowariancję:

$\begin{aligned}\sigma_{n-1}^2&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5-1}\\[2ex]&= \cfrac{228,8}{4} \\[2ex]&=57,2 \ \text{millones de euros}^2\end{aligned}$

Należy zauważyć, że jednostki kwazowariancji to te same jednostki, co jednostki danych statystycznych, ale podniesione do kwadratu, więc kwazowariancja tego zbioru danych wynosi 57,2 miliona ² .

➤ Patrz: Odchylenie quasi-standardowe

Kalkulator quasiwariancji

Wprowadź zestaw danych statystycznych do poniższego kalkulatora, aby obliczyć jego kwazowariancję. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

Wariancja i quasiwariancja

Wreszcie zobaczymy różnicę między quasiwariancją a wariancją, ponieważ pomimo podobieństwa w nazwie, są one również obliczane bardzo podobnie.

Różnica między kwaziwariancją a wariancją jest mianownikiem wzoru. Aby obliczyć kwaziwariancję, należy podzielić przez n-1, jednak wariancję oblicza się, dzieląc przez n.

Zatem kwazowariancja i wariancja są matematycznie powiązane, ponieważ kwazowariancja jest równoważna wariancji pomnożonej przez n (całkowita liczba punktów danych) i podzielonej przez n-1.

$\sigma_{n-1}^2=\cfrac{n}{n-1}\cdot \sigma^2$

Dlatego dla tego samego zbioru danych wartość quasiwariancji będzie zawsze większa niż wartość wariancji.

➤ Zobacz: Właściwości odchyłek

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej