Zmienność wewnątrzgrupowa lub międzygrupowa w anova
Jednoczynnikową analizę ANOVA stosuje się do określenia, czy średnie trzech lub większej liczby niezależnych grup są równe.
Jednoczynnikowa ANOVA wykorzystuje następujące hipotezy zerowe i alternatywne:
- H 0 : Wszystkie średnie grupowe są równe.
- H A : Przynajmniej jedna średnia grupowa różni się od pozostałych.
Za każdym razem, gdy przeprowadzasz jednokierunkową analizę ANOVA, otrzymasz tabelę podsumowującą, która wygląda następująco:
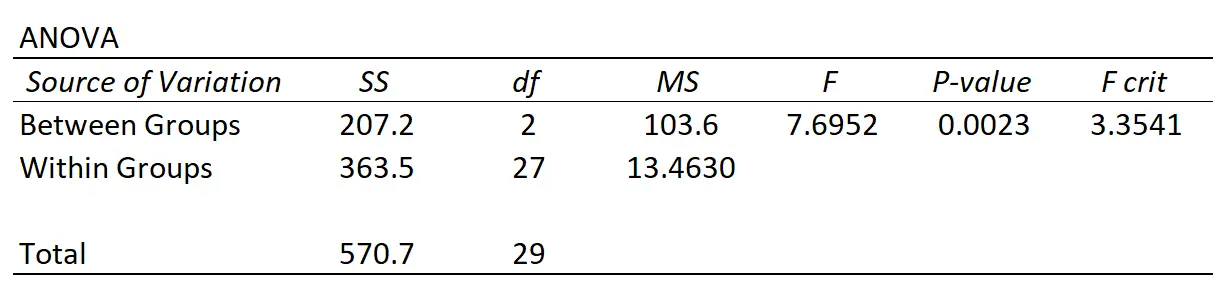
Widzimy, że istnieją dwa różne źródła zmienności mierzone metodą ANOVA:
Różnice między grupami : całkowita różnica między średnią każdej grupy a średnią ogólną.
Zmienność wewnątrzgrupowa : całkowita zmienność poszczególnych wartości w każdej grupie i ich średnia grupowa.
Jeżeli zmienność między grupami jest duża w porównaniu ze zmiennością wewnątrz grupy, wówczas statystyka F analizy ANOVA będzie wyższa, a odpowiadająca jej wartość p będzie niższa, co zwiększa prawdopodobieństwo odrzucenia hipotezy zerowej, zgodnie z którą średnie grupowe są równe.
Poniższy przykład pokazuje, jak w praktyce obliczyć zmienność międzygrupową i wewnątrzgrupową dla jednokierunkowej ANOVA.
Przykład: Obliczanie zmienności w obrębie grupy i pomiędzy grupami w ANOVA
Załóżmy, że chcemy ustalić, czy trzy różne metody nauki prowadzą do różnych średnich wyników egzaminów. Aby to przetestować, rekrutujemy 30 uczniów i losowo przydzielamy 10 każdemu do stosowania innej metody nauki.
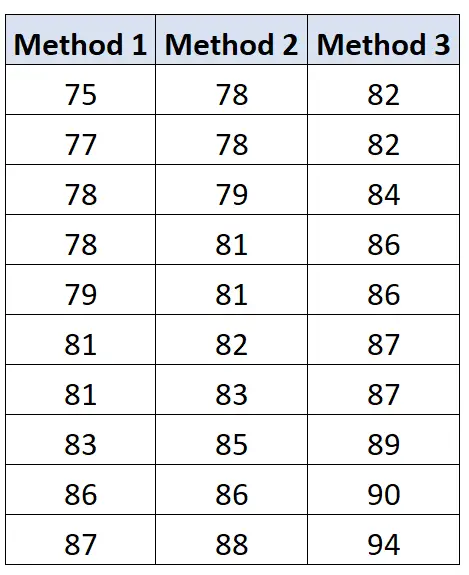
Poniżej wyniki egzaminów uczniów w poszczególnych grupach:
Do obliczenia zróżnicowania pomiędzy grupami możemy użyć następującego wzoru:
Różnica między grupami = Σn j (X j – X ..) 2
Złoto:
- n j : liczebność próby grupy j
- Σ : symbol oznaczający „sumę”
- X j : średnia grupy j
- X .. : średnia ogólna
Aby obliczyć tę wartość, najpierw obliczymy średnią dla każdej grupy i średnią ogólną:
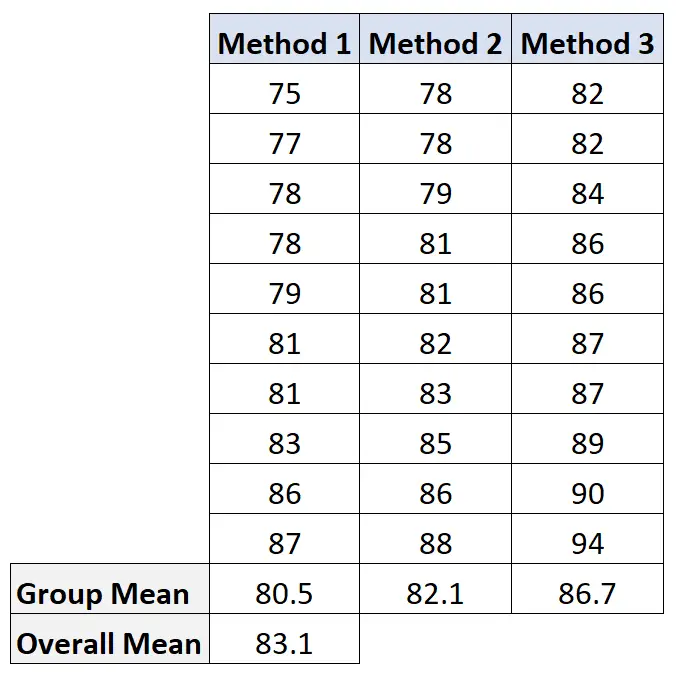
Następnie obliczamy różnicę między grupami w następujący sposób: 10(80,5-83,1) 2 + 10(82,1-83,1) 2 + 10(86,7-83,1) 2 = 207,2 .
Następnie możemy użyć następującego wzoru do obliczenia zmienności wewnątrzgrupowej :
Zmienność wewnątrzgrupowa : Σ(X ij – X j ) 2
Złoto:
- Σ : symbol oznaczający „sumę”
- X ij : i-ta obserwacja grupy j
- X j : średnia grupy j
W naszym przykładzie obliczamy zmienność w obrębie grupy jako:
Grupa 1: (75-80,5) 2 + (77-80,5) 2 + (78-80,5) 2 + (78-80,5) 2 + (79-80,5) 2 + (81-80,5) 2 + (81-80,5) 2 + (83-80,5) 2 + (86-80,5) 2 + (87-80,5) 2 = 136,5
Grupa 2: (78-82,1) 2 + (78-82,1) 2 + (79-82,1) 2 + (81-82,1) 2 + (81-82,1) 2 + (82-82,1) 2 + (83-82,1) 2 + (85-82,1) 2 + (86-82,1) 2 + (88-82,1) 2 = 104,9
Grupa 3: (82-86,7) 2 + (82-86,7) 2 + (84-86,7) 2 + (86-86,7) 2 + (86-86,7) 2 + (87-86,7) 2 + (87-86,7) 2 + (89-86,7) 2 + (90-86,7) 2 + (94-86,7) 2 = 122,1
Zmienność wewnątrz grupy: 136,5 + 104,9 + 122,1 = 363,5
Jeśli użyjemy oprogramowania statystycznego do przeprowadzenia jednokierunkowej analizy ANOVA przy użyciu tego zbioru danych, otrzymamy następującą tabelę ANOVA:
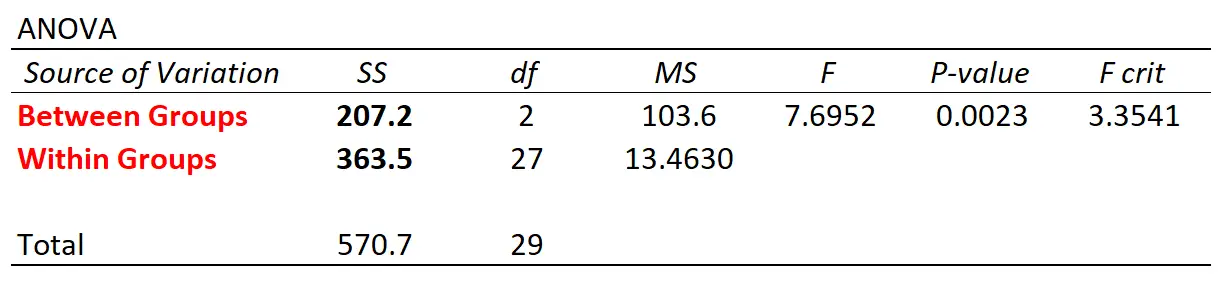
Należy pamiętać, że wartości zróżnicowania międzygrupowego i wewnątrzgrupowego odpowiadają tym, które obliczyliśmy ręcznie.
Ogólna statystyka F w tabeli jest sposobem ilościowego określenia związku między zmiennością między grupami a zmiennością w obrębie grupy.
Im większa statystyka F, tym większa zmienność średnich między grupami w stosunku do zmienności wewnątrz grup.
Zatem im większa statystyka F, tym bardziej oczywiste jest, że istnieje różnica między średnimi grupowymi.
W tym przykładzie widzimy, że wartość p odpowiadająca statystyce F wynoszącej 7,6952 wynosi 0,0023 .
Ponieważ wartość ta jest mniejsza niż α = 0,05, odrzucamy hipotezę zerową analizy ANOVA i dochodzimy do wniosku, że trzy techniki badawcze nie prowadzą do tego samego wyniku na egzaminie.
Dodatkowe zasoby
Poniższe tutoriale dostarczają dodatkowych informacji o modelach ANOVA:
Wprowadzenie do jednokierunkowej ANOVA
Jak interpretować wartość F i wartość P w ANOVA
Kompletny przewodnik: Jak zgłaszać wyniki ANOVA
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej