Jak wykonać test t dla sparowanych próbek w sas

Test t dla par prób służy do porównania średnich z dwóch próbek, gdy każdą obserwację w jednej próbie można powiązać z obserwacją w drugiej próbie.

W tym samouczku wyjaśniono, jak wykonać test t dla sparowanych próbek w SAS-ie.

Przykład: Test t dla par próbek w SAS

Załóżmy, że profesor chce ustalić, czy określony program nauczania wpływa na wyniki testów. Aby to sprawdzić, losowo wybiera 15 uczniów, którzy przystępują do testu wstępnego. Następnie każe każdemu uczniowi korzystać z programu nauczania przez miesiąc, a następnie rozwiązuje test końcowy o podobnym stopniu trudności.

Wyniki testów każdego z 15 uczniów przedstawiono poniżej:

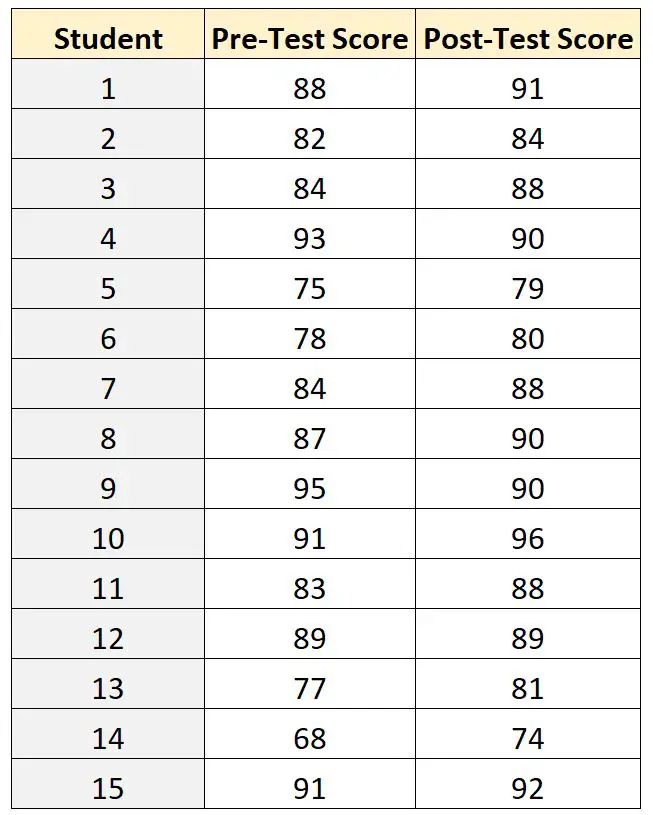
Aby porównać różnicę między średnimi wynikami przed testem i po teście, nauczyciel może zastosować sparowane próbki w teście t, ponieważ w przypadku każdego ucznia jego wynik przed testem można powiązać z wynikiem po teście.

Wykonaj następujące kroki, aby wykonać test t dla sparowanych próbek w SAS:

Krok 1: Utwórz dane

Najpierw użyjmy poniższego kodu, aby utworzyć zbiór danych w SAS-ie:

 /*create dataset*/
datatest_scores ;
    input pre post;
    datalines ;
88 91
82 84
84 88
93 90
75 79
78 80
84 88
87 90
95 90
91 96
83 88
89 89
77 81
68 74
91 92
;
run ;

/*view dataset*/
proc print data =test_scores;

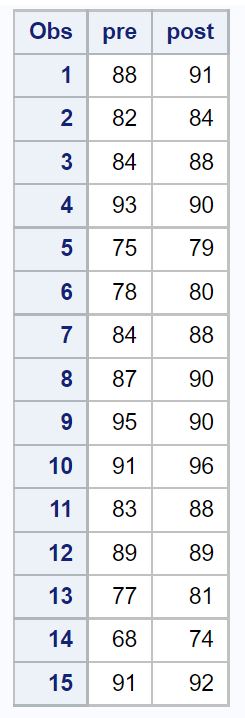
Krok 2: Wykonaj test t dla sparowanych próbek

Następnie możemy użyć proc ttest do wykonania testu t dla sparowanych próbek:

 /*perform paired samples t-test*/
proc ttest data =test_scores alpha = .05 ;
    paired pre*post;
run ; 

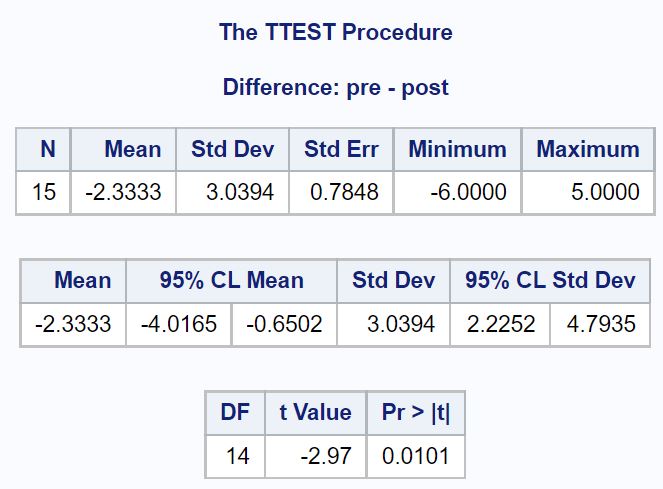
Z wyniku możemy zobaczyć, co następuje:

• Średnia różnica między wynikiem przed i po teście: -2,3333
• 95% przedział ufności dla średniej różnicy: [-4,0165, -0,6502]

Możemy również zobaczyć statystykę testu t i odpowiadającą jej dwustronną wartość p:

• Statystyka testu t: -2,97
• Wartość p: 0,0101

W tym przykładzie test t dla par próbek wykorzystuje następujące hipotezy zerowe i alternatywne:

• H ₀ : Średnie wyniki przed i po teście są równe
• H _A : Średnie wyniki przed i po teście nie są równe

Ponieważ wartość p ( 0,0101 ) jest mniejsza niż 0,05, odrzucamy hipotezę zerową.

Oznacza to, że mamy wystarczające dowody, aby stwierdzić, że prawdziwy średni wynik testu różni się w przypadku uczniów przed i po udziale w programie studiów.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne popularne testy statystyczne w SAS-ie:

Jak wykonać test t dla jednej próby w SAS
Jak wykonać test t dla dwóch próbek w SAS
Jak wykonać test rangowy ze znakiem Wilcoxona w SAS