Rozkład poissona czy rozkład normalny: jaka jest różnica?

Rozkład Poissona i rozkład normalny to dwa najczęściej używane rozkłady prawdopodobieństwa w statystyce.

Ten samouczek zawiera szybkie wyjaśnienie każdej dystrybucji, a także dwie kluczowe różnice między dystrybucjami.

Przegląd: rozkład Poissona

Rozkład Poissona opisuje prawdopodobieństwo uzyskania k sukcesów w zadanym przedziale czasu.

Jeśli zmienna losowa X ma rozkład Poissona, prawdopodobieństwo, że X = k powodzenia można obliczyć za pomocą następującego wzoru:

P(X=k) = λ ^k * e ^{– λ} / k!

Złoto:

• λ: średnia liczba sukcesów występujących w określonym przedziale czasu
• k: liczba sukcesów
• e: stała równa około 2,71828

Załóżmy na przykład, że w konkretnym szpitalu odbywają się średnio 2 porody na godzinę. Z powyższego wzoru możemy określić prawdopodobieństwo wystąpienia 3 porodów w danej godzinie:

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Prawdopodobieństwo przeżycia 3 porodów w ciągu danej godziny wynosi 0,1805 .

Przegląd: rozkład normalny

Rozkład normalny opisuje prawdopodobieństwo, że zmienna losowa przyjmie wartość w danym przedziale.

Funkcję gęstości prawdopodobieństwa rozkładu normalnego można zapisać jako:

P(X=x) = (1/σ√ 2π )e ^{-1/2((x-μ)/σ) 2}

Złoto:

• σ: Odchylenie standardowe rozkładu
• μ: średnia rozkładu
• x: wartość zmiennej losowej

Załóżmy na przykład, że masa określonego gatunku wydry ma rozkład normalny wynoszący μ = 40 funtów i σ = 5 funtów.

Jeśli losowo wybierzemy wydrę z tej populacji, możemy skorzystać z poniższego wzoru, aby znaleźć prawdopodobieństwo, że waży ona od 38 do 42 funtów:

P ( ^{38 < /5) 2} = 0,3108

Prawdopodobieństwo, że losowo wybrana wydra waży od 38 do 42 funtów, wynosi 0,3108 .

Różnica nr 1: Dyskretny vs. Dane ciągłe

Pierwszą różnicą między rozkładem Poissona a rozkładem normalnym jest rodzaj danych modelowanych przez każdy rozkład prawdopodobieństwa.

Rozkład Poissona jest używany podczas pracy z danymi dyskretnymi , które mogą przyjmować tylko wartości całkowite równe lub większe od zera. Oto kilka przykładów:

• Liczba połączeń odebranych na godzinę w call center
• Liczba klientów dziennie w restauracji
• Liczba wypadków samochodowych w miesiącu

W każdym scenariuszu zmienna losowa może przyjmować tylko wartości 0, 1, 2, 3 itd.

Rozkład normalny jest używany podczas pracy z danymi ciągłymi , które mogą przyjmować dowolną wartość od ujemnej nieskończoności do dodatniej nieskończoności. Oto kilka przykładów:

• Waga określonego zwierzęcia
• Wysokość określonej rośliny
• Czasy maratonu kobiet
• Temperatura w stopniach Celsjusza

W tych scenariuszach zmienne losowe mogą przyjmować dowolną wartość, na przykład -11,3, 21,343435, 85 itd.

Różnica nr 2: kształt rozkładów

Druga różnica między rozkładem Poissona a rozkładem normalnym polega na kształcie rozkładów.

Rozkład normalny zawsze będzie miał kształt dzwonu:

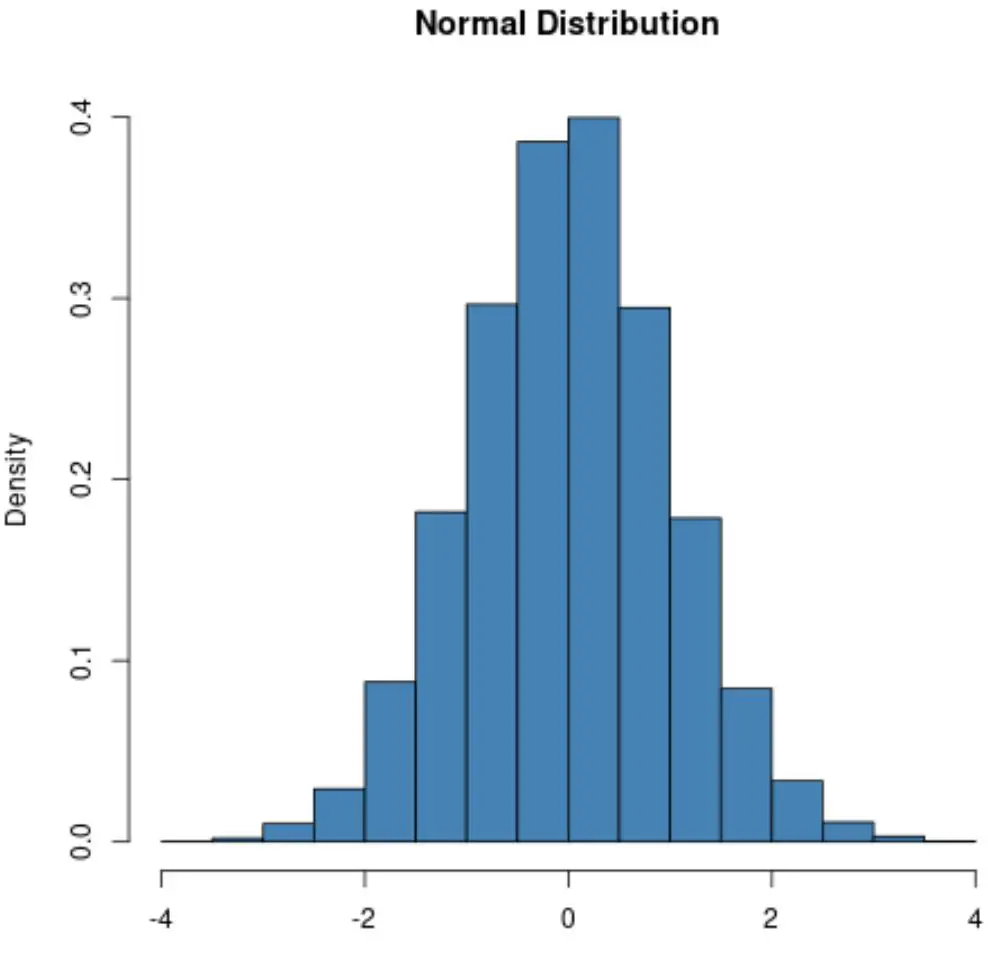
Jednakże kształt rozkładu Poissona zmienia się w zależności od średniej wartości rozkładu.

Na przykład rozkład Poissona z małą wartością średniej, np. μ = 3 , będzie silnie skośny w prawo :

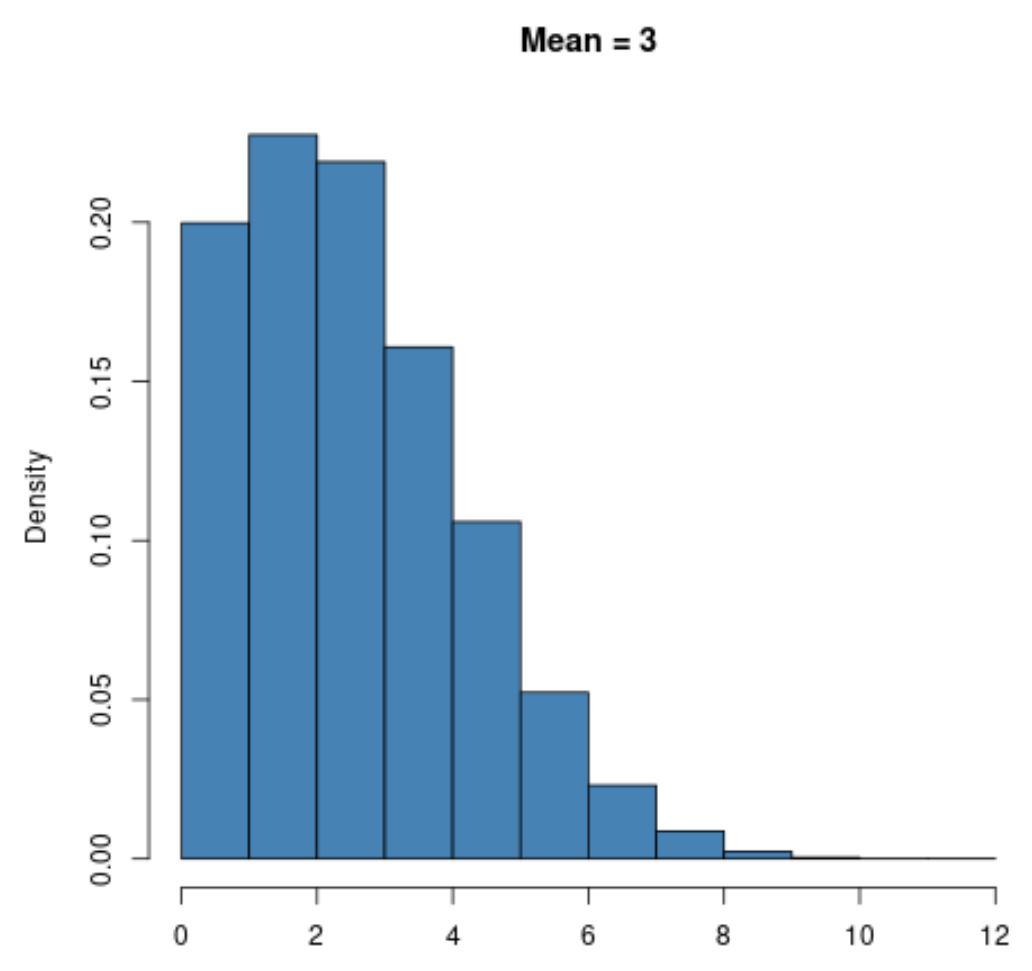
Jednakże rozkład Poissona z większą wartością średnią, np. μ = 20 , będzie miał kształt dzwonu, podobnie jak rozkład normalny:

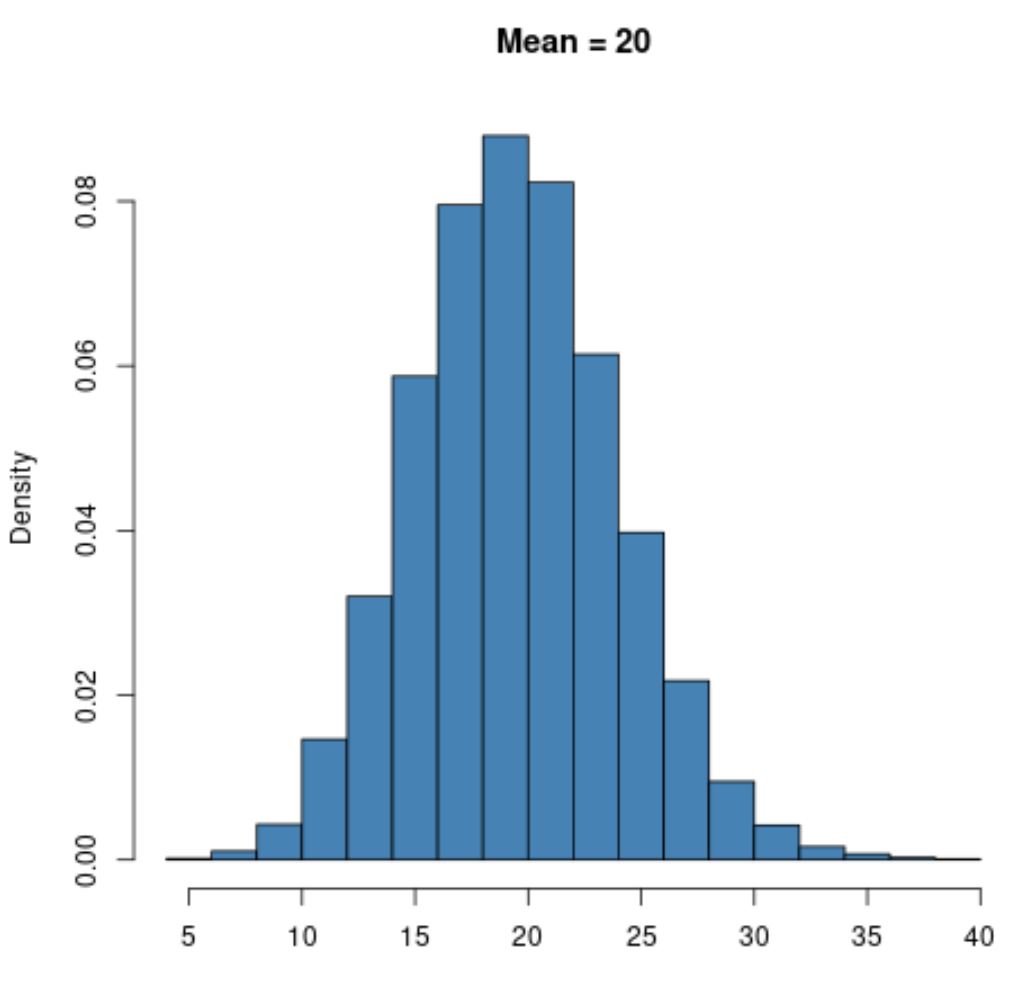
Należy pamiętać, że dolna granica rozkładu Poissona zawsze będzie wynosić zero, niezależnie od wartości średniej, ponieważ rozkładu Poissona można używać tylko z wartościami całkowitymi równymi lub większymi od zera.

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji na temat rozkładu Poissona:

Wprowadzenie do rozkładu Poissona
Cztery hipotezy rozkładu Poissona
5 konkretnych przykładów rozkładu Poissona

Poniższe samouczki zawierają dodatkowe informacje na temat rozkładu normalnego:

Wprowadzenie do rozkładu normalnego
6 konkretnych przykładów rozkładu normalnego
Generator zbioru danych o rozkładzie normalnym