Testowanie hipotez dotyczących proporcji
W tym artykule wyjaśniono, jaki udział w statystyce ma testowanie hipotez. Znajdziesz zatem wzór na sprawdzenie hipotezy proporcji oraz dodatkowo ćwiczenie krok po kroku pozwalające w pełni zrozumieć jak to się robi.
Na czym polega testowanie hipotez dotyczących proporcji?
Testowanie hipotezy proporcji to metoda statystyczna stosowana do określenia, czy odrzucić hipotezę zerową dotyczącą proporcji populacji.
Zatem w zależności od wartości statystyki testowej hipotezy dla proporcji i poziomu istotności hipoteza zerowa zostaje odrzucona lub przyjęta.
Należy pamiętać, że testowanie hipotez można również nazwać kontrastami hipotez, testowaniem hipotez lub testowaniem istotności.
Testowanie hipotezy Wzór na proporcję
Statystyka testu hipotezy dla proporcji jest równa różnicy proporcji próbki pomniejszonej o proponowaną wartość proporcji podzieloną przez odchylenie standardowe proporcji.
Wzór hipotezy testowej dla proporcji jest zatem następujący:

Złoto:
-

jest statystyką testującą hipotezę dla proporcji.
-

jest proporcją próbki.
-

jest wartością proponowanej proporcji.
-

to wielkość próbki.
-

jest odchyleniem standardowym proporcji.
Należy pamiętać, że nie wystarczy obliczyć statystykę testu hipotezy dla proporcji, ale wynik należy następnie zinterpretować:
- Jeżeli test hipotezy dla proporcji jest dwustronny, hipotezę zerową odrzuca się, jeśli wartość bezwzględna statystyki jest większa niż wartość krytyczna Z α/2 .
- Jeśli test hipotezy dla proporcji odpowiada prawemu ogonowi, hipoteza zerowa jest odrzucana, jeśli statystyka jest większa niż wartość krytyczna Z α .
- Jeśli test hipotezy dla proporcji odpowiada lewemu ogonowi, hipoteza zerowa jest odrzucana, jeśli statystyka jest mniejsza niż wartość krytyczna -Z α .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7d5bd583532769e3014286e8ffd94c9f_l3.png)
Pamiętaj, że wartości krytyczne można łatwo uzyskać z tabeli rozkładu normalnego.
Przykład testowania hipotezy dotyczącej proporcji
Kiedy już poznamy definicję testowania hipotez pod kątem proporcji i jaki jest jej wzór, rozwiążemy przykład, aby lepiej zrozumieć tę koncepcję.
- Według producenta lek na konkretną chorobę ma 70% skuteczności. W laboratorium testujemy skuteczność tego leku, ponieważ naukowcy uważają, że proporcja jest inna. W tym celu lek jest testowany na próbie 1000 pacjentów i 641 osób zostaje wyleczonych. Wykonaj test hipotezy na temat proporcji populacji z poziomem istotności 5%, aby odrzucić lub nie hipotezę badaczy.
W tym przypadku hipoteza zerowa i hipoteza alternatywna testu hipotezy dla proporcji populacji to:
![Rendered by QuickLaTeX.com \begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f7da8281eeecc022e2ec7daea6a9756e_l3.png)
Odsetek osób w próbie, które zostały wyleczone dzięki lekowi, wynosi:
![]()
Obliczamy statystykę testu hipotezy dla proporcji, stosując wzór pokazany powyżej:
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e689388b0a73e91c1e3d8812c2c4c42a_l3.png)
Z drugiej strony, ponieważ poziom istotności wynosi 0,05 i jest to test hipotezy dwustronnej, wartość krytyczna testu wynosi 1,96.
![]()
Podsumowując, wartość bezwzględna statystyki testowej jest większa od wartości krytycznej, dlatego odrzucamy hipotezę zerową i przyjmujemy hipotezę alternatywną.
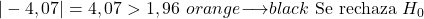 ➤ Zobacz: Testowanie hipotez dla średniej
➤ Zobacz: Testowanie hipotez dla średniej
Testowanie hipotez dla dwóch proporcji próbek
Testowanie hipotez dla proporcji dwóch próbek służy do odrzucenia lub przyjęcia hipotezy zerowej, że proporcje dwóch różnych populacji są równe.
Zatem hipoteza zerowa testu hipotezy dla proporcji dwóch próbek wynosi zawsze:
![]()
Hipotezą alternatywną może być jedna z trzech opcji:
*** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
Wzór na obliczenie statystyki testu hipotezy dla dwóch proporcji próbek to:
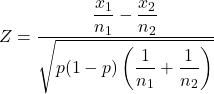
Złoto:
-

jest statystyką testową hipotezy dla proporcji dwóch próbek.
-
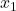
to liczba wyników w próbce 1.
-
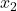
to liczba wyników w próbce 2.
-

to próbka o wielkości 1.
-

to próbka o wielkości 2.
-

jest łączną proporcją dwóch próbek.
Testowanie hipotez dla k proporcji próbek
Celem testu hipotezy dotyczącego proporcji k próbek jest ustalenie, czy wszystkie proporcje w różnych populacjach są równe, czy też przeciwnie, czy istnieją różne proporcje. Zatem hipoteza zerowa i hipoteza alternatywna w tym przypadku to:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-77d7e13b427dd927953473a6bfbe9a55_l3.png)
W takim przypadku łączną proporcję wszystkich próbek oblicza się w następujący sposób:
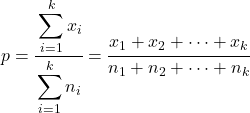
Wzór na znalezienie statystyki testu hipotezy dla k proporcji próbek to:
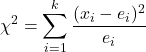
![]()
Złoto:
-

jest statystyką testową hipotezy dla k proporcji próbek. W tym przypadku statystyka ma rozkład chi-kwadrat.
-

to liczba wyników w próbce i.
-

to wielkość próbki, tj.
-

jest łączną proporcją wszystkich próbek.
-

to liczba oczekiwanych trafień z próbki i. Oblicza się go, mnożąc łączną proporcję

według wielkości próbki

.