Próbka średnia

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule dowiesz się, jaka jest średnia z próby w statystykach. Znajdziesz tu również sposób obliczenia średniej próbki, rozwiązane ćwiczenie, a ponadto kalkulator online umożliwiający obliczenie średniej dowolnej próbki.

Co oznacza próbka?

W statystyce średnia próbki jest średnią wartości w próbce. Aby obliczyć średnią próbki, należy dodać wszystkie wartości w próbce, a następnie podzielić przez całkowitą liczbę danych w próbce.

Symbolem środka próbki jest

$\overline{x}$

W badaniu statystycznym na ogół nie są znane wszystkie wartości populacji, dlatego wybiera się próbę populacji w celu jej analizy i ekstrapolacji uzyskanych wniosków na całą populację. Zatem średnia próbki służy do oszacowania średniej populacji.

Przykład formuły średniej

Średnia próbki jest równa sumie wartości wszystkich próbek podzielonej przez wielkość próbki. Oznacza to, że aby obliczyć średnią próbki, wszystkie wartości w próbce są dodawane, a następnie dzielone przez całkowitą liczbę danych w próbce.

Dlatego wzór na obliczenie średniej próbki jest następujący :

$\displaystyle\overline{x}=\frac{\displaystyle \sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+\dots +x_n}{n}$

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć średnią próbki dowolnego zbioru danych.

Należy pamiętać, że średnią próbki oblicza się na podstawie danych z próby, zatem wartość średniej populacji może różnić się od wartości obliczonej.

Przykładowy przykład obliczenia średniej

Teraz, gdy znamy już definicję średniej próbki i jej wzór, zobaczmy, jak uzyskać średnią próbki ze zbioru danych, rozwiązując prosty przykład.

Jose chce przeprowadzić się do centrum miasta, ale nie ma zbyt wiele czasu, więc nie może analizować cen wszystkich mieszkań do wynajęcia. Decydujesz się więc spojrzeć tylko na ceny wynajmu pięciu mieszkań (pokazane poniżej), aby dowiedzieć się, ile będzie Cię kosztować życie w centrum miasta. Jaka jest średnia cena próbki?

600 € 430 € 820 € 575 € 950

Aby znaleźć średnią z próbki, musimy dodać wszystkie wartości z próbki, a następnie podzielić przez całkowitą liczbę obserwacji, która wynosi 5. Stosujemy więc wzór na średnią z próbki:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+x_3+x_4+x_5}{n}$

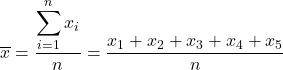
Następnie podstawiamy dane do wzoru i obliczamy średnią próbki:

$\overline{x}=\cfrac{600+430+820+575+950}{5}=675$

Krótko mówiąc, średnia cena wybranej do próby mieszkań wynosi 675 euro.

Przykład kalkulatora średniej

Wprowadź dane z dowolnej próbki statystycznej do poniższego kalkulatora, aby obliczyć średnią próbki. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

Średnia próbki i średnia populacji

Średnia populacji to średnia populacji statystycznej . Średnia populacji jest zatem średnią wszystkich elementów, na podstawie których zamierza się przeprowadzić badanie statystyczne.

Dlatego różnica między średnią próbki a średnią populacji polega na tym, że średnia próbki jest średnią wartości próbki, podczas gdy średnia populacji jest średnią wartości w populacji.

Aby odróżnić średnią próbki od średniej populacji, są one oznaczone różnymi symbolami. Symbolem środka próbki jest

$\overline{x}$

, podczas gdy symbolem oznaczającym populację jest

$\mu$

$\begin{array}{c}\overline{x} = \text{Media muestral}\\[2ex]\mu =\text{Media poblacional}\end{array}$

Średnia próbki służy do oszacowania wartości średniej populacji, czego można dokonać za pomocą estymacji punktowej lub estymacji przedziałowej .

➤ Zobacz: Jaka jest średnia populacji?

Rozkład próbkowania środków z próby

Na koniec przyjrzyjmy się, co oznacza rozkład próby, ponieważ jest to koncepcja statystyczna, która może być myląca.

Zacznijmy od zdefiniowania, czym jest rozkład próbkowania. Rozkład próby to rozkład będący wynikiem uwzględnienia wszystkich możliwych próbek z populacji statystycznej.

Zatem rozkład średniej próby jest rozkładem wynikającym z obliczenia średniej każdej możliwej próbki z populacji. Oznacza to, że jeśli przeanalizujemy wszystkie możliwe próbki z populacji i obliczymy średnią każdej z próbek, zestaw obliczonych wartości jest rozkładem próbkowania średniej próbki.

Podsumowując, choć średnia próby i rozkład próbkowania mają podobne nazwy, należy wiedzieć, jak je rozróżnić: średnia próby jest parametrem statystycznym, który jest obliczany z próby, natomiast rozkład próbkowania jest rozkładem wynika to z badania wszystkich próbek, jakie można pobrać z populacji.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej