Krytyczna wartość

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W artykule wyjaśniono, czym jest wartość krytyczna w statystyce i jak należy ją interpretować przy testowaniu hipotez. Podobnie będziesz mógł zobaczyć, jak obliczana jest wartość krytyczna, a także kilka konkretnych przykładów.

Co to jest wartość krytyczna?

Wartość krytyczna to punkt w rozkładzie statystyki testowej oddzielający obszar odrzucenia hipotezy zerowej od obszaru jej akceptacji. Innymi słowy, wartość krytyczna to wartość rozkładu testu statystycznego, który wyznacza granicę obszaru odrzucenia (lub obszaru krytycznego).

Zwykle wartość krytyczna jest reprezentowana przez symbol Z _α/2 , ponieważ najczęstszym rozkładem odniesienia jest zwykle standardowy rozkład normalny .

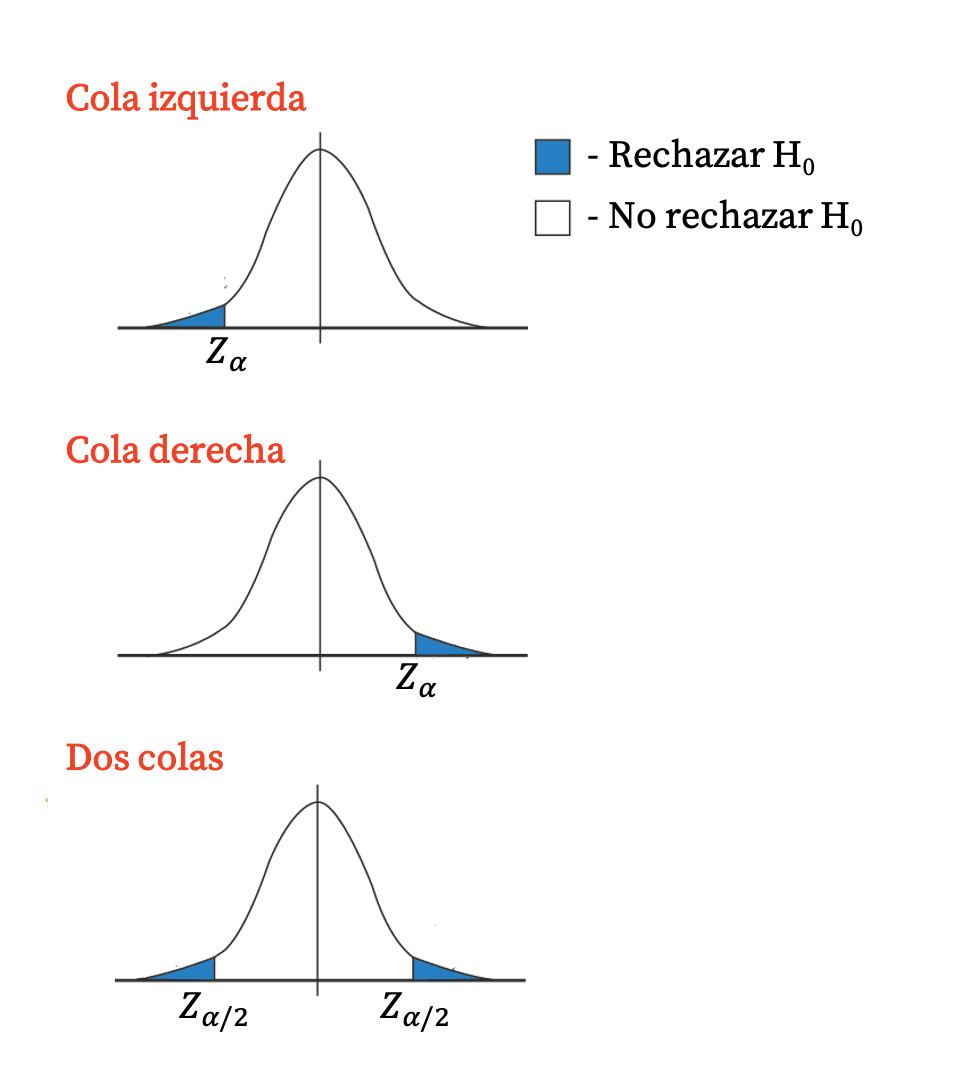
Ogólnie rzecz biorąc, testy jednostronne mają wartość krytyczną, ponieważ obszar odrzucenia stanowi pojedynczy ogon rozkładu. Z drugiej strony testy dwustronne mają dwie wartości krytyczne, ponieważ obszar odrzucenia odpowiada obu ogonom rozkładu.

W przedziałach ufności wartościami krytycznymi są punkty w rozkładzie odniesienia, które wyznaczają granice przedziału ufności.

Jak obliczyć wartość krytyczną

Zobaczymy wtedy, jak obliczane są najczęstsze wartości krytyczne. Wartość krytyczną Z i wartość krytyczną t oblicza się dla przedziału ufności średniej, jedyną różnicą jest to, że wartość krytyczną Z oblicza się, gdy znane jest odchylenie standardowe populacji, a zamiast tego stosuje się wartość krytyczną t gdy znane są tylko dane dla jednej próbki.

Wartość krytyczna Z

Wartość krytyczna Z służy do określenia granic przedziału ufności dla średniej. Mówiąc dokładniej, stosuje się go tylko wtedy, gdy znane jest odchylenie standardowe populacji.

Aby obliczyć wartość krytyczną Z, w tabeli standardowego rozkładu normalnego należy znaleźć wartość odpowiadającą prawdopodobieństwu połowy poziomu istotności.

Na przykład, jeśli chcemy wyznaczyć przedział ufności dla średniej przy poziomie ufności 95%, oznacza to, że poziom istotności wynosi 5%. Dlatego konieczne jest sprawdzenie w tabeli standardowego rozkładu normalnego, która wartość odpowiada prawdopodobieństwu 2,5%, ponieważ przedział ufności dla średniej jest dwustronny.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

Poniżej znajduje się tabela z najczęściej używanymi wartościami krytycznymi Z:

Poziom ufności (1-α)	Poziom istotności (α)	Wartość krytyczna (Z _α/2 )
0,80	0,20	1282
0,85	0,15	1440
0,90	0,10	1645
0,95	0,05	1960
0,99	0,01	2576
0,995	0,005	2807
0,999	0,001	3291

Wartość krytyczna t

Krytyczną wartość t wykorzystuje się do znalezienia granic przedziału ufności dla średniej, gdy odchylenie standardowe populacji jest nieznane.

Aby obliczyć wartość krytyczną t, w tabeli rozkładu t-Studenta należy znaleźć wartość odpowiadającą prawdopodobieństwu połowy poziomu istotności, biorąc pod uwagę, że stopnie swobody rozkładu t-Studenta są jednostkowe. niż wielkość próbki.

Na przykład, jeśli chcemy znaleźć przedział ufności przy poziomie ufności 95%, a wielkość próby wynosi 8, musimy uzyskać dostęp do tabeli rozkładu t-Studenta i zobaczyć, która wartość odpowiada t _0,025|7 .

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}$

➤ Zobacz: Jak obliczyć przedział ufności średniej

Wartość krytyczna w testowaniu hipotez

Wartość krytyczna może być również wykorzystana w testowaniu hipotez w celu odrzucenia hipotezy zerowej (i zaakceptowania hipotezy alternatywnej) lub odrzucenia hipotezy alternatywnej (i zaakceptowania hipotezy zerowej).

Jeżeli wartość rozkładu statystyki testowej odpowiadająca wartości p mieści się w przedziale wyznaczonym przez wartości krytyczne, nie odrzuca się hipotezy zerowej (odrzuca się hipotezę alternatywną).
Jeżeli wartość rozkładu statystyki testowej odpowiadająca wartości p znajduje się poza przedziałem wyznaczonym przez wartości krytyczne, hipotezę zerową odrzuca się (przyjmuje się hipotezę alternatywną).

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej