Próbkowanie rozkładu proporcji

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest rozkład proporcji próbkowania w statystyce. Znajdziesz tu także wzór na rozkład proporcjonalny próbki oraz dodatkowo rozwiązane ćwiczenie krok po kroku.

Jaki jest rozkład próbkowania tej proporcji?

Rozkład próbkowania proporcji (lub rozkład próbkowania proporcji ) to rozkład wynikający z obliczenia proporcji każdej możliwej próbki z populacji. Oznacza to, że proporcje próbkowania wszystkich możliwych próbek z populacji tworzą rozkład próbkowania tej proporcji.

Innymi słowy, proporcjonalny rozkład próbkowania uzyskuje się poprzez zbadanie wszystkich próbek, które można wybrać z populacji i wyprowadzenie proporcji próbkowania dla każdej próbki. Zatem zbiór obliczonych proporcji próby stanowi rozkład próbkowania proporcji.

Jeśli zastanawiasz się do czego służy rozkład proporcji w próbowaniu, w statystyce służy on do obliczania prawdopodobieństwa zbliżenia się do wartości proporcji populacji przy analizie pojedynczej próby.

➤ Patrz: Próbkowanie rozkładu średniej

Wzór na proporcjonalny rozkład próbkowania

Tak naprawdę, badając część próby, analizujemy przypadki sukcesu. Dlatego zmienna losowa w badaniu ma dwumianowy rozkład prawdopodobieństwa .

Zgodnie z centralnym twierdzeniem granicznym, dla dużych rozmiarów (n>30) możemy przybliżyć rozkład dwumianowy do rozkładu normalnego. Dlatego rozkład próbkowania proporcji jest zbliżony do rozkładu normalnego z następującymi parametrami:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Złoto

$p$

jest prawdopodobieństwem sukcesu i

$q$

jest prawdopodobieństwo niepowodzenia

$q=1-p$

Uwaga: Rozkład dwumianowy można przybliżyć do rozkładu normalnego tylko wtedy, gdy:

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”> , <p class=$ $np\ge 5$

$nq\ge 5$

➤ Zobacz: Przykłady rozkładów normalnych

Ponieważ zatem rozkład próbkowania tej proporcji można przybliżyć do rozkładu normalnego, wzór na obliczenie prawdopodobieństwa związanego z proporcją próbki jest następujący:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Złoto:

$\widehat{p}$

jest proporcją próbki.
$p$

jest odsetek populacji.
$q$

jest prawdopodobieństwem niepowodzenia populacji,

$q=1-p$

.
$n$

to wielkość próbki.
$Z$

jest zmienną zdefiniowaną przez standardowy rozkład normalny N(0,1).

Konkretny przykład proporcjonalnego rozkładu próbek

Po zapoznaniu się z definicją proporcjonalnego rozkładu próbkowania i związanymi z nim wzorami, poniżej znajduje się przykład rozwiązany krok po kroku, aby w pełni zrozumieć tę koncepcję.

Firma przemysłowa kupuje partie części od fabryki, która twierdzi, że produkuje części zawierające jedynie 3% wadliwych części. Aby to sprawdzić, firma postanawia przeanalizować zamówienie na 500 części. Jakie jest prawdopodobieństwo znalezienia w próbce więcej niż 5% wadliwych części?

W tym przypadku odsetek populacji, który chcemy zbadać, wynosi 0,03, więc parametr q jest równy 0,97.

$\begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}$

Aby więc znaleźć prawdopodobieństwo, że nas zapytają, musimy obliczyć odpowiednią statystykę, stosując wzór, który widzieliśmy w poprzedniej sekcji:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}=\cfrac{0,05-0,03}{\displaystyle\sqrt{\frac{0,03\cdot 0,97}{500}}}=2,62$

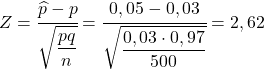
Zatem prawdopodobieństwo otrzymania więcej niż 5% wadliwych części jest równoważne następującemu prawdopodobieństwu:

$P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”360″ style=”vertical-align: -5px;”> Na koniec szukamy prawdopodobieństwa P[Z≤2,62] w <a href=$ tabeli rozkładu Z i obliczamy prawdopodobieństwo, że problem zadaje nam pytanie:

$\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=”Rendered by QuickLaTeX.com” height=”167″ width=”162″ style=”vertical-align: 0px;”> Podsumowując, prawdopodobieństwo znalezienia w analizowanej próbie więcej niż 5% wadliwych części wynosi 0,44%. </div>  <div class=$

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Jaki jest rozkład próbkowania tej proporcji?

Wzór na proporcjonalny rozkład próbkowania

Konkretny przykład proporcjonalnego rozkładu próbek

o autorze

Dr Benjamin Anderson

Dodaj komentarz