Przedział ufności dla różnicy średnich
W tym artykule wyjaśniono, czym jest przedział ufności dla różnicy średnich w statystykach i do czego się go stosuje. W ten sposób dowiesz się, jak obliczyć przedział ufności dla różnicy dwóch średnich i dowiesz się, jak krok po kroku rozwiązać ćwiczenie.
Jaki jest przedział ufności dla różnicy średnich?
Przedział ufności dla różnicy średnich to przedział zapewniający wartość maksymalną i minimalną, pomiędzy którymi wartość różnicy średnich dwóch populacji leży z pewnym poziomem ufności.
Na przykład, jeśli przedział ufności dla różnicy średnich dwóch populacji z 95% poziomem ufności wynosi (3,5), oznacza to, że różnica między średnimi obu populacji będzie wynosić od 3 do 5 z prawdopodobieństwem 95 %.
Dlatego w statystyce przedział ufności dla różnicy średnich służy do oszacowania dwóch wartości, pomiędzy którymi leży różnica między średnimi z dwóch populacji. Zatem wykorzystując dane z dwóch prób, możliwe jest przybliżenie różnicy pomiędzy średnimi populacji.
Wzór na przedział ufności dla różnicy średnich
Wzór na przedział ufności dla różnicy średnich zależy od tego, czy znane są wariancje populacji, a jeśli nie, to od tego, czy można założyć, że wariancje populacji są równe. . Zobaczymy wówczas, jak w każdym przypadku obliczany jest przedział ufności dla różnicy średnich.
znane odchylenia
Wzór na obliczenie przedziału ufności dla różnicy średnich, gdy znane są wariancje dwóch populacji przy poziomie ufności 1-α, jest następujący:
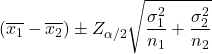
Złoto:
-

jest średnią próbki i.
-

jest odchyleniem standardowym populacji, tj.
-

jest wartością standardowego rozkładu normalnego z prawdopodobieństwem α/2.
-

to wielkość próbki, tj.
Ten przypadek jest najmniej powszechny, ponieważ wartość wariancji populacji jest generalnie nieznana.
nieznane i równe wariancje
Jeżeli wariancje obu populacji są nieznane, ale można je oszacować jako równe, wzór na obliczenie przedziału ufności dla różnicy średnich przy poziomie ufności 1-α jest następujący:
![]()
Złoto:
-

jest średnią próbki i.
-

jest zbiorczym odchyleniem standardowym.
-

jest wartością rozkładu t-Studenta n 1 + n 2 -2 stopni swobody z prawdopodobieństwem α/2.
-

to wielkość próbki, tj.
Ponieważ w tym przypadku zakłada się, że wariancje populacji są równoważne, do obliczenia przedziału ufności wykorzystuje się złożone odchylenie standardowe, które oblicza się ze wzoru:

Złoto
![]()
jest odchyleniem standardowym próbki i.
Nieznane i różne odmiany
Jeżeli wariancje obu populacji są nieznane i nie można założyć, że są równe, wzór na obliczenie przedziału ufności dla różnicy średnich przy poziomie ufności 1-α jest następujący:
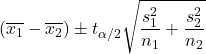
Złoto:
-

jest średnią próbki i.
-
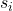
jest odchyleniem standardowym próbki i.
-

jest wartością rozkładu t-Studenta z prawdopodobieństwem α/2.
-

to wielkość próbki, tj.
W tym przypadku stopnie swobody rozkładu t-Studenta obliczane są ze wzoru:

Złoto
![]()
jest odchyleniem standardowym próbki i.
Konkretny przykład przedziału ufności dla różnicy średnich
Po zapoznaniu się z definicją przedziału ufności dla różnicy średnich i poznaniem różnych wzorów, zobaczymy teraz konkretny przykład pozwalający zakończyć przyswojenie sposobu obliczania przedziału ufności dla różnicy dwóch średnich.
- Chcemy zbadać wpływ tytoniu na masę urodzeniową dzieci. W tym celu porównuje się dwie próby: pierwszą próbę stanowią dzieci, których matki nie paliły, drugą próbę – dzieci, których matki paliły (parametry próby podano poniżej). Oblicz przedział ufności dla różnicy średnich przy poziomie ufności 95%.
- Matki niepalące:
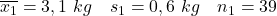
- Palące matki:
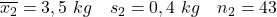
- Matki niepalące:
W tym przypadku nie znamy wartości wariancji populacji, możemy jednak założyć, że wariancje populacji są równoważne, ponieważ mamy do czynienia z dwiema populacjami o bardzo podobnych cechach. Zatem wzór na przedział ufności dla różnicy średnich, który powinniśmy zastosować, wygląda następująco:
![]()
W ten sposób obliczamy łączne odchylenie standardowe z odchyleń standardowych dwóch próbek:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
Podobnie musimy znaleźć wartość rozkładu t-Studenta 80 stopni swobody z prawdopodobieństwem 2,5% w tabeli rozkładu prawdopodobieństwa rozkładu t-Studenta :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
Na koniec podstawiamy dane do wzoru na przedział ufności dla różnicy średnich i wykonujemy obliczenia:
![]()
![]()
![]()
Przedział ufności dla różnicy środków problemu jest zatem następujący:
![]()