Dystrybucja próbek

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest rozkład próbkowania w statystyce i do czego się go używa. W ten sposób znajdziesz znaczenie rozkładu próbkowania, konkretny przykład rozkładu próbkowania, a ponadto wzory na najczęstsze typy rozkładów próbkowania.

Jaki jest rozkład próbkowania?

Rozkład próbkowania lub rozkład próbkowania to rozkład wynikający z uwzględnienia wszystkich możliwych próbek z populacji. Innymi słowy, rozkład próbkowania to rozkład uzyskany poprzez obliczenie parametru próbkowania wszystkich możliwych próbek z populacji.

Na przykład, jeśli wyodrębnimy wszystkie możliwe próbki z populacji statystycznej i obliczymy średnią każdej próbki, zbiór średnich z próby tworzy rozkład próbkowania. Dokładniej, ponieważ obliczony parametr jest średnią arytmetyczną, jest to rozkład średniej z próbkowania.

W statystyce rozkład próbkowania służy do obliczenia prawdopodobieństwa zbliżenia się do wartości parametru populacji podczas badania pojedynczej próby. Podobnie rozkład próbkowania pozwala oszacować błąd próbkowania dla danej liczebności próby.

Przykład rozkładu próbkowania

Teraz, gdy znamy definicję rozkładu próbkowania, spójrzmy na prosty przykład, aby w pełni zrozumieć tę koncepcję.

Do pudełka wkładamy trzy kule i na każdej z nich zapisana jest liczba od 1 do 3, tak aby jedna kula miała numer 1, druga kula miała numer 2, a ostatnia kula miała numer 3. Dla próbki o rozmiarze n = 2, oblicza prawdopodobieństwa rozkładu średniej w przypadku wybrania próbek z zastępowaniem.

Próbki wybierane są z wymianą, czyli kula zebrana w celu wybrania pierwszego elementu próbki wraca do pudełka i może zostać ponownie wybrana podczas drugiej ekstrakcji. Dlatego wszystkie możliwe próbki z populacji to:

1,1 1,2 1,3
2.1 2.2 2.3
3.1 3.2 3.3

W ten sposób obliczamy średnią arytmetyczną każdej możliwej próbki:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

Zatem prawdopodobieństwa uzyskania każdej wartości średniej próby przy wyborze próby losowej z populacji są następujące:

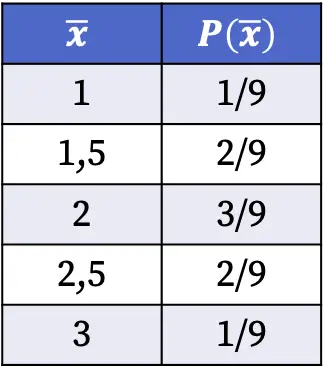
Prawdopodobieństwa rozkładu próbkowania pokazane w powyższej tabeli obliczono dzieląc liczbę próbek posiadających wspomnianą wartość średnią przez całkowitą liczbę możliwych przypadków. Na przykład: średnia próbki wynosi 1,5 w dwóch przypadkach na dziewięć możliwych, zatem P(1,5)=2/9.

Rodzaje rozkładów próbkowania

Rozkłady próbkowania (lub rozkłady próbkowania) można klasyfikować na podstawie parametru próbkowania, z którego zostały uzyskane. Zatem najczęstsze typy dystrybucji są następujące:

Rozkład średniej próby : Jest to rozkład próby wynikający z obliczenia średniej arytmetycznej każdej próbki.
Proporcjonalny rozkład próbkowania : Jest to rozkład próbkowania uzyskany poprzez obliczenie proporcji wszystkich próbek.
Rozkład wariancji próbkowania : jest to rozkład próbkowania, który tworzy zbiór wszystkich wariancji w próbie.
Różnica rozkładu średnich prób z dwóch różnych populacji.
Różnica w proporcjonalnym rozkładzie próbkowania : jest rozkładem próbkowania uzyskanym przez odjęcie wszystkich możliwych proporcji próbkowania z dwóch populacji.

Każdy rodzaj rozkładu próbkowania wyjaśniono bardziej szczegółowo poniżej.

Próbkowanie rozkładu średniej

Biorąc pod uwagę populację, która ma normalny rozkład prawdopodobieństwa ze średnią

$\mu$

i odchylenie standardowe

$\sigma$

i pobierane są próbki wielkości

$n$

, rozkład średniej próby będzie również określony rozkładem normalnym mającym następujące cechy:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Złoto

$\mu_{\overline{x}}$

jest średnią rozkładu próby średniej i

$\sigma_{\overline{x}}$

jest jego odchyleniem standardowym. Ponadto,

$\cfrac{\sigma}{\sqrt{n}}$

jest błędem standardowym rozkładu próbkowania.

Uwaga: Jeżeli populacja nie ma rozkładu normalnego, ale wielkość próby jest duża (n>30), rozkład średniej próby można również przybliżyć do powyższego rozkładu normalnego za pomocą granicy centralnego twierdzenia.

Dlatego też, ponieważ rozkład średniej z próby ma rozkład normalny, wzór na obliczenie prawdopodobieństwa związanego ze średnią z próbki jest następujący:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Złoto:

$\overline{x}$

to przykładowe środki.
$\mu$

To jest średnia populacji.
$s$

jest odchyleniem standardowym populacji.
$n$

to wielkość próbki.
$Z$

jest zmienną zdefiniowaną przez standardowy rozkład normalny N(0,1).

➤ Zobacz: Rozwiązane ćwiczenie dotyczące rozkładu próbkowania średniej

Próbkowanie rozkładu proporcji

Tak naprawdę, badając część próby, analizujemy przypadki sukcesu. Dlatego zmienna losowa w badaniu ma dwumianowy rozkład prawdopodobieństwa.

Zgodnie z centralnym twierdzeniem granicznym, dla dużych rozmiarów (n>30) możemy przybliżyć rozkład dwumianowy do rozkładu normalnego. Dlatego rozkład próbkowania proporcji jest zbliżony do rozkładu normalnego z następującymi parametrami:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Złoto

$p$

jest prawdopodobieństwem sukcesu i

$q$

jest prawdopodobieństwo niepowodzenia

$q=1-p$

Uwaga: Rozkład dwumianowy można przybliżyć do rozkładu normalnego tylko wtedy, gdy:

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”></p> <p> ,</p> <p class=$ $np\ge 5$

$nq\ge 5$

Ponieważ zatem rozkład próbkowania tej proporcji można przybliżyć do rozkładu normalnego, wzór na obliczenie prawdopodobieństwa związanego z proporcją próbki jest następujący:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Złoto:

$\widehat{p}$

jest proporcją próbki.
$p$

jest odsetek populacji.
$q$

jest prawdopodobieństwem niepowodzenia populacji,

$q=1-p$

.
$n$

to wielkość próbki.
$Z$

jest zmienną zdefiniowaną przez standardowy rozkład normalny N(0,1).

➤ Zobacz: Rozwiązane ćwiczenie dotyczące rozkładu próbkowania proporcji

Próbkowanie Rozkład wariancji

Rozkład wariancji próbkowania jest zdefiniowany przez rozkład prawdopodobieństwa chi-kwadrat. Dlatego wzór na statystykę rozkładu wariancji z próby jest następujący:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Złoto:

$\chi^2$

jest statystyką rozkładu wariancji z próbkowania, która jest zgodna z rozkładem chi-kwadrat.
$n$

to wielkość próbki.
$s^2$

jest wariancją próbki.
$\sigma^2$

jest wariancją populacji.

➤ Zobacz: Rozwiązane ćwiczenie dotyczące rozkładu próbkowania wariancji

Próbkowanie rozkładu różnicy średnich

Jeżeli wielkość próby jest wystarczająco duża (n ₁ ≥30 i n ₂ ≥30), rozkład średniej różnicy w próbce jest zgodny z rozkładem normalnym. Dokładniej, parametry wspomnianego rozkładu oblicza się w następujący sposób:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Uwaga: Jeżeli obie populacje mają rozkłady normalne, wówczas rozkład różnicy średnich w próbce jest zgodny z rozkładem normalnym niezależnie od wielkości próby.

Dlatego też, ponieważ rozkład próbkowania różnicy średnich jest określony przez rozkład normalny, wzór na obliczenie statystyki rozkładu próbkowania różnicy średnich jest następujący:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Złoto:

$\overline{x_i}$

jest średnią próbki i.
$\mu_i$

jest średnią populacji, tj.
$\sigma_i$

jest odchyleniem standardowym populacji, tj.
$n_i$

to wielkość próbki, tj.
$Z$

jest zmienną zdefiniowaną przez standardowy rozkład normalny N(0,1).

Należy pamiętać, że próbki z różnych populacji mogą mieć różną wielkość próby.

➤ Zobacz: Rozwiązane ćwiczenie dotyczące rozkładu próbkowania różnicy średnich

Próbkowanie rozkładu różnicy proporcji

Próby wybrane do różnicy proporcji rozkładu próbkowania są definiowane przez rozkłady dwumianowe, ponieważ dla celów praktycznych proporcja jest stosunkiem przypadków zakończonych sukcesem do całkowitej liczby obserwacji.

Jednakże, dzięki centralnemu twierdzeniu granicznemu, rozkłady dwumianowe można aproksymować do normalnych rozkładów prawdopodobieństwa. Dlatego rozkład próbkowania różnicy proporcji można przybliżyć do rozkładu normalnego o następujących cechach:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Uwaga: Rozkład próbkowania różnicy proporcji można przybliżyć do rozkładu normalnego tylko wtedy, gdy:

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

$n_2q_2\geq5$

Ponieważ zatem rozkład próbkowania różnicy proporcji można przybliżyć do rozkładu normalnego, wzór na obliczenie statystyki rozkładu próbkowania różnicy proporcji jest następujący:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

Złoto:

$\widehat{p_i}$

jest proporcją próbki, tj.
$p_i$

to odsetek populacji, tj.
$q_i$

jest prawdopodobieństwem niepowodzenia populacji i,

$q_i=1-p_i$

.
$n_i$

to wielkość próbki, tj.
$Z$

jest zmienną zdefiniowaną przez standardowy rozkład normalny N(0,1).

➤ Zobacz: Rozwiązane ćwiczenie dotyczące rozkładu próbkowania różnicy proporcji

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Jaki jest rozkład próbkowania?

Przykład rozkładu próbkowania

Rodzaje rozkładów próbkowania

Próbkowanie rozkładu średniej

Próbkowanie rozkładu proporcji

Próbkowanie Rozkład wariancji

Próbkowanie rozkładu różnicy średnich

Próbkowanie rozkładu różnicy proporcji

o autorze

Dr Benjamin Anderson

Dodaj komentarz