Znaczenie statystyki w edukacji (z przykładami)

Dziedzina statystyki zajmuje się gromadzeniem, analizą, interpretacją i prezentacją danych.

W kontekście edukacyjnym statystyki są ważne z następujących powodów:

Powód 1 : Statystyki pozwalają nauczycielom zrozumieć wyniki uczniów za pomocą statystyk opisowych.

Powód 2 : Statystyki pozwalają nauczycielom dostrzec trendy w wynikach uczniów za pomocą wizualizacji danych.

Powód 3 : Statystyka umożliwia nauczycielom porównywanie różnych metod nauczania za pomocą testowania hipotez.

W pozostałej części tego artykułu omówimy każdy z tych powodów.

Powód 1: Zrozum wyniki uczniów za pomocą statystyk opisowych

Statystyki opisowe służą do opisu danych.

W kontekście edukacyjnym nauczyciel może obliczyć następujące statystyki opisowe dla uczniów w swojej klasie:

• Średni wynik z danego egzaminu.
• Odchylenie standardowe wyników z określonego egzaminu.
• Zakres wyników na danym egzaminie.
• Odsetek uczniów, którzy zdali określony egzamin.
• 90. percentyl wyników na danym egzaminie.

Dzięki tym pomiarom nauczyciel może lepiej zrozumieć wyniki uczniów w swojej klasie na danym egzaminie.

Może wówczas zdecydować, czy zmienić metodę nauczania, jeśli zbyt mało uczniów zda egzamin, czy też zaoferować dodatkowe możliwości korepetycji uczniom, którzy uzyskują słabe wyniki na egzaminach itp.

Uwaga : tego typu statystyki opisowe stosowane są na wszystkich poziomach edukacji. Na przykład dyrektor może używać statystyk opisowych do monitorowania wyników uczniów w testach w całej szkole. Stanowy departament edukacji może również wykorzystywać statystyki opisowe do monitorowania wyników testów uczniów w całym stanie.

Powód 2: Wykrywaj trendy za pomocą wizualizacji danych

Innym powszechnym sposobem wykorzystania statystyki w edukacji jest wizualizacja danych, takich jak wykresy liniowe, histogramy, wykresy pudełkowe, wykresy kołowe i inne wykresy.

Tego typu wykresy są często używane, aby pomóc nauczycielom dostrzec trendy w wynikach zajęć i osiągnięć poszczególnych uczniów.

Załóżmy na przykład, że nauczyciel tworzy następujący wykres słupkowy, aby zwizualizować średni wynik egzaminu w ciągu roku:

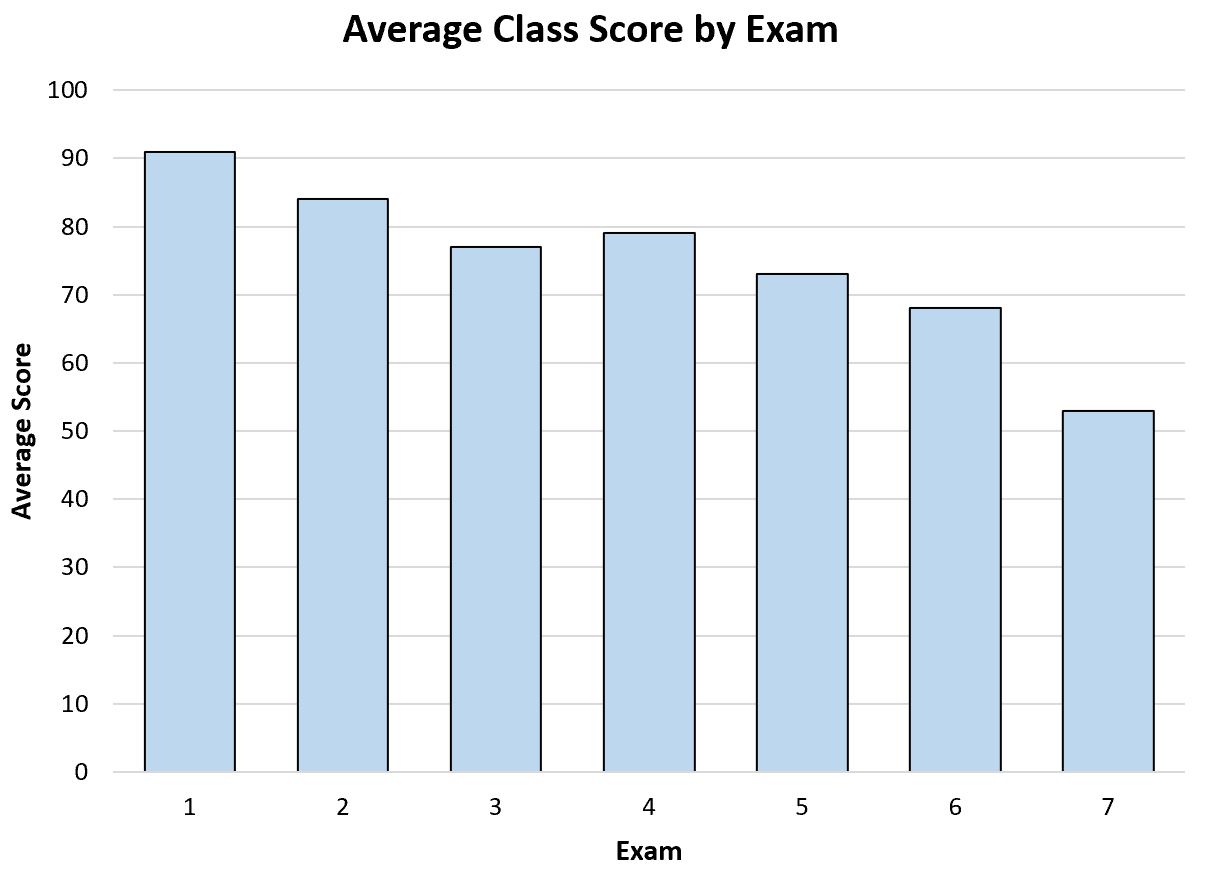
Wystarczy spojrzeć na ten wykres słupkowy, aby nauczyciel mógł zobaczyć, że średni wynik uczniów w ich klasie na testach powoli spada w ciągu roku.

Może to pozwolić nauczycielowi na udoskonalenie swoich metod nauczania lub być może przeprowadzić wśród uczniów ankietę, w której będą mogli zapytać o opinię na temat jego metod nauczania itp.

Powód 3: Porównaj metody nauczania za pomocą testowania hipotez

Statystyka jest również wykorzystywana w edukacji w formie testowania hipotez .

Są to testy, które nauczyciele mogą wykorzystać do ustalenia, czy istnieje statystyczna istotność pomiędzy różnymi metodami nauczania.

Załóżmy na przykład, że nauczyciel chce ustalić, czy określony program nauczania wpływa na wyniki testów. Aby to sprawdzić, losowo wybiera 15 uczniów, którzy przystępują do testu wstępnego. Następnie każe każdemu uczniowi korzystać z programu nauczania przez miesiąc, a następnie rozwiązuje test końcowy o podobnym stopniu trudności.

Wyniki testów każdego z 15 uczniów przedstawiono poniżej:

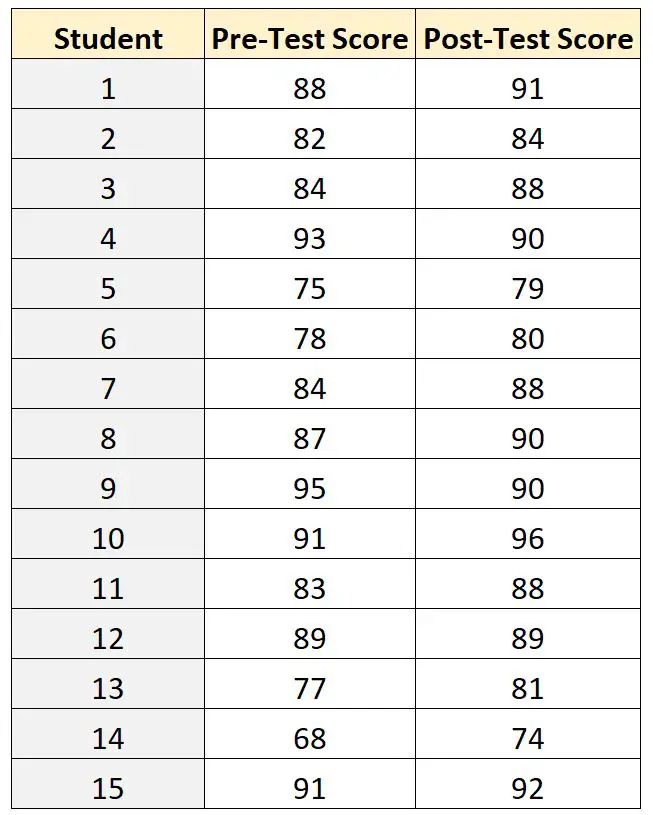
Aby porównać różnicę między średnimi wynikami przed testem i po teście, nauczyciel może zastosować sparowane próbki w teście t , ponieważ w przypadku każdego ucznia jego wynik przed testem można powiązać z wynikiem po teście.

Załóżmy, że profesor używa oprogramowania statystycznego do wykonania testu t dla par prób i otrzymuje następujące wyniki:

• Statystyka testu t: -2,97
• Wartość p: 0,0101

W tym przykładzie test t dla sparowanych próbek wykorzystuje następujące hipotezy zerowe i alternatywne:

• H ₀ : Średnie wyniki przed i po teście są równe
• H _A : Średnie wyniki przed i po teście nie są równe

Ponieważ wartość p ( 0,0101 ) jest mniejsza niż 0,05, odrzucamy hipotezę zerową.

Oznacza to, że mamy wystarczające dowody, aby stwierdzić, że średni wynik testu różni się w przypadku studentów przed i po wzięciu udziału w programie studiów.

Uwaga : to tylko jeden przykład testowania hipotez stosowany w edukacji. Inne popularne testy obejmują test t dla jednej próbki , test t dla dwóch próbek , jednoczynnikową ANOVA i dwuczynnikową ANOVA .

Dodatkowe zasoby

Poniższe artykuły wyjaśniają znaczenie statystyki w innych dziedzinach:

Znaczenie statystyki w przedsiębiorstwach
Znaczenie statystyki w ekonomii
Znaczenie statystyki w ochronie zdrowia