Współczynnik determinacji (r kwadrat)

Przez Benjamin Anderson 2 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, jaki jest współczynnik determinacji (lub R kwadrat) w statystyce. Dowiesz się więc, jak obliczyć współczynnik determinacji, jak go interpretować, a ponadto znajdziesz kalkulator online umożliwiający obliczenie współczynnika determinacji próbki danych.

Jaki jest współczynnik determinacji (R do kwadratu)?

Współczynnik determinacji , którego symbol to ^R2 ( R do kwadratu ), jest statystyką mierzącą dobroć dopasowania modelu regresji. Współczynnik determinacji pokazuje, jak dobrze model regresji pasuje do zbioru danych, to znaczy wskazuje procent wyjaśniony przez model regresji.

Zatem im wyższy współczynnik determinacji, tym lepszy model regresji. Choć warunek ten nie zawsze jest spełniony, w zasadzie interesuje nas jak największy współczynnik determinacji. Poniżej zobaczymy jak interpretować współczynnik determinacji.

Wzór wyznaczania współczynnika

Współczynnik determinacji jest równy jeden minus stosunek wariancji resztowej do wariancji zmiennej zależnej. Współczynnik determinacji można również obliczyć odejmując jeden minus suma kwadratów od reszt z całkowitej sumy kwadratów.

Zatem wzór na obliczenie współczynnika determinacji jest następujący:

wzór na współczynnik determinacji, wzór na r kwadrat

Złoto:

$R^2$

jest współczynnikiem determinacji.
$\sigma_r^2$

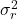
jest wariancją resztową.
$\sigma^2$

jest wariancją zmiennej zależnej Y.
$y_{i}$

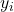
jest wartością zmiennej zależnej od obserwacji, tj.
$\widehat{y}_{i}$

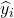
jest wartością przybliżoną przez model regresji dla obserwacji, tj.
$\overline{y}$

jest średnią zmiennej zależnej ze wszystkich obserwacji.

👉 Za pomocą poniższego kalkulatora możesz obliczyć współczynnik determinacji dla dowolnego zbioru danych.

W przypadku modelu regresji liniowej współczynnik determinacji jest równy kwadratowi współczynnika korelacji :

$R^2=\cfrac{\sigma_{XY}^2}{\sigma_X^2\sigma_Y^2}=\rho^2$

Złoto

$\sigma_{XY}^2$

jest kowariancją zmiennych X i Y,

$\sigma_X^2$

$\sigma_Y^2$

są wariancjami odpowiednio zmiennej niezależnej X i zmiennej zależnej Y.

Kalkulator współczynnika determinacji

Podłącz przykładowe dane do poniższego kalkulatora, aby dopasować prosty model regresji liniowej i obliczyć jego współczynnik determinacji. Należy rozdzielić pary danych tak, aby w pierwszym polu znajdowały się tylko wartości zmiennej niezależnej X, a w drugim polu znajdowały się wyłącznie wartości zmiennej zależnej Y.

Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

Interpretacja współczynnika determinacji

W tej sekcji zobaczymy, jak interpretować współczynnik determinacji, ponieważ nie ma sensu znać wartości współczynnika determinacji, jeśli nie będziesz wiedział później, co on oznacza.

Wartość współczynnika determinacji może wynosić od 0 do 1, jednak najczęściej wyrażana jest w procentach, zatem minimalna wartość wynosi 0%, a maksymalna 100%.

Jeśli chodzi o interpretację współczynnika determinacji , im wyższa jego wartość, tym oznacza, że model regresji lepiej wyjaśnia próbkę danych. Zatem im współczynnik determinacji jest bliższy 1, tym bardziej model będzie dostosowany. Z drugiej strony, im bliżej 0, tym mniej wiarygodny będzie utworzony model regresji.

Jednak przy porównywaniu dwóch modeli regresji nie zawsze model o wyższym współczynniku regresji jest lepszy. Przykładowo model regresji może mieć współczynnik regresji R ² = 100%, ponieważ do modelu dodano wiele zmiennych objaśniających, dzięki czemu może doskonale wyjaśnić wszystkie obserwacje. Jednak model ten z pewnością bardzo słabo przewiduje nową wartość, która nie została wykorzystana do zbudowania modelu regresji.

Należy także pamiętać, że powstały model regresji spełnia poprzednie założenia. Zatem model o bardzo wysokim współczynniku determinacji jest bezużyteczny, jeśli zmienność jego reszt nie jest stała (homoscedastyczność).

Ponadto współczynnik determinacji stanowi istotne ograniczenie, ponieważ nie penalizuje włączenia zmiennych objaśniających. Logicznie rzecz biorąc, im więcej zmiennych objaśniających ma model regresji, tym bardziej złożony będzie model, ale tym lepiej wyjaśni obserwowane dane, a zatem tym wyższy współczynnik determinacji. Skorygowany współczynnik determinacji uwzględnia jednak liczbę zmiennych w modelu (zobaczymy, jak to jest wyliczone poniżej).

Podsumowując, współczynnik determinacji jest bardzo przydatny do analizy modelu regresji, ponieważ pozwala nam dowiedzieć się, jak dobrze model regresji pasuje do zbioru danych. Do przeglądu powstałego modelu należy jednak zastosować także inne narzędzia, takie jak wykresy statystyczne .

Skorygowany współczynnik determinacji

Skorygowany współczynnik determinacji , zwany także skorygowanym współczynnikiem determinacji , mierzy stopień dopasowania modelu regresji, biorąc pod uwagę liczbę zmiennych objaśniających zawartych w modelu.

Różnica między współczynnikiem determinacji a skorygowanym współczynnikiem determinacji polega na tym, że współczynnik determinacji mierzy jakość dostosowania bez uwzględnienia liczby zmiennych, natomiast skorygowany współczynnik determinacji mierzy jakość dostosowania karanie za każdą dodaną zmienną.

Wzór na obliczenie skorygowanego współczynnika determinacji jest następujący:

$\bar{R}^2=1-\cfrac{N-1}{N-k-1}\cdot (1-R^2)$

Złoto:

$\bar{R}^2$

jest skorygowanym współczynnikiem determinacji.
$R^2$

jest współczynnikiem determinacji.
$N$

to wielkość próbki.
$k$

jest liczbą zmiennych objaśniających w modelu regresji.

Zatem skorygowany współczynnik determinacji jest lepszy niż współczynnik determinacji dla porównania dwóch różnych modeli, gdyż modele mogą mieć różną liczbę zmiennych objaśniających.

➤ Patrz: Skorygowany współczynnik determinacji

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej