Regresja logistyczna

Przez Benjamin Anderson 2 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest regresja logistyczna w statystyce. Podobnie znajdziesz wzór na regresję logistyczną, jakie są różne rodzaje regresji logistycznej, a ponadto rozwiązane ćwiczenie regresji logistycznej.

Co to jest regresja logistyczna?

W statystyce regresja logistyczna jest rodzajem modelu regresji używanego do przewidywania wyniku zmiennej kategorycznej . Oznacza to, że regresja logistyczna służy do modelowania prawdopodobieństwa, że zmienna kategoryczna przyjmie określoną wartość na podstawie zmiennych niezależnych.

Najpopularniejszym modelem regresji logistycznej jest binarna regresja logistyczna, w której istnieją tylko dwa możliwe wyniki: „porażka” lub „sukces” ( rozkład Bernoulliego ). „Porażka” jest reprezentowana przez wartość 0, natomiast „sukces” jest reprezentowany przez wartość 1.

Na przykład prawdopodobieństwo zdania egzaminu przez ucznia na podstawie godzin spędzonych na nauce można zbadać za pomocą modelu regresji logistycznej. W tym przypadku porażka byłaby wynikiem „porażki”, a z drugiej strony sukces byłby wynikiem „sukcesu”.

Formuła regresji logistycznej

Równanie modelu regresji logistycznej wygląda następująco:

$\displaystyle \ln \left(\frac{p}{1-p}\right) =\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i$

Dlatego w modelu regresji logistycznej prawdopodobieństwo uzyskania wyniku „sukcesu”, czyli przyjęcia przez zmienną zależną wartości 1, oblicza się ze wzoru:

$p=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}$

Złoto:

$p$

jest prawdopodobieństwem, że zmienna zależna wynosi 1.
$\beta_0$

jest stałą modelu regresji logistycznej.
$\beta_i$

jest współczynnikiem regresji zmiennej i.
$x_i$

jest wartością zmiennej i.

Przykład modelu regresji logistycznej

Teraz, gdy znamy już definicję regresji logistycznej, przyjrzyjmy się konkretnemu przykładowi, jak stworzyć model tego typu regresji.

W poniższej tabeli zestawiono serię 20 danych, które dotyczą godzin nauki każdego studenta oraz tego, czy zdał on, czy nie zdał egzamin statystyczny. Uruchom model regresji logistycznej i oblicz prawdopodobieństwo, że uczeń zaliczy egzamin, jeśli będzie się uczył przez 4 godziny.

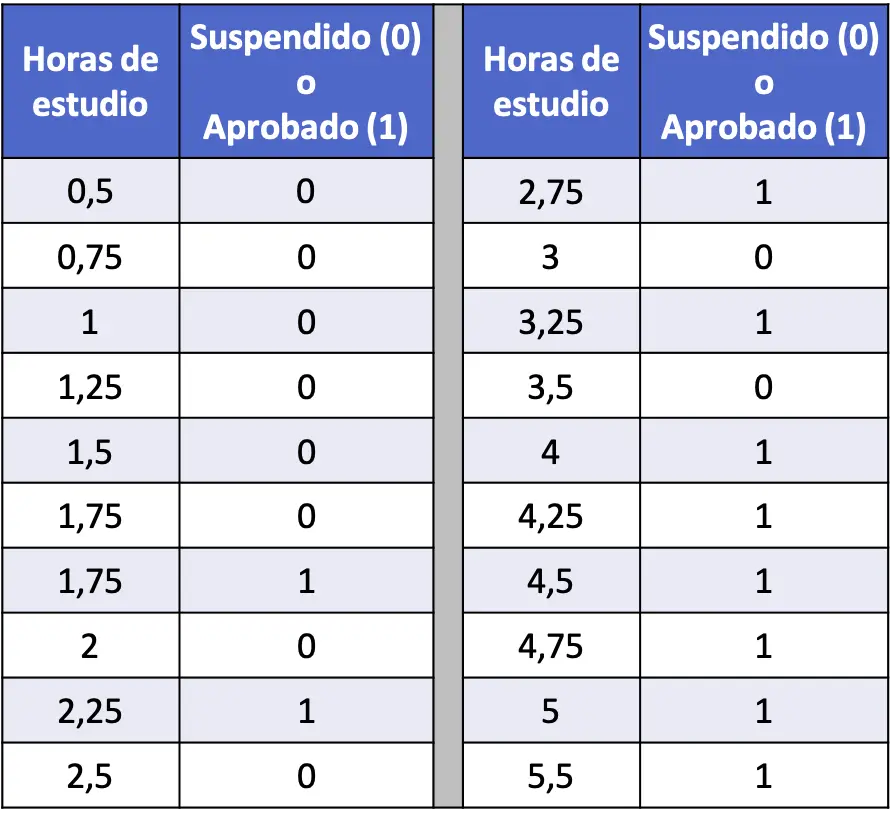
W tym przypadku zmienną objaśniającą jest liczba godzin nauki, a zmienną odpowiedzi jest to, czy student nie zaliczył (0), czy zdał (1). Dlatego w naszym modelu będziemy mieli tylko współczynnik

$\beta_0$

i współczynnik

$\beta_1$

, ponieważ istnieje tylko jedna zmienna niezależna.

$\beta_0 \qquad \beta_1$

Ręczne wyznaczanie współczynników regresji jest bardzo pracochłonne, dlatego zaleca się wykorzystanie oprogramowania komputerowego typu Minitab. Zatem wartości współczynników regresji obliczonych za pomocą programu Minitab przedstawiają się następująco:

$\begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}$

Model regresji logistycznej wygląda zatem następująco:

$\begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}$

Poniżej możesz zobaczyć przykładowe dane i wykres równania modelu regresji logistycznej:

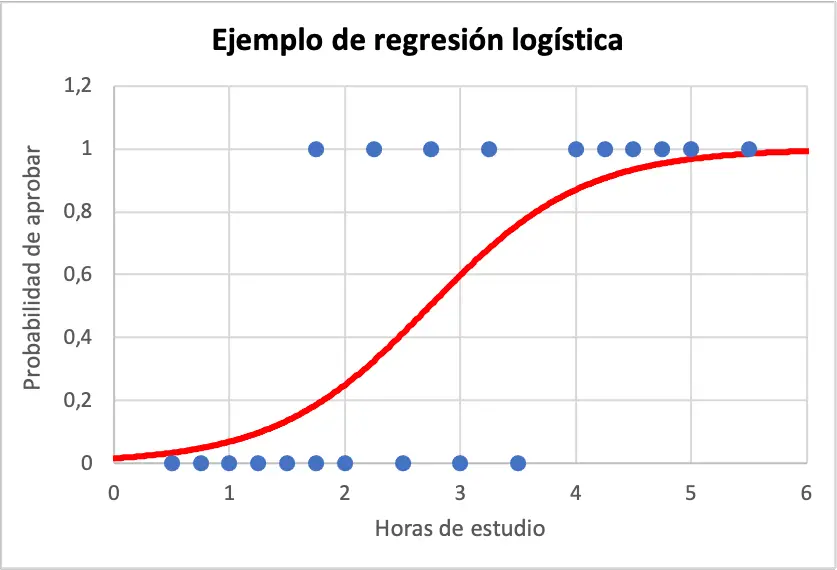
Zatem, aby obliczyć prawdopodobieństwo, że student odniesie sukces, jeśli przerobił 4 godziny, wystarczy skorzystać z równania uzyskanego z modelu regresji logistycznej:

$\begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}$

Krótko mówiąc, jeśli student uczy się cztery godziny, prawdopodobieństwo zdania egzaminu wynosi 86,99%.

Rodzaje regresji logistycznej

Wyróżnia się trzy rodzaje regresji logistycznej :

Binarna regresja logistyczna : Zmienna zależna może mieć tylko dwie wartości (0 i 1).
Wielomianowa regresja logistyczna : zmienna zależna ma więcej niż dwie możliwe wartości.
Porządkowa regresja logistyczna : możliwe wyniki mają naturalny porządek.

Regresja logistyczna i regresja liniowa

Na koniec, podsumowując, zobaczymy, jaka jest różnica między regresją logistyczną a regresją liniową, ponieważ najczęściej używanym modelem regresji w statystyce jest model liniowy.

Regresja liniowa służy do modelowania liczbowych zmiennych zależnych. Dodatkowo w regresji liniowej związek pomiędzy zmiennymi objaśniającymi a zmienną odpowiedzi jest liniowy.

Dlatego główną różnicą między regresją logistyczną a regresją liniową jest rodzaj zmiennej zależnej. W regresji logistycznej zmienna zależna ma charakter jakościowy, natomiast w regresji liniowej zmienna zależna ma charakter liczbowy.

Zatem regresja logistyczna służy do przewidywania wyniku pomiędzy dwiema możliwymi opcjami, podczas gdy regresja liniowa pomaga przewidzieć wynik liczbowy.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej