Linia regresji

Przez Benjamin Anderson 2 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest linia regresji w statystyce. Znajdziesz więc sposób obliczenia linii regresji pomiędzy dwiema zmiennymi, rozwiązane ćwiczenie oraz dodatkowo kalkulator online umożliwiający obliczenie linii regresji dla dowolnej próbki danych.

Jaka jest linia regresji?

W statystyce linią regresji jest linia uzyskana z prostego modelu regresji liniowej . Mówiąc dokładniej, linia regresji to linia, która najlepiej pasuje do wykresu punktowego i dlatego najlepiej opisuje zbiór danych statystycznych.

Zatem równanie linii regresji matematycznie wiąże zmienną niezależną X i zmienną zależną Y zbioru danych. Chociaż linia regresji na ogół nie jest w stanie precyzyjnie określić wartości każdej obserwacji, może zapewnić przybliżenie jej wartości.

Jak widać na poprzednim wykresie, linia regresji pomaga nam zobaczyć trend zbioru danych oraz rodzaj związku pomiędzy zmienną niezależną a zmienną zależną. Poniżej przyjrzymy się zastosowaniom linii regresji.

Wzór na linię regresji

Teraz, gdy znamy definicję linii regresji, zobaczmy, jak obliczyć równanie linii modelu regresji liniowej.

Jak każda prosta, równanie linii regresji składa się ze stałej (b ₀ ) i nachylenia (b ₁ ):

$y=b_0+b_1x$

Zatem wzory na obliczenie współczynników linii regresji liniowej są następujące:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}$

Złoto:

$b_0$

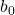
jest stałą linii regresji.
$b_1$

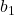
jest nachyleniem linii regresji.
$x_i$

jest wartością zmiennej niezależnej X danych i.
$y_i$

jest wartością zmiennej zależnej Y danych i.
$\overline{x}$

jest średnią wartości zmiennej niezależnej
$\overline{y}$

jest średnią wartości zmiennej zależnej Y.

👉 Za pomocą poniższego kalkulatora możesz obliczyć linię regresji dla dowolnego zbioru danych.

Konkretny przykład linii regresji

Aby dokładniej zbadać koncepcję linii regresji, poniżej znajduje się praktyczny przykład tworzenia linii regresji.

Po zdaniu egzaminu statystycznego pięciu studentów zostało zapytanych, ile godzin nauki spędzili na egzaminie, dane przedstawia poniższa tabela. Na podstawie zebranych danych statystycznych oblicz linię regresji, aby liniowo powiązać liczbę godzin nauki z uzyskaną oceną. Następnie ustal, jaką ocenę otrzyma uczeń, który uczył się 8 godzin.

Aby znaleźć linię regresji dla przykładowych danych, musimy wyznaczyć współczynniki b ₀ i b ₁ równania i w tym celu skorzystać ze wzorów przedstawionych w powyższej sekcji.

Aby jednak zastosować wzory na prostą regresji liniowej, musimy najpierw obliczyć średnią zmiennej niezależnej i średnią zmiennej zależnej:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Teraz, gdy znamy średnie zmiennych, obliczamy współczynnik b ₁ modelu, korzystając z odpowiedniego wzoru:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Na koniec obliczamy współczynnik b ₀ modelu, korzystając z odpowiedniego wzoru:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

Krótko mówiąc, równanie linii regresji liniowej problemu wygląda następująco:

$y=2,0294+0,4412x$

Poniżej możesz zobaczyć graficzną reprezentację przykładowych danych, a także linię prostą prostego modelu regresji liniowej:

Po obliczeniu linii regresji, aby przewidzieć ocenę, jaką uzyska student, który uczył się 8 godzin, wystarczy podstawić tę wartość do równania otrzymanej linii regresji:

$y=2,0294+0,4412\cdot 8=5,56$

Zatem zgodnie z przeprowadzonym modelem regresji liniowej, jeśli student uczył się osiem godzin, uzyska na egzaminie notę 5,56.

Do czego służy linia regresji?

Zasadniczo linia regresji ma dwa zastosowania: linia regresji służy do określenia rodzaju związku pomiędzy dwiema zmiennymi, a z drugiej strony linia regresji pozwala również na przewidywanie wartości nowej obserwacji.

Nachylenie linii regresji mówi nam, jaka jest korelacja między zmienną niezależną a zmienną zależną. Jeśli nachylenie jest dodatnie, oznacza to, że zmienna zależna jest wprost proporcjonalna do zmiennej niezależnej, natomiast jeśli nachylenie jest ujemne, oznacza to, że zmienne są odwrotnie proporcjonalne. Wreszcie, jeśli współczynnik nachylenia jest bardzo bliski zeru, oznacza to, że korelacja między dwiema zmiennymi jest bardzo słaba.

Dodatkowo, jeśli znane jest równanie prostej regresji, można przewidzieć wartość zmiennej zależnej dla nowej wartości zmiennej niezależnej, tak jak to zrobiliśmy w powyższym przykładzie. Zatem im lepiej dostosowana jest linia regresji, tym lepsze będą przewidywania.

Kalkulator linii regresji

Wprowadź próbkę danych do poniższego kalkulatora, aby obliczyć linię regresji między dwiema zmiennymi. Należy rozdzielić pary danych tak, aby w pierwszym polu znajdowały się tylko wartości zmiennej niezależnej X, a w drugim polu znajdowały się jedynie wartości zmiennej zależnej Y.

Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej