Jakość dopasowania
W tym artykule wyjaśniono, czym jest dobroć dopasowania w statystykach. Podobnie pokazuje, jak mierzyć dobroć dopasowania modelu regresji, a ponadto będzie można zobaczyć rozwiązane ćwiczenie dobroci dopasowania.
Czym jest dobroć dopasowania?
W statystyce dobroć dopasowania określa stopień dopasowania modelu regresji do próbki danych. Innymi słowy, dobroć dopasowania modelu regresji odnosi się do poziomu sprzężenia między zbiorem obserwacji a wartościami uzyskanymi w wyniku regresji.
Zatem im lepsze dopasowanie modelu regresji, tym lepiej wyjaśnia on badane dane. Zależy nam zatem na lepszym dopasowaniu modelu statystycznego, tym lepiej.
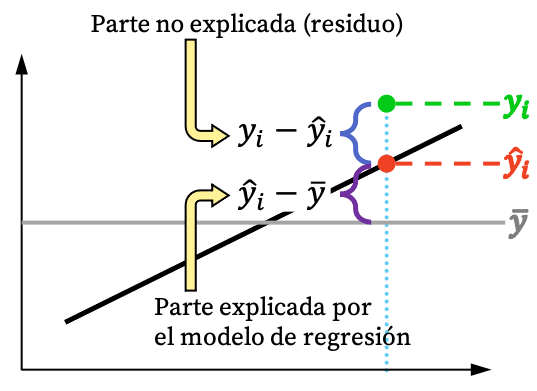
Jak widać na powyższym obrazku, wartości obserwacji zwykle nie można w pełni wyjaśnić za pomocą modelu regresji. Logicznie rzecz biorąc, im więcej model regresji może wyjaśnić na podstawie zbioru danych, tym lepiej będzie pasował. Krótko mówiąc, interesuje nas możliwie najściślejszy model regresji.
Dobroć dopasowania modelu regresji
Aby określić stopień dopasowania modelu regresji, zazwyczaj stosuje się współczynnik determinacji , który jest współczynnikiem statystycznym wskazującym procent wyjaśniony przez model regresji. Zatem im wyższy współczynnik determinacji modelu, tym lepiej będzie on dostosowany do próbki danych.
![]()
Należy jednak zaznaczyć, że im więcej zmiennych posiada model regresji, tym wyższy będzie jego współczynnik determinacji. Z tego powodu skorygowany współczynnik determinacji jest również często używany do pomiaru dobroci dopasowania modelu. Skorygowany współczynnik determinacji jest odmianą poprzedniego współczynnika, który wskazuje procent wyjaśniony przez model regresji, penalizujący każdą zmienną objaśniającą uwzględnioną w modelu.
![]()
Dlatego też preferuje się wykorzystanie skorygowanego współczynnika determinacji do porównania dwóch modeli z wieloma różnymi zmiennymi, gdyż uwzględnia on liczbę zmiennych wchodzących w skład modelu.
Na koniec należy zauważyć, że test Chi-kwadrat można również zastosować do pomiaru dobroci dopasowania modelu regresji, chociaż zwykle stosuje się wartości dwóch poprzednich współczynników.
Konkretny przykład dobrego dopasowania
Na koniec zobaczymy rozwiązanie w zakresie jakości dostosowania, aby zakończyć asymilację tej koncepcji statystycznej.
- Przy tej samej serii danych wykonywane są dwa różne modele regresji liniowej, których wyniki można zobaczyć w poniższej tabeli. Z jakiego modelu najlepiej skorzystać?
| Model regresji 1 | Model regresji 2 | |
|---|---|---|
| Współczynnik determinacji | 57% | 64% |
| Skorygowany współczynnik determinacji | 49% | 43% |
| Liczba zmiennych objaśniających | 3 | 7 |
W tym przypadku zakładamy, że oba modele spełniają poprzednie założenia modeli regresji liniowej i dlatego pozostaje nam jedynie przeanalizować dobroć dopasowania modeli.
Model regresji 2 ma wyższy współczynnik determinacji niż model regresji 1, dlatego a priori wydaje się być lepszym modelem regresji, ponieważ jest w stanie lepiej wyjaśnić próbkę danych.
Jednakże Model Regresji 2 ma w modelu 7 zmiennych niezależnych, podczas gdy Model Regresji 1 ma tylko 3. Zatem Model 2 będzie znacznie bardziej skomplikowany i trudniejszy do interpretacji niż pierwszy model.
Dodatkowo, jeśli spojrzymy na skorygowany współczynnik determinacji, który uwzględnia liczbę zmiennych w modelu, model regresji 1 ma wyższy skorygowany współczynnik determinacji niż model regresji 2.
Podsumowując, choć lepiej jest zastosować model regresji 1, gdyż jego skorygowany współczynnik determinacji jest wyższy niż modelu regresji 2. model regresji 2 ma wyższy nieskorygowany współczynnik determinacji, dzieje się tak dlatego, że w regresji uwzględniono znacznie więcej zmiennych model 1. model, który zwiększa wartość tego współczynnika, ale utrudnia interpretację modelu iz pewnością pogarsza przewidywanie nowej wartości.
Do porównania modeli o różnej liczbie zmiennych najlepiej zastosować skorygowany współczynnik determinacji, gdyż penalizuje on każdą zmienną dodaną do modelu. Jak widać na tym przykładzie, zgodnie z nieskorygowanym współczynnikiem determinacji, model regresji 2 jest lepszy, natomiast dzięki skorygowanemu współczynnikowi determinacji możemy wiedzieć, że model regresji 1 jest w rzeczywistości lepszy.