Regresja wielomianowa
W tym artykule wyjaśniono, czym jest regresja wielomianowa w statystyce i jak jest wykonywana. Dodatkowo będzie można zobaczyć przykład wykonania regresji wielomianowej.
Co to jest regresja wielomianowa?
Regresja wielomianowa lub regresja wielomianowa to model regresji, w którym związek między zmienną niezależną X a zmienną zależną Y jest modelowany za pomocą wielomianu.
Na przykład równanie modelu regresji wielomianowej kwadratowej ma postać y=β 0 +β 1 x+β 2 x 2 +ε.
Regresja wielomianowa jest przydatna do dopasowywania zbiorów danych, których wykresy są krzywymi wielomianowymi. Jeśli zatem wykres punktowy próbki danych ma kształt paraboli, lepszym rozwiązaniem będzie skonstruowanie modelu regresji kwadratowej niż modelu regresji liniowej. W ten sposób równanie modelu regresji będzie lepiej pasować do próbki danych.
Należy zauważyć, że regresja wielomianowa jest rodzajem regresji nieliniowej, podobnie jak regresja wykładnicza i regresja logarytmiczna.
Wzór regresji wielomianowej
Równanie modelu regresji wielomianowej to y=β 0 +β 1 x+β 2 x 2 +β 3 x 3 …+β m x m +ε.
![]()
Złoto:
-

jest zmienną zależną.
-

jest zmienną niezależną.
-

jest stałą równania regresji wielomianowej.
-

jest współczynnikiem regresji powiązanym ze zmienną

.
-

Jest to błąd lub reszta, czyli różnica między wartością obserwowaną a wartością oszacowaną przez model.
Jeśli więc mamy próbkę o łącznej wartości
![]()
obserwacji możemy zaproponować model regresji wielomianowej w postaci macierzowej:
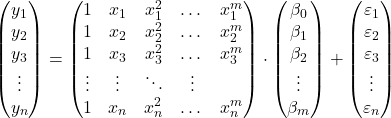
Powyższe wyrażenie macierzowe można przepisać, przypisując literę do każdej macierzy:
![]()
Zatem, stosując kryterium najmniejszych kwadratów , możemy otrzymać wzór na oszacowanie współczynników modelu regresji wielomianowej :
![]()
Ręczne wykonywanie tych obliczeń jest jednak bardzo pracochłonne i czasochłonne, dlatego wygodniej jest skorzystać z programów komputerowych (np. Minitab czy Excel), które pozwalają znacznie szybciej wykonać model regresji wielomianowej.
Przykład modelu regresji wielomianowej
Teraz, gdy znamy już definicję regresji wielomianowej i sposób jej przeprowadzania, spójrzmy na przykład z życia wzięty, aby w pełni zrozumieć tę koncepcję.
Przede wszystkim należy pamiętać, że model regresji wielomianowej należy wykonać, gdy wykres danych ma kształt krzywej wielomianowej. Na przykład, jeśli wykres punktowy ma postać krzywej sześciennej, musimy skonstruować model regresji wielomianowej trzeciego stopnia.
Zatem, jak widać na poniższym obrazku, wykres punktowy naszych danych ma kształt kwadratowy, ponieważ w miarę zwiększania wartości zmiennej niezależnej zmienna zależna rośnie szybciej. W tym przypadku wykonano model regresji liniowej i jak widać nie pasuje on dobrze do punktów, ponieważ posiada odcinki, w których linia znajduje się poniżej wszystkich punktów oraz odcinki, w których linia znajduje się nad nimi.
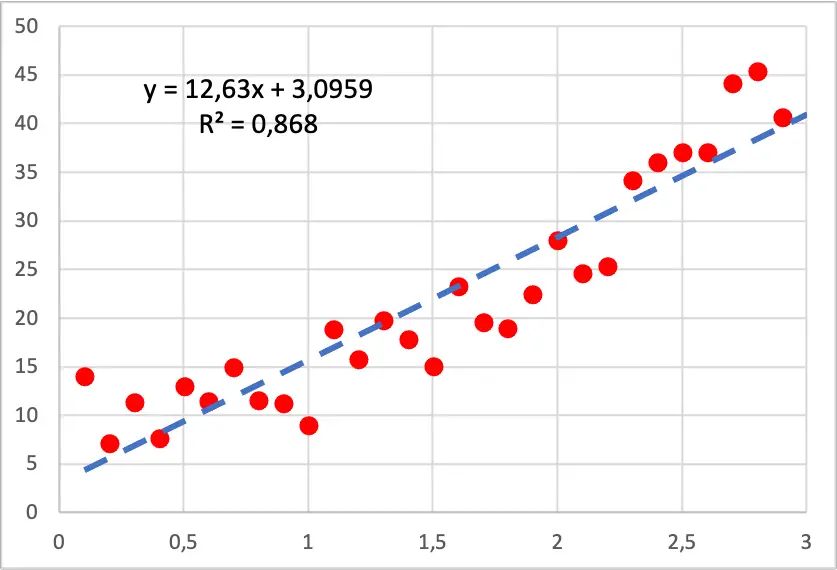
Z drugiej strony, jeśli uruchomimy model regresji wielomianowej kwadratowej, będzie on znacznie lepiej pasował do przykładowych danych, jak widać na poniższym obrazku.

Ponadto przy opracowywaniu modelu regresji wielomianowej współczynnik determinacji znacznie się poprawia, ponieważ wzrasta z 86,80% do 94,05%. Dlatego nowy model regresji znacznie lepiej wyjaśnia zbiór danych.
Z drugiej strony kolejną wskazówką, że musimy przeprowadzić regresję wielomianową, jest wykreślenie reszt. Jeśli w regresji liniowej wykres reszt ma kształt paraboli lub innego rodzaju wielomianu, model regresji wielomianowej z pewnością lepiej pasuje do badanych danych.
Inne rodzaje regresji nieliniowej
Istnieją głównie trzy typy regresji nieliniowej:
- Regresja wielomianowa – równanie modelu regresji ma postać wielomianu.
- Regresja logarytmiczna : przyjmuje się logarytm zmiennej niezależnej.
- Regresja wykładnicza : Zmienna niezależna znajduje się w wykładniku równania.