Heteroskedastyczność

W tym artykule wyjaśniono, czym jest heteroskedastyczność w statystyce. Dodatkowo dowiesz się co jest przyczyną heteroskedastyczności, jakie są jej konsekwencje i jak sobie z nią poradzić.

Co to jest heteroskedastyczność?

W statystyce heteroskedastyczność jest cechą przedstawiającą wzór regresji, który sugeruje, że wariancja błędu nie jest stała. Innymi słowy, model heteroskedastyczny oznacza, że jego błędy mają nieregularną wariancję, wówczas model nazywa się heteroskedastycznym.

Pamiętaj, że błąd (resztę) definiuje się jako różnicę między wartością rzeczywistą a wartością oszacowaną przez model regresji.

Podczas budowania modelu regresji błąd popełniany przez każdą obserwację jest obliczany przy użyciu poprzedniego wyrażenia. Zatem model statystyczny jest heteroskedastyczny, gdy wariancja obliczonych błędów nie jest stała w trakcie obserwacji, ale raczej się zmienia.

Choć może się to wydawać bardzo proste, ważne jest, aby model regresji nie przedstawiał heteroskedastyczności, gdyż obliczenia modelu opierają się na fakcie, że wariancja reszt jest stała, w istocie jest to jedno z poprzednich założeń modele regresji.

Istnieją pewne testy statystyczne, które mogą wykryć heteroskedastyczność, takie jak test White’a lub test Goldfelda-Quandta. Jednak zwykle poprzez wykreślenie reszt można zidentyfikować ich heteroskedastyczność.

Przyczyny heteroskedastyczności

Najczęstszymi przyczynami heteroskedastyczności w modelu są:

• Gdy zakres danych jest bardzo szeroki w porównaniu do średniej. Jeśli w tej samej próbie statystycznej występują wartości bardzo duże i bardzo małe, jest prawdopodobne, że uzyskany model regresji jest heteroskedastyczny.
• Pominięcie zmiennych w modelu regresji również skutkuje heteroskedastycznością. Logicznie rzecz biorąc, jeśli odpowiednia zmienna nie zostanie uwzględniona w modelu, jej zmienność zostanie uwzględniona w resztach i niekoniecznie zostanie ustalona.
• Podobnie zmiana struktury może spowodować słabe dopasowanie modelu do zbioru danych i dlatego wariancja reszt może nie być stała.
• Gdy niektóre zmienne mają znacznie większe wartości niż pozostałe zmienne objaśniające, model może wykazywać heteroskedastyczność. W takim przypadku zmienne można zrelatywizować, aby rozwiązać problem.

Jednak niektóre przypadki z natury mogą wykazywać heteroskedastyczność. Na przykład, jeśli modelujemy dochód danej osoby na podstawie jej wydatków na żywność, bogatsi ludzie charakteryzują się znacznie większą zmiennością w wydatkach na żywność niż ludzie biedniejsi. Ponieważ bogaty człowiek czasami jada w drogich restauracjach, a innym razem w tanich restauracjach, w przeciwieństwie do biednego człowieka, który zawsze jada w tanich restauracjach. Dlatego model regresji łatwo charakteryzuje się heteroskedastycznością.

Konsekwencje heteroskedastyczności

Głównie konsekwencje heteroskedastyczności w modelu regresji są następujące:

• W estymatorze metodą najmniejszych kwadratów, zdefiniowanym jako średnia kwadratów błędów, traci się wydajność.
• W obliczeniach macierzy kowariancji estymatorów metodą najmniejszych kwadratów występują błędy.

Prawidłowa heteroskedastyczność

Gdy powstały model regresji jest heteroskedastyczny, możemy wypróbować następujące poprawki, aby uzyskać heteroskedastyczność:

• Oblicz logarytm naturalny zmiennej niezależnej. Jest to ogólnie przydatne, gdy wariancja reszt na wykresie rośnie.
• W zależności od wykresu reszt, bardziej praktyczny może być inny rodzaj transformacji zmiennej niezależnej. Na przykład, jeśli wykres ma kształt paraboli, możemy obliczyć kwadrat zmiennej niezależnej i dodać tę zmienną do modelu.
• W modelu można również zastosować inne zmienne; usuwając lub dodając zmienną, można modyfikować wariancję reszt.
• Zamiast stosować kryterium najmniejszych kwadratów, można zastosować ważone kryterium najmniejszych kwadratów.

Heteroscedastyczność i homoskedastyczność

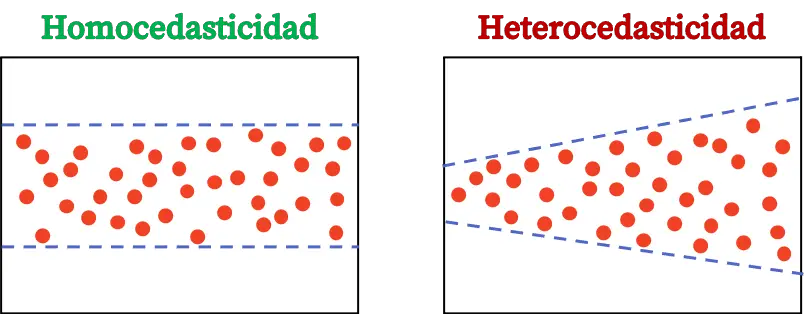
Na koniec zobaczymy, jakie są różnice między heteroskedastycznością a homoskedastycznością w statystyce, ponieważ są to dwie koncepcje modeli regresji, co do których musimy mieć jasność.

Homoscedastyczność modelu regresji jest cechą statystyczną wskazującą, że wariancja błędu jest stała. Zatem model homoskedastyczny oznacza, że wariancja jego błędów jest stała.

Różnicę między heteroskedastycznością a homoskedastycznością można znaleźć w stałości wariancji reszt. Jeśli wariancja reszt modelu nie jest stała, oznacza to, że model jest heteroskedastyczny. Z drugiej strony, jeśli wariancja reszt jest stała, oznacza to, że jest homoskedastyczna.

Dlatego musimy upewnić się, że budowany przez nas model regresji jest homoskedastyczny, w ten sposób spełnione zostanie założenie, że wariancja reszt jest stała.