Jak przetestować normalność w pythonie (4 metody)

Wiele testów statystycznych zakłada , że zbiory danych mają rozkład normalny.

Istnieją cztery typowe sposoby sprawdzania tej hipotezy w Pythonie:

1. (Metoda wizualna) Utwórz histogram.

• Jeżeli histogram ma w przybliżeniu kształt dzwonu, zakłada się, że dane mają rozkład normalny.

2. (Metoda wizualna) Utwórz wykres QQ.

• Jeżeli punkty na wykresie leżą w przybliżeniu na prostej ukośnej, wówczas zakłada się, że dane mają rozkład normalny.

3. (Formalny test statystyczny) Wykonaj test Shapiro-Wilka.

• Jeżeli wartość p testu jest większa niż α = 0,05, wówczas zakłada się, że dane mają rozkład normalny.

4. (Formalny test statystyczny) Wykonaj test Kołmogorowa-Smirnowa.

• Jeżeli wartość p testu jest większa niż α = 0,05, wówczas zakłada się, że dane mają rozkład normalny.

Poniższe przykłady pokazują, jak zastosować każdą z tych metod w praktyce.

Metoda 1: Utwórz histogram

Poniższy kod pokazuje, jak utworzyć histogram dla zbioru danych o rozkładzie logarytmiczno-normalnym :

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

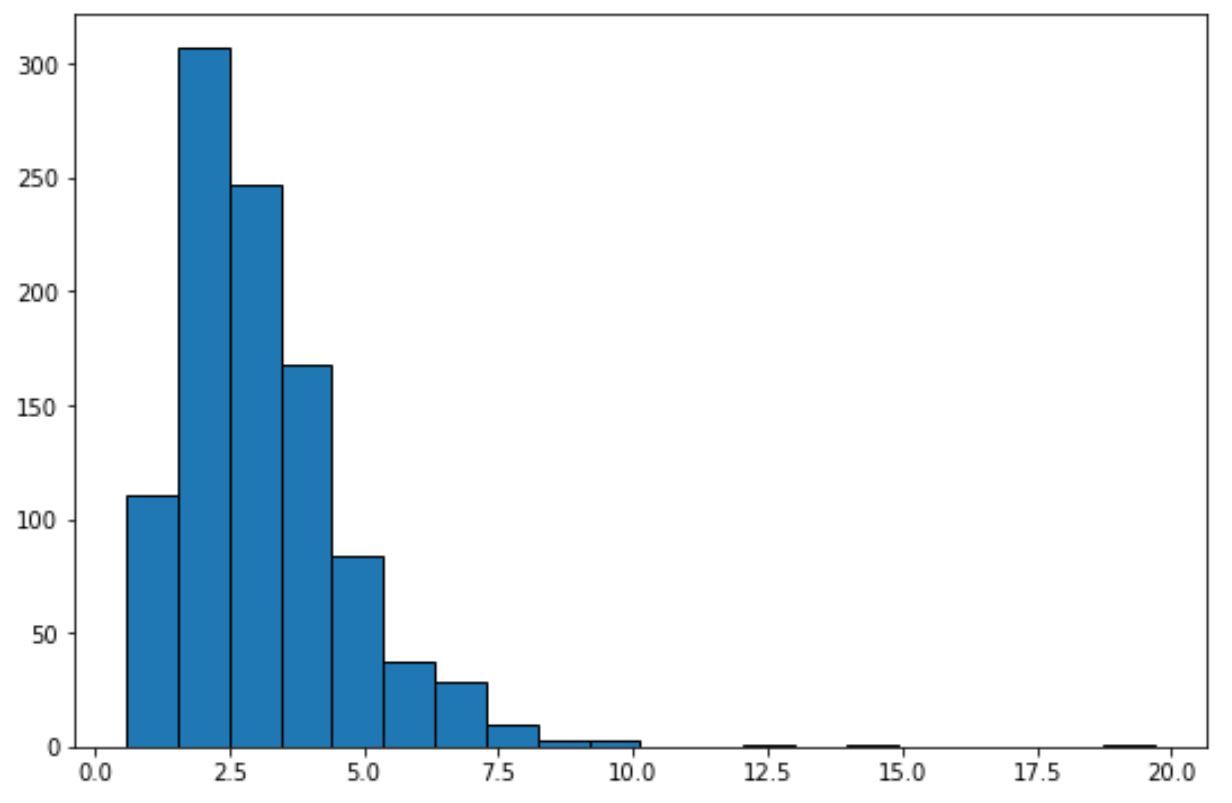
Patrząc na ten histogram, możemy stwierdzić, że zbiór danych nie ma „kształtu dzwonu” i nie ma rozkładu normalnego.

Metoda 2: Utwórz wykres QQ

Poniższy kod pokazuje, jak utworzyć wykres QQ dla zbioru danych o rozkładzie logarytmiczno-normalnym:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

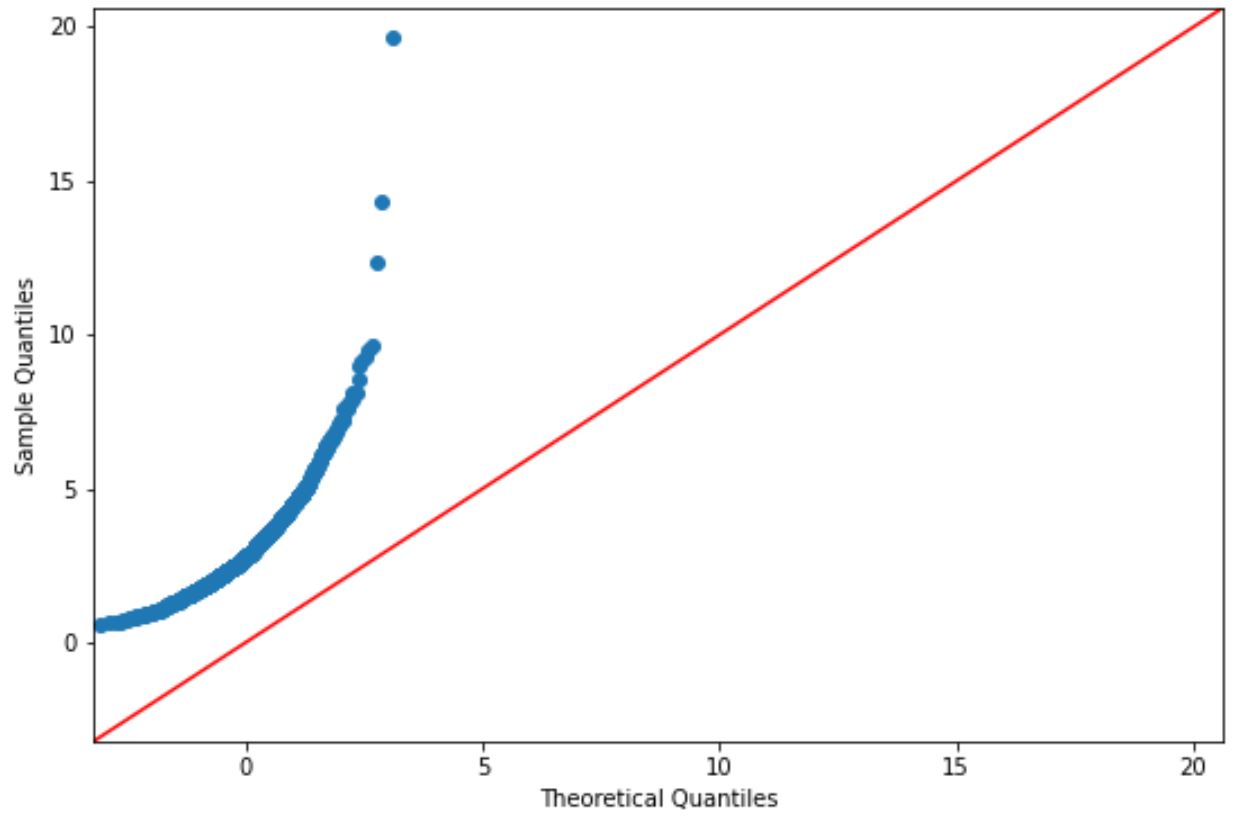
Jeśli punkty wykresu leżą w przybliżeniu na prostej ukośnej, ogólnie zakładamy, że zbiór danych ma rozkład normalny.

Jednak punkty na tym wykresie wyraźnie nie odpowiadają czerwonej linii, więc nie możemy założyć, że ten zbiór danych ma rozkład normalny.

Powinno to mieć sens, biorąc pod uwagę, że dane wygenerowaliśmy przy użyciu funkcji rozkładu logarytmiczno-normalnego.

Metoda 3: Wykonaj test Shapiro-Wilka

Poniższy kod pokazuje, jak wykonać Shapiro-Wilka dla zbioru danych o rozkładzie logarytmiczno-normalnym:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

Z wyniku widzimy, że statystyka testowa wynosi 0,857 , a odpowiadająca jej wartość p wynosi 3,88e-29 (skrajnie bliska zera).

Ponieważ wartość p jest mniejsza niż 0,05, odrzucamy hipotezę zerową testu Shapiro-Wilka.

Oznacza to, że mamy wystarczające dowody, aby stwierdzić, że przykładowe dane nie pochodzą z rozkładu normalnego.

Metoda 4: Wykonaj test Kołmogorowa-Smirnowa

Poniższy kod ilustruje sposób przeprowadzenia testu Kołmogorowa-Smirnowa dla zbioru danych o rozkładzie logarytmiczno-normalnym:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

Z wyniku widzimy, że statystyka testowa wynosi 0,841 , a odpowiadająca jej wartość p wynosi 0,0 .

Ponieważ wartość p jest mniejsza niż 0,05, odrzucamy hipotezę zerową testu Kołmogorowa-Smirnowa.

Oznacza to, że mamy wystarczające dowody, aby stwierdzić, że przykładowe dane nie pochodzą z rozkładu normalnego.

Jak postępować z nietypowymi danymi

Jeśli dany zbiór danych nie ma rozkładu normalnego, często możemy wykonać jedną z następujących transformacji, aby uzyskać bardziej normalny rozkład:

1. Transformacja logu: przekształć wartości x w log(x) .

2. Transformacja pierwiastka kwadratowego: Przekształć wartości x na √x .

3. Transformacja pierwiastka sześciennego: przekształć wartości x na x ^1/3 .

Wykonując te przekształcenia, zbiór danych ogólnie ma rozkład bardziej normalny.

Przeczytaj ten samouczek , aby zobaczyć, jak wykonać te transformacje w Pythonie.