Jak interpretować sygn. wartości (dwustronne) w spss
Często podczas wykonywania testów statystycznych w SPSS tabela wyjściowa zawiera znak Sig. wartość (dwustronna) .
Wartość ta reprezentuje dwustronną wartość p testu.
Jeśli ta wartość jest poniżej poziomu istotności (najczęściej wybierane wartości to 0,05 lub 0,01), możesz odrzucić hipotezę zerową swojego testu.
Ten samouczek zawiera przykłady interpretacji Sig. (dwustronna) wartość różnych testów statystycznych.
Przykład 1: Test t dla jednej próby
Test t dla jednej próby służy do sprawdzenia, czy średnia populacji jest równa określonej wartości.
Załóżmy na przykład, że botanik chce wiedzieć, czy średnia wysokość określonego gatunku rośliny wynosi 15 cali. Bierze losową próbkę 12 roślin i zapisuje wysokość każdej z nich w calach.
Następnie wykorzystuje tę próbkę do przeprowadzenia testu t dla jednej próby z następującymi hipotezami zerowymi i alternatywnymi:
- H 0 : μ = 15 (rzeczywista średnia populacji wynosi 15 cali)
- H A : μ ≠ 15 (rzeczywista średnia populacji nie jest równa 15 cali)
Przeprowadza ten test t dla jednej próby w SPSS i otrzymuje następujące wyniki:
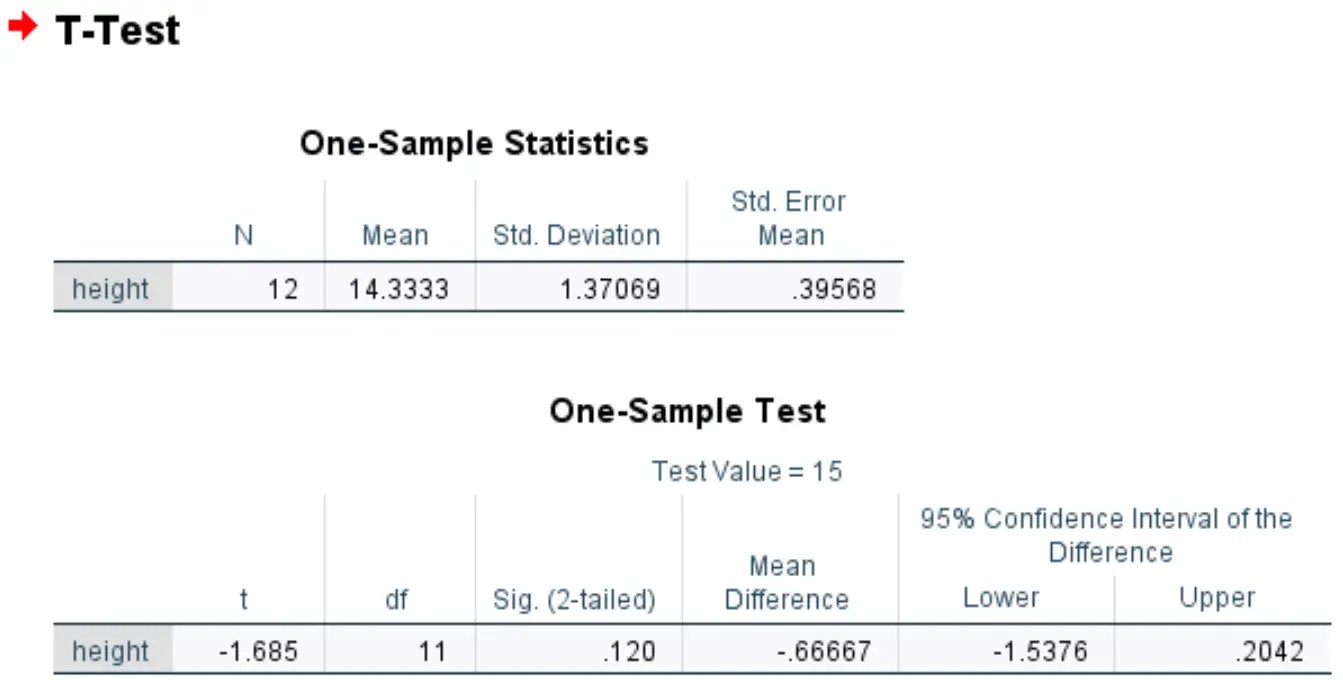
Syg. Wartość (dwustronna) wynosi 0,120 .
Stanowi to dwustronną wartość p, która odpowiada wartości -1,685 przy 11 stopniach swobody.
Ponieważ wartość p testu (0,120) jest nie mniejsza niż 0,05, nie udaje nam się odrzucić hipotezy zerowej.
Innymi słowy, nie mamy wystarczających dowodów, aby stwierdzić, że prawdziwa średnia wysokość tego gatunku roślin jest inna niż 15 cali.
Przykład 2: Test t dla dwóch próbek
Test t dla dwóch próbek służy do sprawdzenia, czy średnie wartości dwóch populacji są równe, czy nie.
Załóżmy na przykład, że badacze chcą wiedzieć, czy nowy sposób uzdatniania paliwa powoduje zmianę średniego przebiegu na galon danego samochodu. Aby to sprawdzić, przeprowadzają eksperyment, w którym 12 samochodów otrzymuje nowe uzdatnienie paliwa, a 12 samochodów nie.
Badacze przeprowadzają test t dla dwóch prób, przyjmując następujące hipotezy zerowe i alternatywne:
- H 0 : μ 1 = μ 2 (średnie mpg w obu populacjach jest równe)
- H 1 : μ 1 ≠ μ 2 (średnie mpg w obu populacjach nie jest równe)
Wykonują test t dla dwóch próbek w SPSS i uzyskują następujące wyniki:
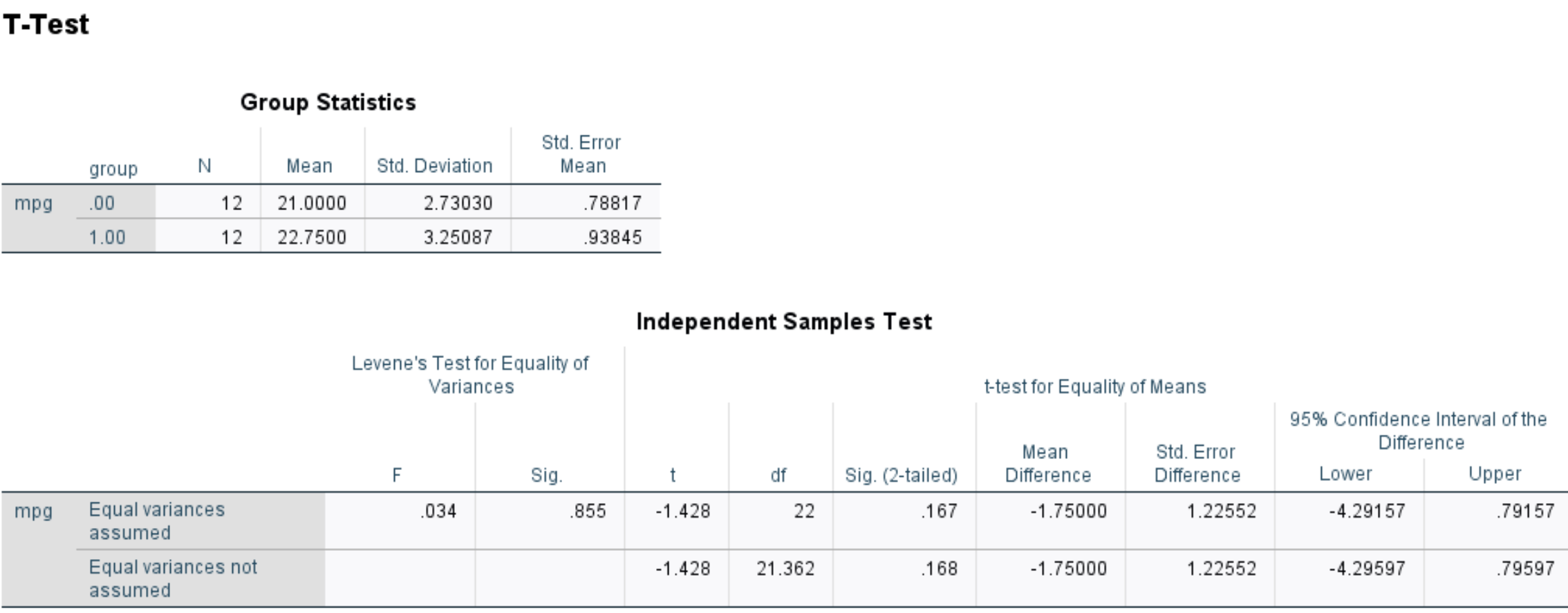
Syg. Wartość (dwustronna) wynosi 0,167 .
Stanowi to dwustronną wartość p, która odpowiada wartości -1,428 przy 22 stopniach swobody.
Ponieważ wartość p testu (0,167) jest nie mniejsza niż 0,05, nie udaje nam się odrzucić hipotezy zerowej.
Innymi słowy, nie mamy wystarczających dowodów, aby stwierdzić, że rzeczywista średnia wartość mpg różni się w przypadku samochodów poddanych leczeniu i tych, które tego nie robią.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak wykonywać różne testy statystyczne w SPSS:
Jak wykonać test t dla jednej próby w SPSS
Jak wykonać test t dla dwóch próbek w SPSS
Jak wykonać test t dla sparowanych próbek w SPSS