Związek między średnią a odchyleniem standardowym (z przykładem)
Średnia reprezentuje średnią wartość w zestawie danych.
Oblicza się go w następujący sposób:
Średnia próbki = Σx i / n
Złoto:
- Σ: Symbol oznaczający „sumę”
- x i : i -ta obserwacja w zbiorze danych
- n: całkowita liczba obserwacji w zbiorze danych
Odchylenie standardowe reprezentuje rozkład wartości w zbiorze danych w stosunku do średniej.
Oblicza się go w następujący sposób:
Odchylenie standardowe próbki = √ Σ(x i – x bar ) 2 / (n-1)
Złoto:
- Σ: Symbol oznaczający „sumę”
- x i : i-ta wartość próbki
- x słupek : Oznacza próbkę
- n: Wielkość próbki
Zwróć uwagę na związek między średnią a odchyleniem standardowym: we wzorze do obliczenia odchylenia standardowego używana jest średnia .
W rzeczywistości nie możemy obliczyć odchylenia standardowego próbki, jeśli nie znamy średniej próbki.
Poniższy przykład pokazuje, jak w praktyce obliczyć średnią próbki i odchylenie standardowe próbki dla zbioru danych.
Przykład: Obliczanie średniej i odchylenia standardowego dla zbioru danych
Załóżmy, że mamy następujący zbiór danych przedstawiający punkty zdobyte przez 10 różnych koszykarzy:
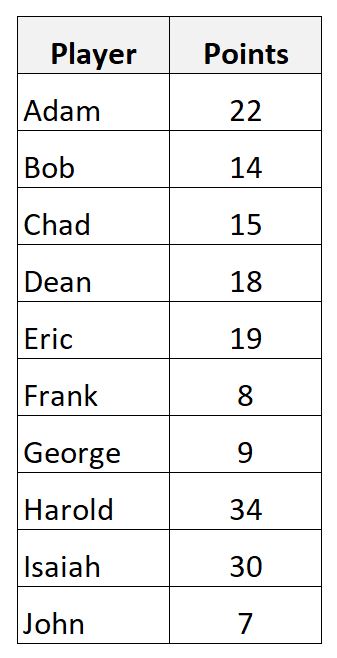Przykładową średnią zdobytych punktów możemy obliczyć korzystając ze wzoru:
- Średnia próbki = Σx i / n
- Średnia próbki = (22+14+15+18+19+8+9+34+30+7) / 10
- Średnia próbki = 17,6
Przykładowa średnia zdobytych punktów wynosi 17,6 . Oznacza średnią liczbę punktów zdobytych przez wszystkich graczy.
Kiedy już znamy średnią próbki, możemy ją podłączyć do wzoru, aby obliczyć odchylenie standardowe próbki:
- Odchylenie standardowe próbki = √ Σ(x i – x bar ) 2 / (n-1)
- Odchylenie standardowe próbki = √ ((22-17,6) 2 + (14-17,6) 2 + (15-17,6) 2 + (18-17,6) 2 + (19-17,6) 6) 2 + (8-17,6) 2 + (9 -17,6) 2 + (34-17,6) 2 + (30-17,6) 2 + (7-17,6) 2 ) / (10-1)
- Próbka odchylenie standardowe = 9,08
Odchylenie standardowe próbki wynosi 9,08 . Reprezentuje średnią odległość między wartością każdego punktu a średnią punktu próbki.
Warto znać zarówno średnią, jak i odchylenie standardowe zbioru danych, ponieważ każda metryka mówi nam coś innego.
Średnia daje nam wyobrażenie o tym, gdzie leży „centralna” wartość zbioru danych.
Odchylenie standardowe daje nam wyobrażenie o rozkładzie wartości wokół średniej w zbiorze danych. Im wyższa wartość odchylenia standardowego, tym bardziej rozproszone są wartości w próbce.
Znając te dwie wartości, możemy wiele dowiedzieć się o rozkładzie wartości w zbiorze danych.
Dodatkowe zasoby
Poniższe samouczki zawierają dodatkowe informacje na temat średniej i odchylenia standardowego:
Dlaczego średnia jest ważna w statystyce?
Dlaczego odchylenie standardowe jest ważne w statystyce?
Jak obliczyć średnią i odchylenie standardowe w programie Excel
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej