Jak używać metody elbow w r, aby znaleźć optymalne klastry

Jednym z najczęściej używanych algorytmów grupowania w uczeniu maszynowym jest grupowanie k-średnich .

Grupowanie K-średnich to technika, w której każdą obserwację ze zbioru danych umieszczamy w jednym z K klastrów.

Ostatecznym celem jest utworzenie K klastrów, w których obserwacje w każdym klastrze są do siebie dość podobne, podczas gdy obserwacje w różnych klastrach znacznie się od siebie różnią.

Wykonując grupowanie k-średnich, pierwszym krokiem jest wybranie wartości K – liczby skupień, w których chcemy umieścić obserwacje.

Jednym z najczęstszych sposobów wyboru wartości K jest metoda łokcia , która polega na utworzeniu wykresu zawierającego liczbę skupień na osi x i sumę kwadratów na osi y, a następnie zidentyfikowanie gdzie na działce pojawia się „kolano” lub zakręt.

Punkt na osi x, w którym występuje „kolano”, mówi nam o optymalnej liczbie skupień do wykorzystania w algorytmie grupowania k-średnich.

Poniższy przykład pokazuje, jak używać metody łokcia w R.

Przykład: użycie metody łokcia w R

W tym przykładzie użyjemy zbioru danych USArrests wbudowanego w R, który zawiera liczbę aresztowań na 100 000 mieszkańców w każdym stanie USA w 1973 r. za morderstwo, napaść i gwałt, a także odsetek populacji każdego stanu mieszkającej w obszarach miejskich obszary. , UrbanPop.

Poniższy kod pokazuje, jak załadować zbiór danych, usunąć wiersze z brakującymi wartościami i przeskalować każdą zmienną w zbiorze danych, aby uzyskać średnią wynoszącą 0 i odchylenie standardowe wynoszące 1:

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Aby znaleźć optymalną liczbę skupień do wykorzystania w algorytmie k-średnich, użyjemy funkcji fviz_nbclust() z pakietu factoextra , aby utworzyć wykres liczby skupień względem sumy kwadratów:

 library (cluster)
library (factoextra)

#create plot of number of clusters vs total within sum of squares
fviz_nbclust(df, kmeans, method = “ wss ”) 

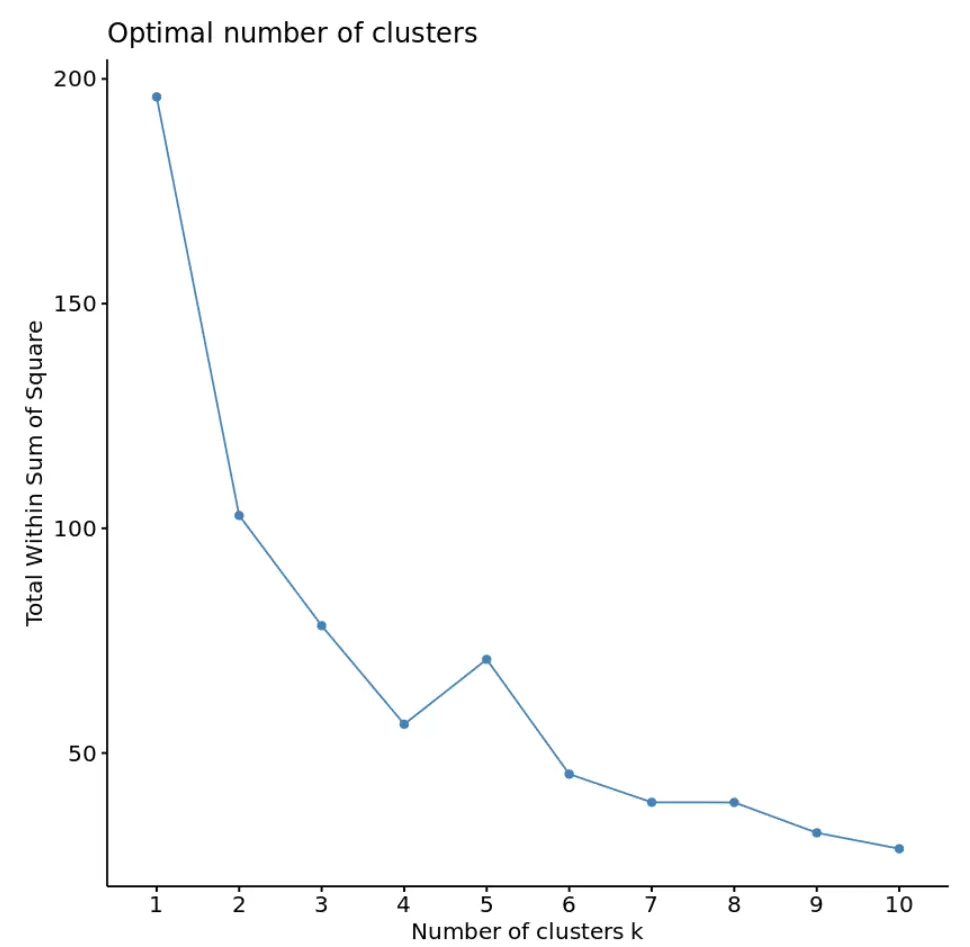
Na tym wykresie wydaje się, że w k = 4 skupiskach występuje „kolano” lub załamanie. Jest to punkt, w którym suma kwadratów zaczyna się stabilizować.

Mówi nam to, że optymalna liczba klastrów do wykorzystania w algorytmie k-średnich wynosi 4.

Uwaga : chociaż przy użyciu większej liczby klastrów moglibyśmy uzyskać niższą sumę kwadratów, prawdopodobnie doszłoby do nadmiernego dopasowania danych uczących i dlatego algorytm k-średnich nie działałby tak dobrze na danych testowych.

Możemy użyć funkcji kmeans() z pakietu klastra , aby wykonać grupowanie k-średnich na zbiorze danych przy użyciu optymalnej wartości k z 4:

 #make this example reproducible
set. seeds (1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

Z wyników możemy zobaczyć, że:

• Do pierwszego skupienia przypisano 16 stanów
• Do drugiego skupienia przypisano 13 stanów
• Do trzeciego skupienia przypisano 13 stanów
• Do czwartego skupienia przypisano 8 stanów

Możemy również dodać przypisania klastrów każdego stanu do oryginalnego zbioru danych:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Każdą obserwację z oryginalnej bazy danych umieszczono w jednej z czterech grup.

Dodatkowe zasoby

Poniższe samouczki zawierają szczegółowe przykłady uruchamiania różnych algorytmów grupowania w języku R:

Grupowanie K-średnich w R: Przykład krok po kroku
Klastrowanie K-Medoids w R: przykład krok po kroku
Klastrowanie hierarchiczne w R: przykład krok po kroku