Reguła dodawania (lub reguła dodawania)

W tym artykule wyjaśniono, czym jest zasada dodawania, zwana także zasadą dodawania, i do czego służy w prawdopodobieństwie i statystyce. Dodatkowo będziesz mógł zobaczyć jaki jest wzór na regułę dodawania oraz rozwiązane ćwiczenia pokazujące jak z niego skorzystać.

Jaka jest zasada dodawania (lub zasada dodawania)?

Reguła dodawania (lub zasada dodawania ) stwierdza, że suma prawdopodobieństw dwóch zdarzeń jest równa sumie prawdopodobieństwa wystąpienia każdego zdarzenia osobno pomniejszonej o prawdopodobieństwo wystąpienia obu zdarzeń w tym samym czasie.

Zatem wzór na regułę dodawania to P(A⋃B)=P(A)+P(B)−P(A⋂B).

Zatem, aby dodać dwa prawdopodobieństwa, nie możemy po prostu dodać każdego prawdopodobieństwa, ponieważ musimy również odjąć wyraz reprezentujący łączne prawdopodobieństwo dwóch zdarzeń. Jednak w niektórych przypadkach dopiero dodając prawdopodobieństwo każdego zdarzenia możemy otrzymać prawidłowy wynik sumy prawdopodobieństw. Poniżej zobaczymy, jakie to są przypadki.

Krótko mówiąc, reguła dodawania służy do obliczenia prawdopodobieństwa wystąpienia tego lub innego zdarzenia, to znaczy prawdopodobieństwa wystąpienia co najmniej jednego z dwóch możliwych zdarzeń.

Formuła reguły dodawania

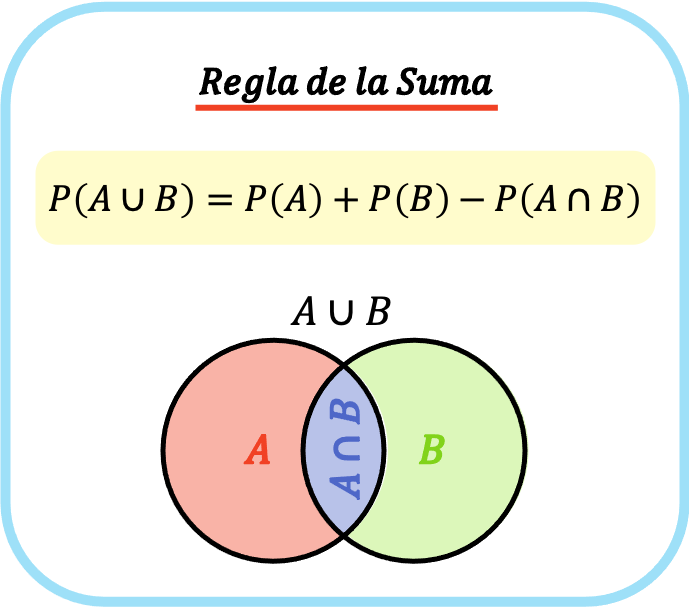
Zasada dodawania mówi, że aby obliczyć prawdopodobieństwo wystąpienia zdarzenia A lub zdarzenia B, należy dodać prawdopodobieństwo wystąpienia zdarzenia A i prawdopodobieństwo wystąpienia zdarzenia B i odjąć prawdopodobieństwo, że oba zdarzenia wystąpią w tym samym czasie. .

Wzór na regułę dodawania (lub regułę dodawania) jest zatem następujący:

Złoto:

• 

  jest prawdopodobieństwem zdarzenia A lub zdarzenia B.

• 

  jest prawdopodobieństwem wystąpienia zdarzenia A.

• 

  jest prawdopodobieństwem wystąpienia zdarzenia B.

• 

  jest łącznym prawdopodobieństwem wystąpienia zdarzenia A i zdarzenia B.

Dlatego, aby skorzystać z reguły sumy, musisz wiedzieć, jak obliczyć łączne prawdopodobieństwo dwóch zdarzeń. Jak to się robi, możesz zobaczyć pod poniższym linkiem:

Przykładowa reguła sumy dla ekskluzywnych wydarzeń

Aby zakończyć zrozumienie tej koncepcji, zobaczmy przykład zastosowania reguły dodawania.

• Do pudełka wkładamy 10 kul niebieskich, 6 kulek pomarańczowych i 4 kulki zielone. Jakie jest prawdopodobieństwo, że wylosujemy kulę niebieską lub pomarańczową?

Ćwiczenie wymaga od nas określenia prawdopodobieństwa wystąpienia tego lub innego zdarzenia. Dlatego, aby rozwiązać problem, musimy skorzystać ze wzoru na regułę dodawania:

Zatem najpierw obliczamy prawdopodobieństwo wystąpienia każdego zdarzenia osobno, korzystając z reguły Laplace’a :

Jednak w tym przypadku oba zdarzenia nie mogą wystąpić w tym samym czasie, ponieważ są to dwa zdarzenia wzajemnie się wykluczające . Zatem jeśli wylosujemy niebieską kulę, nie będziemy już mogli wylosować pomarańczowej kuli i odwrotnie.

Zatem łączne prawdopodobieństwo obu zdarzeń wynosi zero, stąd wzór na regułę sumy jest uproszczony:

Zatem obliczenie prawdopodobieństwa złapania piłki niebieskiej lub pomarańczowej jest następujące:

Krótko mówiąc, prawdopodobieństwo wylosowania niebieskiej lub pomarańczowej kuli z pudełka wynosi 80%.

Przykładowa reguła dołączania dla wydarzeń niewyłącznych

Po zapoznaniu się z konkretnym przykładem reguły dodawania, gdy zdarzenia mają charakter wykluczający, zobaczymy teraz, jak to prawo jest stosowane, gdy zdarzenia nie mają charakteru wyłącznego.

• Jeśli rzucimy monetą dwa razy, jakie jest prawdopodobieństwo, że w co najmniej jednym rzucie wypadnie reszka?

W tym przypadku zdarzenia nie wykluczają się wzajemnie, gdyż przy pierwszym rzucie możemy otrzymać „reszkę”, a przy drugim rzucie „reszkę”. Wzór na regułę dodawania nie jest zatem uproszczony i wygląda następująco:

Zatem najpierw musimy obliczyć prawdopodobieństwo wyrzucenia reszki w rzucie monetą, stosując regułę Laplace’a:

Dodatkowo oba zdarzenia są niezależne, więc możemy obliczyć łączne prawdopodobieństwo tych dwóch zdarzeń, korzystając z reguły iloczynu :

Na koniec, aby znaleźć prawdopodobieństwo, że orzeł spadnie w co najmniej jednym z dwóch rzutów, wystarczy podstawić wartości do wzoru reguły dodawania i wykonać obliczenia:

Podsumowując, prawdopodobieństwo, że przy dwukrotnym rzucie monetą przynajmniej raz wypadnie reszka, wynosi 75%.