Jak ustalić, czy rozkład prawdopodobieństwa jest prawidłowy

Rozkład prawdopodobieństwa mówi nam, jakie jest prawdopodobieństwo, że zmienna losowa przyjmie określone wartości.

Aby rozkład prawdopodobieństwa był ważny, musi spełniać dwa warunki:

1. Każde prawdopodobieństwo musi mieścić się w przedziale od 0 do 1.

2. Suma prawdopodobieństw musi wynosić 1.

Jeżeli te dwa warunki są spełnione, wówczas rozkład prawdopodobieństwa jest ważny.

Poniższe przykłady pokazują, jak sprawdzić, czy różne rozkłady prawdopodobieństwa są prawidłowe.

Przykład 1: Bramki zdobyte w meczu piłki nożnej

Poniższy rozkład prawdopodobieństwa pokazuje prawdopodobieństwo, że dana drużyna piłkarska zdobędzie określoną liczbę bramek w meczu:

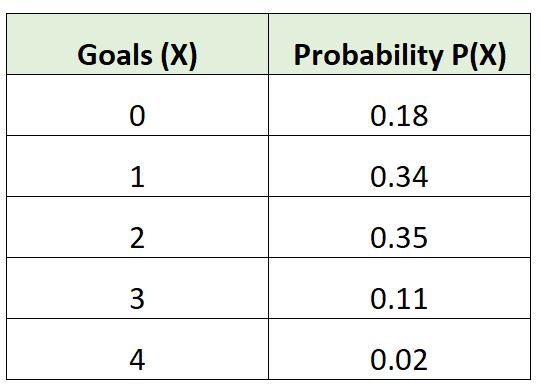
Sprawdźmy, czy ten rozkład prawdopodobieństwa spełnia oba warunki, aby był ważny:

1. Każde prawdopodobieństwo musi mieścić się w przedziale od 0 do 1.

Widzimy, że każde indywidualne prawdopodobieństwo mieści się w przedziale od 0 do 1.

2. Suma prawdopodobieństw musi wynosić 1.

Widzimy, że suma prawdopodobieństw wynosi 1:

Suma = 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1

Obydwa warunki są spełnione, więc ten rozkład prawdopodobieństwa jest prawidłowy .

Przykład 2: sprzedaż zrealizowana w ciągu jednego miesiąca

Poniższy rozkład prawdopodobieństwa pokazuje prawdopodobieństwo, że dany sprzedawca dokona w nadchodzącym miesiącu określonej liczby sprzedaży:

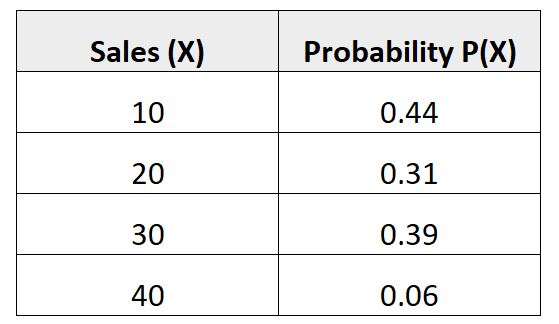
Sprawdźmy, czy ten rozkład prawdopodobieństwa spełnia oba warunki, aby był ważny:

1. Każde prawdopodobieństwo musi mieścić się w przedziale od 0 do 1.

Widzimy, że każde indywidualne prawdopodobieństwo mieści się w przedziale od 0 do 1.

2. Suma prawdopodobieństw musi wynosić 1.

Widzimy, że suma prawdopodobieństw nie sumuje się do 1:

Suma = 0,44 + 0,31 + 0,39 + 0,06 = 1,2

Oba warunki nie są spełnione i dlatego ten rozkład prawdopodobieństwa jest nieprawidłowy .

Przykład 3: Liczba awarii baterii

Poniższy rozkład prawdopodobieństwa informuje nas o prawdopodobieństwie, że w danym pojeździe wystąpi określona liczba awarii akumulatora w okresie 10 lat:

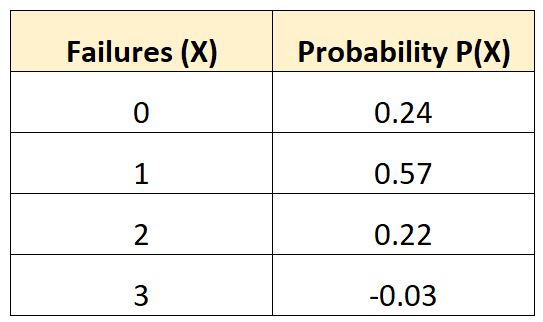
Sprawdźmy, czy ten rozkład prawdopodobieństwa spełnia oba warunki, aby był ważny:

1. Każde prawdopodobieństwo musi mieścić się w przedziale od 0 do 1.

Widzimy, że każde indywidualne prawdopodobieństwo nie mieści się w przedziale od 0 do 1.

Ostatnie prawdopodobieństwo w tabeli ma wartość ujemną.

2. Suma prawdopodobieństw musi wynosić 1.

Widzimy, że suma prawdopodobieństw wynosi 1:

Suma = 0,24 + 0,57 + 0,22 – 0,03 = 1

Oba warunki nie są spełnione i dlatego ten rozkład prawdopodobieństwa jest nieprawidłowy .

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat rozkładów prawdopodobieństwa:

Jak znaleźć średnią rozkładu prawdopodobieństwa
Jak znaleźć wariancję rozkładu prawdopodobieństwa
Jak znaleźć odchylenie standardowe rozkładu prawdopodobieństwa