Co to jest rozkład próbkowania?

Wyobraź sobie, że populacja delfinów liczy 10 000, a średnia waga delfina w tej populacji wynosi 300 funtów.

Jeśli weźmiemy prostą losową próbkę 50 delfinów z tej populacji, możemy odkryć, że średnia waga delfinów w tej próbie wynosi 305 funtów.

Następnie, jeśli weźmiemy kolejną prostą losową próbkę 50 delfinów, możemy odkryć, że średnia waga delfinów w tej próbie wynosi 295 funtów.

Ilekroć bierzemy prostą losową próbkę 50 delfinów, jest prawdopodobne, że średnia waga delfinów w próbie jest zbliżona do średniej populacji wynoszącej 300 funtów, ale nie dokładnie 300 funtów.

Wyobraźmy sobie, że bierzemy 200 prostych losowych próbek 50 delfinów z tej populacji i tworzymy histogram średniej masy każdej próbki:

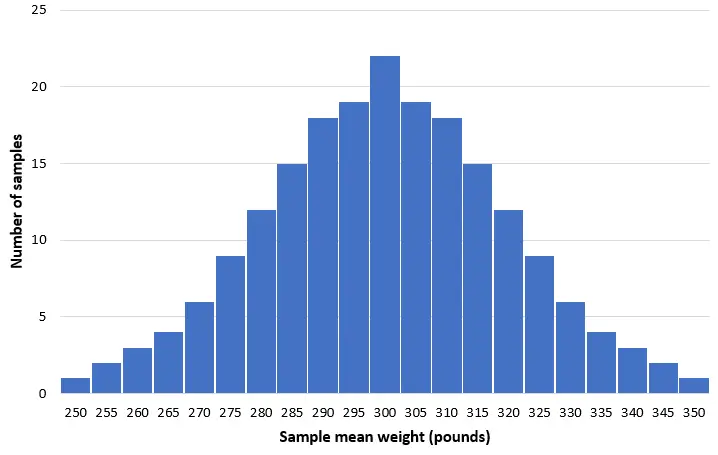
W większości próbek średnia waga będzie bliska 300 funtów. W rzadkich przypadkach możemy pobrać próbkę pełną małych delfinów, których średnia waga wynosi zaledwie 250 funtów. Możemy też pobrać próbkę pełną delfinów butlonosech, ważących średnio 350 funtów. Ogólnie rzecz biorąc, rozkład średnich z próby będzie w przybliżeniu normalny, ze środkiem rozkładu zlokalizowanym w prawdziwym środku populacji.

Ten rozkład średnich z próby nazywany jest rozkładem średniej z próbkowania i ma następujące właściwości:

_µx = µ

gdzie μ _x to średnia próbki, a μ to średnia populacji.

_σx = σ/√n

gdzie σ _x to odchylenie standardowe próby, σ to odchylenie standardowe populacji, a n to wielkość próby.

Na przykład w tej populacji delfinów wiemy, że średnia waga wynosi μ = 300. Zatem średnia rozkładu próbek wynosi μ _x = 300 .

Załóżmy, że wiemy również, że odchylenie standardowe populacji wynosi 18 funtów. Odchylenie standardowe próbki wynosi zatem σ _x = 18/ √50 = 2,546 .

Próbkowanie rozkładu proporcji

Rozważmy tę samą populację 10 000 delfinów. Załóżmy, że 10% delfinów jest czarnych, a reszta jest szara. Załóżmy, że bierzemy prostą losową próbkę 50 delfinów i stwierdzamy, że 14% delfinów w tej próbie jest czarnych. Następnie bierzemy kolejną prostą losową próbkę 50 delfinów i stwierdzamy, że 8% delfinów w tej próbie jest czarnych.

Wyobraź sobie, że bierzemy 200 prostych losowych próbek 50 delfinów z tej populacji i tworzymy histogram proporcji czarnych delfinów w każdej próbce:

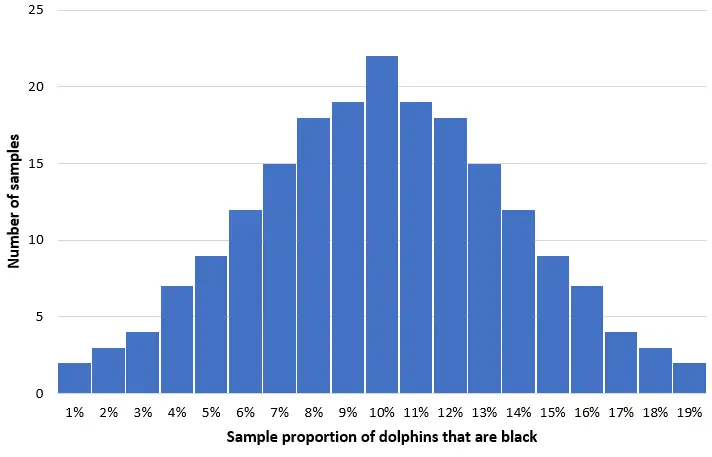
W większości próbek odsetek delfinów czarnych będzie zbliżony do rzeczywistej populacji wynoszącej 10%. Rozkład proporcji próbki delfinów czarnych będzie w przybliżeniu normalny, ze środkiem rozkładu zlokalizowanym w prawdziwym środku populacji.

Ten rozkład proporcji próbki jest znany jako rozkład proporcji próbkowania i ma następujące właściwości:

_µp = P

gdzie p to odsetek próby, a P to odsetek populacji.

σ _p = √ (P)(1-P) / n

gdzie P to odsetek populacji, a n to wielkość próby.

Na przykład w tej populacji delfinów wiemy, że prawdziwy odsetek delfinów czarnych wynosi 10% = 0,1. Zatem średnia proporcjonalnego rozkładu próbkowania wynosi μ _p = 0,1 .

Załóżmy, że wiemy również, że odchylenie standardowe populacji wynosi 18 funtów. Zatem odchylenie standardowe próbki wynosi σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

Ustanów normalność

Aby skorzystać z powyższych wzorów, rozkład próbkowania musi być normalny.

Zgodnie z centralnym twierdzeniem granicznym rozkład średniej próbki jest w przybliżeniu normalny, jeśli wielkość próby jest wystarczająco duża, nawet jeśli rozkład populacji nie jest normalny . W większości przypadków za wystarczająco dużą uznajemy próbkę liczącą 30 lub więcej osób.

Rozkład próbkowania części próbki jest w przybliżeniu normalny, jeśli oczekiwana liczba sukcesów i niepowodzeń wynosi co najmniej 10.

Przykłady

Do obliczenia prawdopodobieństwa możemy użyć rozkładów próbkowania.

Przykład 1: Określona maszyna tworzy pliki cookie. Rozkład masy tych ciasteczek jest przesunięty w prawo, średnio 10 uncji i odchylenie standardowe 2 uncje. Jeśli weźmiemy prostą losową próbkę 100 ciasteczek wyprodukowanych przez to urządzenie, jakie jest prawdopodobieństwo, że średnia waga ciasteczek w tej próbce jest mniejsza niż 9,8 uncji?

Krok 1: Ustanów normalność.

Musimy upewnić się, że rozkład próbkowania średnich z próbki jest normalny. Ponieważ wielkość naszej próby jest większa lub równa 30, zgodnie z centralnym twierdzeniem granicznym, możemy założyć, że rozkład próbkowania średnich z próby jest normalny.

Krok 2: Znajdź średnią i odchylenie standardowe rozkładu próbkowania.

_µx = µ

_σx = σ/√n

μ _x = 10 uncji

σ _x = 2/ √100 = 2/10 = 0,2 uncji

Krok 3: Użyj kalkulatora powierzchni Z-Score , aby określić prawdopodobieństwo, że średnia waga ciasteczka w tej próbce jest mniejsza niż 9,8 uncji.

Wprowadź następujące liczby do kalkulatora obszaru wyniku Z. Możesz pozostawić pole „Raw Score 2” puste, ponieważ w tym przykładzie znajdujemy tylko jedną liczbę.

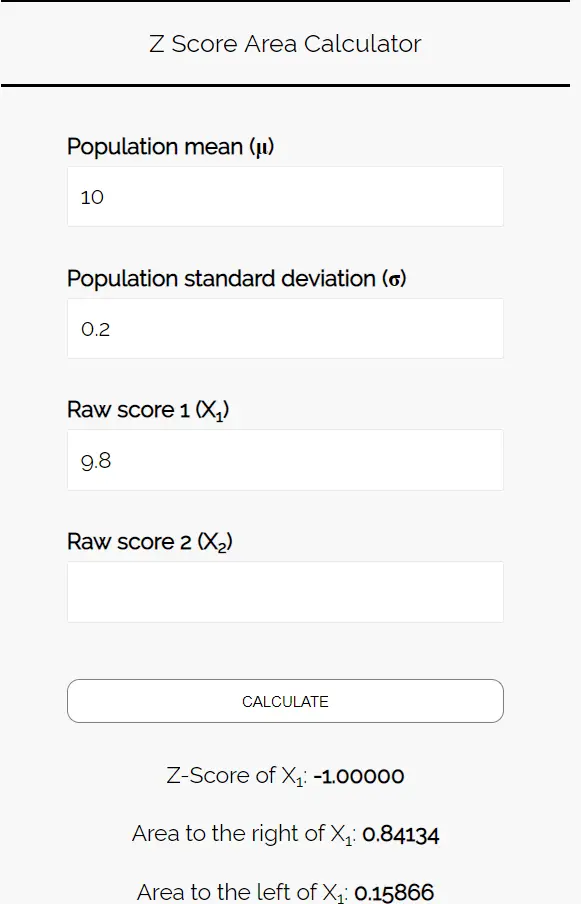
Ponieważ chcemy poznać prawdopodobieństwo, że średnia waga ciasteczek w tej próbce jest mniejsza niż 9,8 uncji, interesuje nas obszar na lewo od 9,8. Kalkulator mówi nam, że prawdopodobieństwo to wynosi 0,15866 .

Przykład 2: Według badania przeprowadzonego w całej szkole 87% uczniów w danej szkole woli pizzę od lodów. Załóżmy, że wybieramy prostą losową próbę 200 uczniów. Jakie jest prawdopodobieństwo, że odsetek uczniów preferujących pizzę będzie mniejszy niż 85%?

Krok 1: Ustanów normalność.

Przypomnijmy, że rozkład próbkowania części próbki jest w przybliżeniu normalny, jeśli oczekiwana liczba „sukcesów” i „porażek” wynosi co najmniej 10.

W tym przypadku oczekiwana liczba uczniów, którzy będą preferować pizzę, to 87% * 200 uczniów = 174 uczniów. Przewidywana liczba uczniów, którzy nie będą preferować pizzy to 13% * 200 uczniów = 26 uczniów. Ponieważ obie te liczby wynoszą co najmniej 10, możemy założyć, że rozkład próby odsetka uczniów, którzy wolą pizzę, jest w przybliżeniu normalny.

Krok 2: Znajdź średnią i odchylenie standardowe rozkładu próbkowania.

_µp = P

σ _p = √ (P)(1-P) / n

_µp = 0,87

σ _p = √ (0,87)(1-0,87) / 200 = 0,024

Krok 3: Skorzystaj z kalkulatora powierzchni Z-Score , aby określić prawdopodobieństwo, że odsetek uczniów preferujących pizzę będzie mniejszy niż 85%.

Wprowadź następujące liczby do kalkulatora obszaru wyniku Z. Możesz pozostawić pole „Raw Score 2” puste, ponieważ w tym przykładzie znajdujemy tylko jedną liczbę.

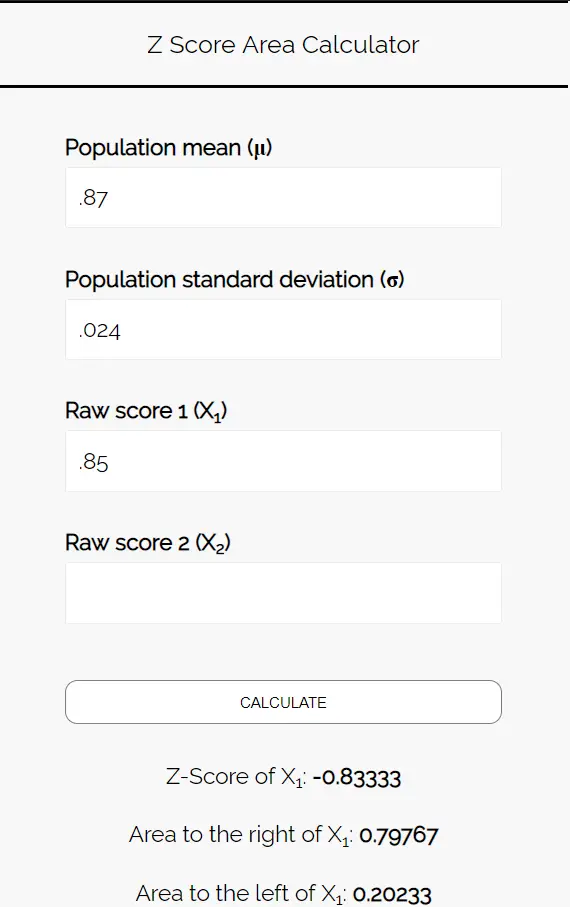
Ponieważ chcemy poznać prawdopodobieństwo, że odsetek uczniów preferujących pizzę będzie mniejszy niż 85%, interesuje nas obszar na lewo od 0,85. Kalkulator mówi nam, że prawdopodobieństwo to wynosi 0,20233 .