Jak sprawdzić znaczenie nachylenia regresji

Załóżmy, że mamy następujący zestaw danych, który pokazuje powierzchnię i cenę 12 różnych domów:

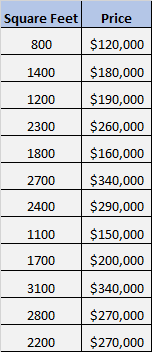
Chcemy wiedzieć, czy istnieje istotna zależność pomiędzy powierzchnią powierzchni a ceną.

Aby zorientować się, jak wyglądają dane, najpierw tworzymy wykres rozrzutu ze stopami kwadratowymi na osi x i ceną na osi y:

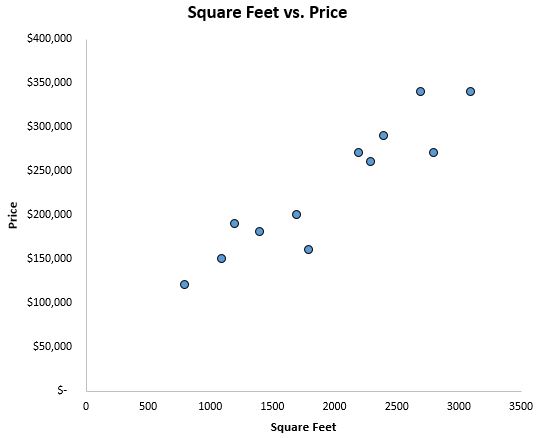
Wyraźnie widać, że istnieje pozytywna korelacja pomiędzy powierzchnią a ceną. Wraz ze wzrostem powierzchni użytkowej rośnie także cena domu.

Aby jednak dowiedzieć się, czy istnieje statystycznie istotna zależność pomiędzy powierzchnią a ceną, musimy przeprowadzić prostą regresję liniową.

Przeprowadzamy więc prostą regresję liniową , używając stóp kwadratowych jako predyktora i ceny jako odpowiedzi, i otrzymujemy następujący wynik:

Niezależnie od tego, czy przeprowadzisz prostą regresję liniową w Excelu, SPSS, R, czy innym oprogramowaniu, otrzymasz wynik podobny do pokazanego powyżej.

Pamiętaj, że prosta regresja liniowa da linię najlepszego dopasowania, czyli równanie linii, która najlepiej „pasuje” do danych na naszym wykresie rozrzutu. Ta linia najlepszego dopasowania jest zdefiniowana jako:

ŷ = b ₀ + b ₁ x

gdzie ŷ to przewidywana wartość zmiennej odpowiedzi, b ₀ to wyraz wolny, b ₁ to współczynnik regresji, a x to wartość zmiennej predykcyjnej.

Wartość b ₀ jest podana przez współczynnik pochodzenia, który wynosi 47588,70.

Wartość b ₁ jest określona przez współczynnik zmiennej predykcyjnej Square Feet , który wynosi 93,57.

Zatem najlepiej dopasowana linia w tym przykładzie to ŷ = 47588,70+ 93,57x

Oto jak interpretować tę linię najlepszego dopasowania:

• b ₀ : Gdy wartość stóp kwadratowych wynosi zero, oczekiwana średnia wartość ceny wynosi 47 588,70 USD. (W tym przypadku interpretacja wyrazu wolnego nie ma sensu, ponieważ dom nigdy nie może mieć zerowych stóp kwadratowych)
• b ₁ : Na każdy dodatkowy metr kwadratowy średni oczekiwany wzrost ceny wynosi 93,57 USD.

Wiemy już, że na każdy dodatkowy metr kwadratowy średni oczekiwany wzrost ceny wynosi 93,57 USD.

Aby wiedzieć, czy ten wzrost jest istotny statystycznie, musimy przeprowadzić test hipotezy dla B ₁ lub skonstruować przedział ufności dla B ₁ .

Uwaga : Test hipotezy i przedział ufności zawsze dają takie same wyniki.

Konstrukcja przedziału ufności dla nachylenia regresji

Aby skonstruować przedział ufności dla nachylenia regresji, używamy następującego wzoru:

Przedział ufności = b ₁ +/- (t _{1-∝/2, n-2} ) * (błąd standardowy b ₁ )

Złoto:

• b ₁ jest współczynnikiem nachylenia podanym w wyniku regresji
• (t _{1-∝/2, n-2} ) to krytyczna wartość t dla poziomu ufności 1-∝ z n-2 stopniami swobody, gdzie n to całkowita liczba obserwacji w naszym zbiorze danych
• (błąd standardowy b ₁ ) jest błędem standardowym b ₁ podanym w wyniku regresji

Dla naszego przykładu, oto jak skonstruować 95% przedział ufności dla B ₁ :

• b ₁ wynosi 93,57 z wyniku regresji.
• Ponieważ używamy 95% przedziału ufności, ∝ = 0,05 i n-2 = 12-2 = 10, więc t _{0,975, 10} wynosi 2,228 zgodnie z tabelą rozkładu t
• (błąd standardowy _b1 ) wynosi 11,45 z wyniku regresji

Zatem nasz 95% przedział ufności dla B ₁ wynosi:

93,57 +/- (2,228) * (11,45) = (68,06, 119,08)

Oznacza to, że mamy 95% pewności, że prawdziwy średni wzrost ceny za każdy dodatkowy metr kwadratowy wyniesie od 68,06 USD do 119,08 USD.

Należy zauważyć, że 0 USD nie mieści się w tym przedziale, więc związek między powierzchnią a ceną jest statystycznie istotny przy poziomie ufności 95%.

Przeprowadzenie testu hipotezy dla nachylenia regresji

Aby przeprowadzić test hipotezy dla nachylenia regresji, wykonujemy pięć standardowych kroków dla każdego testu hipotezy :

Krok 1. Postaw hipotezy.

Hipoteza zerowa (H0): B ₁ = 0

Hipoteza alternatywna: (Ha): B ₁ ≠ 0

Krok 2. Określ poziom istotności, który należy zastosować.

Ponieważ w poprzednim przykładzie skonstruowaliśmy 95% przedział ufności, zastosujemy tutaj równoważne podejście i zdecydujemy się zastosować poziom istotności 0,05.

Krok 3. Znajdź statystykę testową i odpowiadającą jej wartość p.

W tym przypadku statystyka testowa wynosi t = współczynnik b ₁ / błąd standardowy b ₁ przy n-2 stopniach swobody. Z wyniku regresji możemy znaleźć te wartości:

Zatem statystyka testowa t = 92,89 / 13,88 = 6,69.

Używając kalkulatora wyniku T do wartości P z wynikiem 6,69 przy 10 stopniach swobody i teście dwustronnym, wartość p = 0,000 .

Krok 4. Odrzuć lub nie odrzucaj hipotezy zerowej.

Ponieważ wartość p jest poniżej naszego poziomu istotności wynoszącego 0,05, odrzucamy hipotezę zerową.

Krok 5. Interpretacja wyników.

Ponieważ odrzuciliśmy hipotezę zerową, mamy wystarczająco dużo dowodów, aby stwierdzić, że prawdziwy średni wzrost ceny za każdy dodatkowy metr kwadratowy nie wynosi zero.