Współczynnik korelacji pearsona

Współczynnik korelacji Pearsona (znany również jako „współczynnik korelacji momentu iloczynu”) jest miarą liniowego powiązania między dwiema zmiennymi X i Y. Ma wartość od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
• Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
• 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi

Wzór na znalezienie współczynnika korelacji Pearsona

Wzór na znalezienie współczynnika korelacji Pearsona, oznaczonego r , dla próbki danych jest następujący ( za Wikipedią ):

Prawdopodobnie nigdy nie będziesz musiał obliczać tej formuły ręcznie, ponieważ możesz skorzystać z oprogramowania, które zrobi to za Ciebie, ale warto zrozumieć, co dokładnie robi ta formuła, przeglądając przykład.

Załóżmy, że mamy następujący zbiór danych:

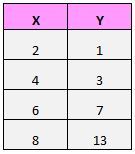
Jeśli wykreślimy te pary (X, Y) na wykresie rozrzutu, będzie to wyglądać następująco:

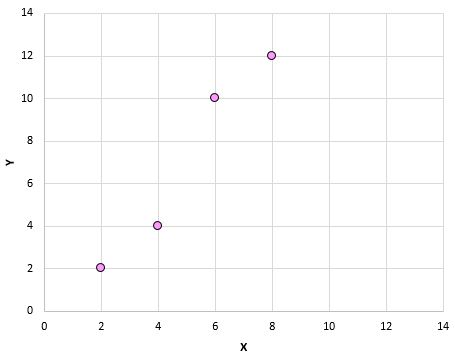
Patrząc na ten wykres rozrzutu, możemy zobaczyć, że istnieje dodatni związek między zmiennymi X i Y: wraz ze wzrostem X Y również ma tendencję do wzrostu. Aby jednak dokładnie określić, jak pozytywnie powiązane są te dwie zmienne, musimy znaleźć współczynnik korelacji Pearsona.

Skupmy się na liczniku wzoru:

Dla każdej pary (X, Y) w naszym zbiorze danych musimy znaleźć różnicę między wartością x a średnią wartością x, różnicę między wartością y a średnią wartością y, a następnie pomnożyć te dwie liczby przez siebie.

Na przykład nasza pierwsza para (X, Y) to (2, 2). Średnia wartość x w tym zestawie danych wynosi 5, a średnia wartość y w tym zestawie danych wynosi 7. Zatem różnica między wartością x tej pary a średnią wartością x wynosi 2 – 5 = -3. Różnica pomiędzy wartością y tej pary a średnią wartością y wynosi 2 – 7 = -5. Następnie, gdy pomnożymy te dwie liczby, otrzymamy -3 * -5 = 15.

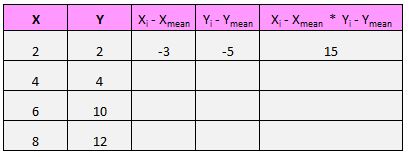
Oto wizualny przegląd tego, co właśnie zrobiliśmy:

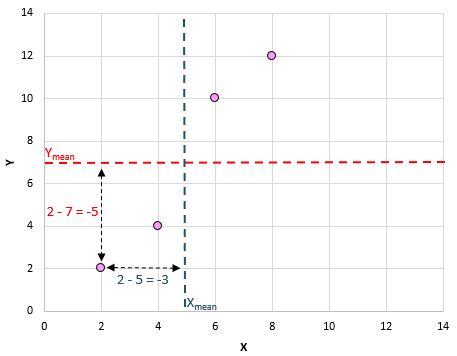
Następnie zrób to dla każdej pary:

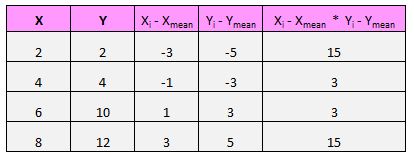
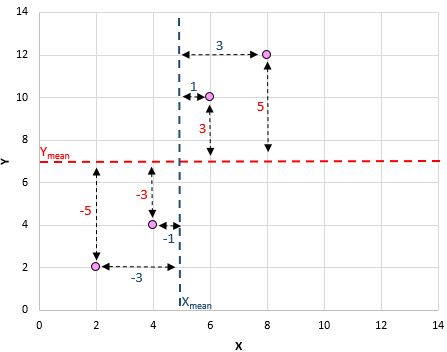
Ostatnim krokiem w celu uzyskania licznika wzoru jest po prostu dodanie wszystkich tych wartości do siebie:

15 + 3 +3 + 15 = 36

Następnie mianownik wzoru każe nam znaleźć sumę wszystkich kwadratów różnic dla x i y, następnie pomnożyć te dwie liczby przez siebie i wyciągnąć pierwiastek kwadratowy:

Zatem najpierw znajdziemy sumę kwadratów różnic dla x i y:

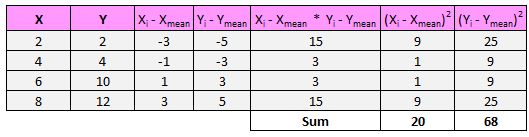
Następnie pomnożymy te dwie liczby przez siebie: 20 * 68 = 1360.

Na koniec weźmiemy pierwiastek kwadratowy: √ 1360 = 36,88

Ustaliliśmy, że licznik wzoru wynosi 36, a mianownik 36,88. Oznacza to, że nasz współczynnik korelacji Pearsona wynosi r = 36 / 36,88 = 0,976

Liczba ta jest bliska 1, co wskazuje, że istnieje silna dodatnia zależność liniowa pomiędzy naszymi zmiennymi X i Y. Potwierdza to zależność, którą zaobserwowaliśmy na wykresie rozrzutu.

Zobacz korelacje

Pamiętaj, że współczynnik korelacji Pearsona mówi nam o rodzaju zależności liniowej (dodatnia, ujemna, brak) pomiędzy dwiema zmiennymi, a także o sile tej zależności (słaba, umiarkowana, silna).

Tworząc wykres rozrzutu dwóch zmiennych, możemy zobaczyć rzeczywisty związek między dwiema zmiennymi. Oto wiele typów zależności liniowych, które możemy zaobserwować:

Silna, pozytywna zależność: wraz ze wzrostem zmiennej na osi x wzrasta również zmienna na osi y. Punkty są blisko siebie skupione, co wskazuje na silny związek.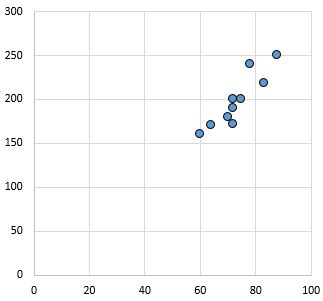

Współczynnik korelacji Pearsona: 0,94

Słaba i pozytywna zależność: wraz ze wzrostem zmiennej na osi x wzrasta również zmienna na osi y. Punkty są dość rozproszone, co wskazuje na słaby związek.

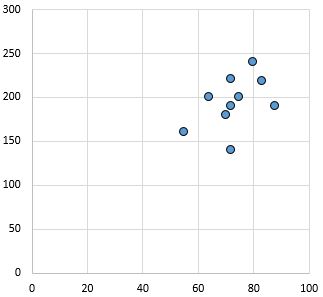
Współczynnik korelacji Pearsona: 0,44

Brak związku: Nie ma wyraźnego związku (dodatniego lub negatywnego) pomiędzy zmiennymi.

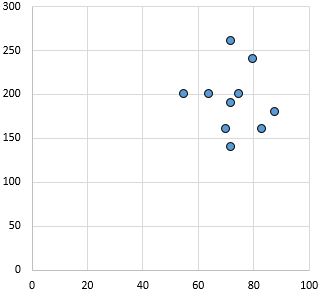
Współczynnik korelacji Pearsona: 0,03

Silna, ujemna zależność: wraz ze wzrostem zmiennej na osi x maleje zmienna na osi y. Punkty są ciasno upakowane, co wskazuje na silny związek.

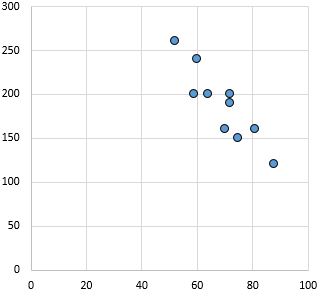
Współczynnik korelacji Pearsona: -0,87

Słaba i ujemna zależność: w miarę wzrostu zmiennej na osi x maleje zmienna na osi y. Punkty są dość rozproszone, co wskazuje na słaby związek.

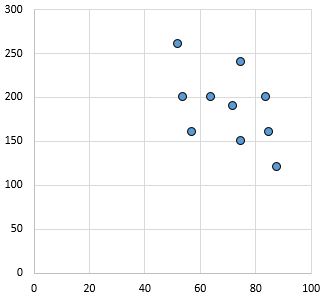
Współczynnik korelacji Pearsona: – 0,46

Badanie istotności współczynnika korelacji Pearsona

Kiedy znajdujemy współczynnik korelacji Pearsona dla zbioru danych, często pracujemy z próbką danych z większej populacji . Oznacza to, że możliwe jest znalezienie niezerowej korelacji dla dwóch zmiennych, nawet jeśli w rzeczywistości są one nieskorelowane w całej populacji.

Załóżmy na przykład, że tworzymy wykres rozrzutu dla zmiennych X i Y dla każdego punktu danych w całej populacji i wygląda on następująco:

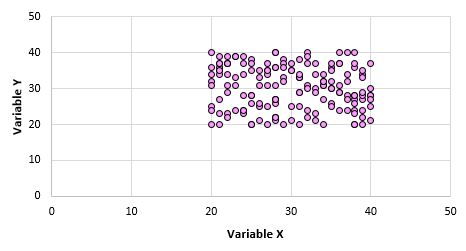
Jest oczywiste, że te dwie zmienne nie są ze sobą skorelowane. Możliwe jest jednak, że biorąc z populacji próbę 10 punktów, wybierzemy następujące punkty:

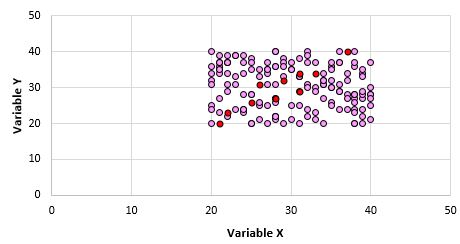
Widzimy, że współczynnik korelacji Pearsona dla tej próby punktów wynosi 0,93, co wskazuje na silną dodatnią korelację, mimo że korelacja populacyjna wynosi zero.

Aby sprawdzić, czy korelacja między dwiema zmiennymi jest istotna statystycznie, czy nie, możemy znaleźć następującą statystykę testową:

Statystyka testowa T = r * √ (n-2) / (1-r ² )

gdzie n to liczba par w naszej próbie, r to współczynnik korelacji Pearsona, a statystyka testu T ma rozkład z n-2 stopniami swobody.

Przyjrzyjmy się przykładowi testowania istotności współczynnika korelacji Pearsona.

Przykład

Poniższy zbiór danych przedstawia wzrost i wagę 12 osobników:

Poniższy wykres rozrzutu pokazuje wartość tych dwóch zmiennych:

Współczynnik korelacji Pearsona dla tych dwóch zmiennych wynosi r = 0,836.

Statystyka testowa T = 0,836 * √ (12 -2) / (1-0,836 ² ) = 4,804.

Według naszego kalkulatora rozkładu t , wynik 4,804 przy 10 stopniach swobody ma wartość p wynoszącą 0,0007. Ponieważ 0,0007 < 0,05, możemy stwierdzić, że korelacja między masą ciała a wzrostem w tym przykładzie jest istotna statystycznie przy alfa = 0,05.

Środki ostrożności

Chociaż współczynnik korelacji Pearsona może być przydatny do stwierdzenia, czy dwie zmienne mają powiązanie liniowe, musimy pamiętać o trzech rzeczach, interpretując współczynnik korelacji Pearsona:

1. Korelacja nie implikuje związku przyczynowego. To nie dlatego, że dwie zmienne są ze sobą skorelowane, jedna koniecznie powoduje , że druga pojawia się częściej lub rzadziej. Klasycznym tego przykładem jest pozytywna korelacja między sprzedażą lodów a atakami rekinów. Kiedy w określonych porach roku sprzedaż lodów wzrasta, ataki rekinów również się zwiększają.

Czy to oznacza, że jedzenie lodów powoduje ataki rekinów? Oczywiście nie! Oznacza to po prostu, że latem zwiększa się spożycie lodu i ataki rekinów, ponieważ latem lód jest bardziej popularny i więcej ludzi wpływa do oceanu latem.

2. Korelacje są wrażliwe na wartości odstające. Skrajna wartość odstająca może znacząco zmienić współczynnik korelacji Pearsona. Rozważ poniższy przykład:

Zmienne X i Y mają współczynnik korelacji Pearsona równy 0,00 . Ale wyobraźmy sobie, że w zbiorze danych mamy wartość odstającą:

Jednakże współczynnik korelacji Pearsona dla tych dwóch zmiennych wynosi 0,878 . Ta jedna wartość odstająca zmienia wszystko. Dlatego też obliczając korelację dla dwóch zmiennych, dobrym pomysłem jest wizualizacja zmiennych za pomocą wykresu rozrzutu w celu sprawdzenia, czy nie występują wartości odstające.

3. Współczynnik korelacji Pearsona nie oddaje nieliniowych zależności pomiędzy dwiema zmiennymi. Wyobraźmy sobie, że mamy dwie zmienne powiązane następującą zależnością:

Współczynnik korelacji Pearsona dla tych dwóch zmiennych wynosi 0,00, ponieważ nie mają one związku liniowego. Jednakże te dwie zmienne mają związek nieliniowy: wartości y to po prostu wartości x podniesione do kwadratu.

Korzystając ze współczynnika korelacji Pearsona, należy pamiętać, że po prostu testujesz, czy dwie zmienne są liniowo powiązane. Nawet jeśli współczynnik korelacji Pearsona mówi nam, że dwie zmienne nie są skorelowane, nadal mogą mieć pewien rodzaj nieliniowej zależności. Jest to kolejny powód, dla którego przydatne jest utworzenie wykresu rozrzutu podczas analizowania relacji między dwiema zmiennymi: może to pomóc w wykryciu zależności nieliniowej.