Jak wykonać test z w dwóch proporcjach w sas-ie

Do określenia, czy istnieje statystycznie istotna różnica między dwiema proporcjami populacji, stosuje się test z dwóch proporcji.

W tym teście zastosowano następującą hipotezę zerową:

• H ₀ : μ ₁ = μ ₂ (oba proporcje populacji są równe)

Hipoteza alternatywna może być dwustronna, lewa lub prawa:

• H ₁ (dwustronny): π ₁ ≠ π ₂ (oba proporcje populacji nie są równe)
• H ₁ (po lewej): π ₁ < π ₂ (odsetek populacji 1 jest mniejszy niż odsetek populacji 2)
• H ₁ (po prawej): π ₁ > π ₂ (odsetek populacji 1 jest większy niż odsetek populacji 2)

Do obliczenia statystyki testu z używamy następującego wzoru:

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ )

gdzie p ₁ i p ₂ to proporcje próbek, n ₁ i n ₂ to liczebność próbek, a p to całkowity udział zbiorczy obliczony w następujący sposób:

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ + n ₂ )

Jeśli wartość p odpowiadająca statystyce testu z jest mniejsza niż wybrany poziom istotności (najczęściej wybierane wartości to 0,10, 0,05 i 0,01), wówczas można odrzucić hipotezę zerową.

Poniższy przykład pokazuje, jak wykonać test Z dwóch proporcji w SAS-ie.

Przykład: Test dwóch proporcji Z w SAS

Załóżmy, że chcemy wiedzieć, czy istnieje różnica między odsetkiem mieszkańców popierających określone prawo w hrabstwie A a odsetkiem mieszkańców popierających prawo w hrabstwie B.

Aby to sprawdzić, zbieramy losową próbę 50 mieszkańców z każdego powiatu i liczymy, ilu z nich popiera prawo.

Poniższy kod pokazuje, jak utworzyć zbiór danych podsumowujący liczbę mieszkańców popierających prawo w każdym powiecie:

 /*create dataset*/
data my_data;
    input county $status $count;
    datalines ;
A Bracket 34
A Reject 16
B Bracket 29
B Reject 21
;
run ;

/*view dataset*/
proc print data =my_data;

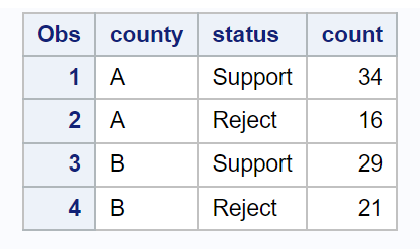
Możemy następnie użyć instrukcji PROC FREQ z opcją Riskdiff (equal var = null), aby wykonać test z dwóch proporcji:

 /*perform two proportion z-test*/
proc freq data =my_data;
    weightcount ;
    county tables * status / riskdiff ( equal var = null);
run ; 

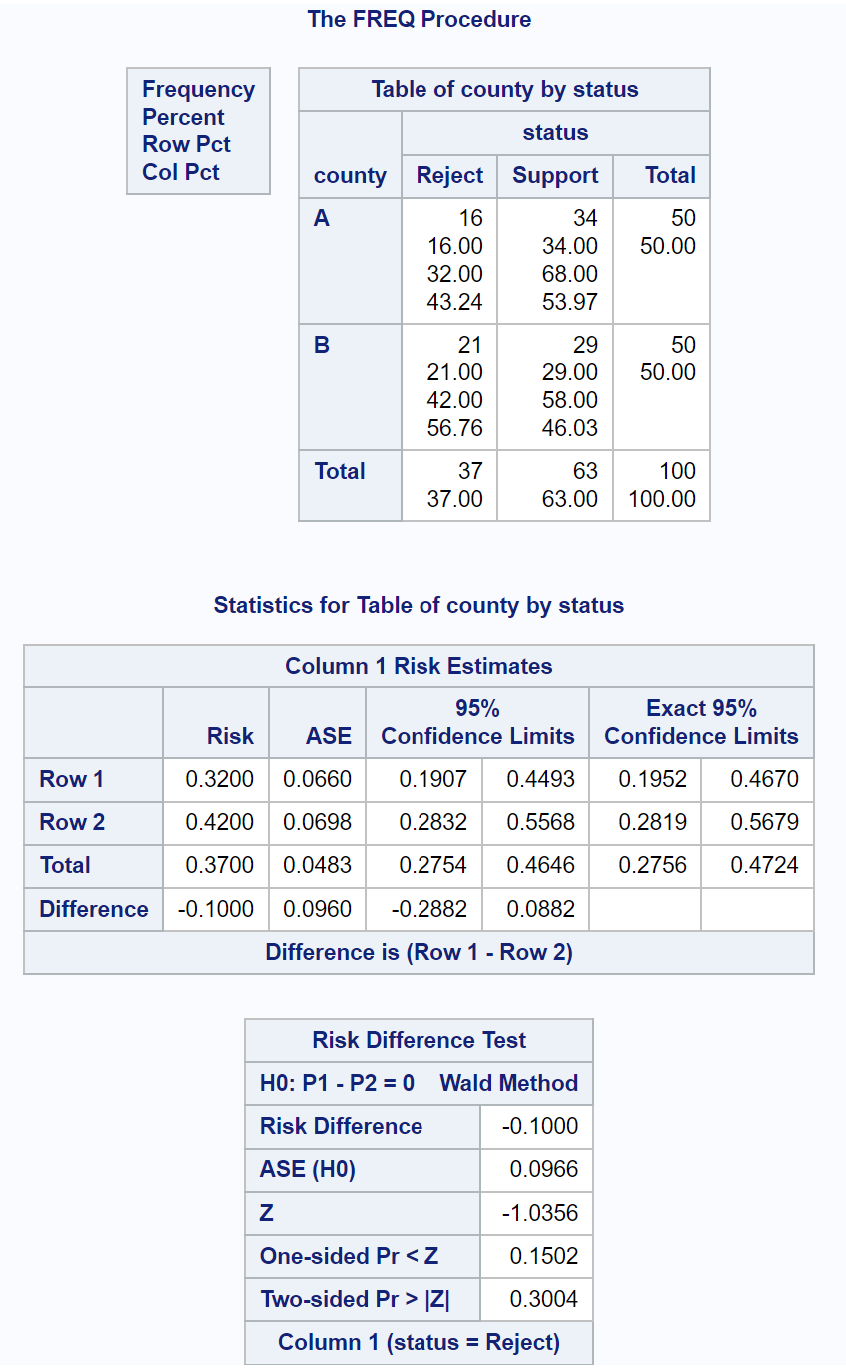
W tabeli wyników testu różnicy ryzyka możemy zobaczyć następujące informacje:

• Statystyka testu Z: -1,0356
• Dwustronna wartość p: 0,3004

W tym konkretnym teście z dwóch proporcji wykorzystano następujące założenia:

• H ₀ : π ₁ = π ₂ (oba proporcje populacji są równe)
• H ₁ : π ₁ ≠ π ₂ (oba proporcje populacji nie są równe)

Ponieważ wartość p na wyjściu jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.

Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że odsetek mieszkańców popierających tę ustawę różni się w obu hrabstwach.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne popularne testy statystyczne w SAS-ie:

Jak wykonać test t dla jednej próby w SAS
Jak wykonać test t dla dwóch próbek w SAS
Jak wykonać test t dla sparowanych próbek w SAS