Excel: oblicz przedział ufności dla współczynnika regresji

W modelu regresji liniowej współczynnik regresji informuje nas o średniej zmianiezmiennej odpowiedzi powiązanej ze wzrostem o jedną jednostkę zmiennej predykcyjnej.

Do obliczenia przedziału ufności dla współczynnika regresji możemy użyć następującego wzoru:

Przedział ufności dla β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

Złoto:

•   b ₁ = współczynnik regresji pokazany w tabeli regresji
• t _{1-∝/2, n-2} = Krytyczna wartość t dla poziomu ufności 1-∝ z n-2 stopniami swobody, gdzie n jest całkowitą liczbą obserwacji w naszym zbiorze danych
• se(b ₁ ) = Błąd standardowy b ₁ pokazany w tabeli regresji

Poniższy przykład pokazuje, jak obliczyć przedział ufności dla współczynnika regresji w programie Excel.

Przykład: Przedział ufności dla współczynnika regresji w programie Excel

Załóżmy, że chcemy dopasować prosty model regresji liniowej, wykorzystując przestudiowane godziny jako zmienną predykcyjną i wyniki egzaminów jako zmienną odpowiedzi dla 15 uczniów w określonej klasie:

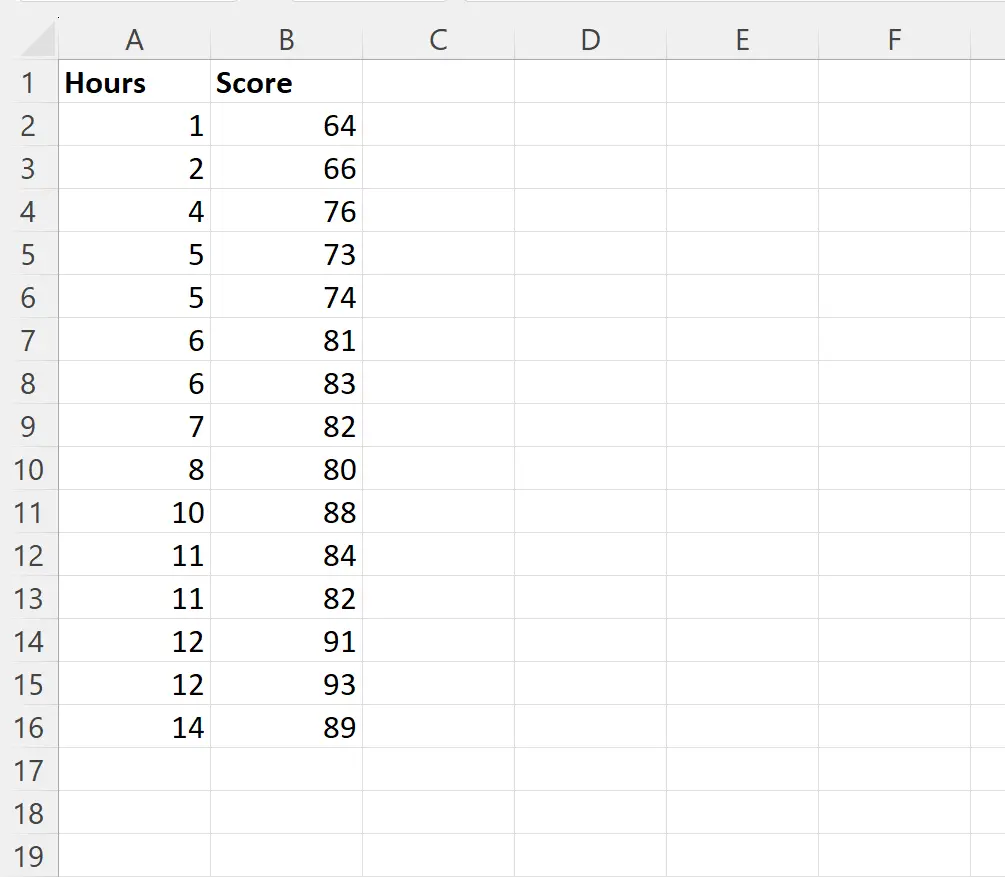
Możemy wpisać następującą formułę w komórce D2, aby przeprowadzić prostą regresję liniową, wykorzystując wartości z kolumny Godziny jako zmienną predykcyjną i wartości z kolumny Wynik jako zmienną odpowiedzi:

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

Należy zauważyć, że pierwszy argument PRAWDA informuje program Excel, aby normalnie obliczył punkt wyrazu równania regresji, nie wymuszając jego wartości zerowej.

Drugi argument TRUE informuje program Excel, aby oprócz współczynników wygenerował dodatkowe statystyki regresji.

Poniższy zrzut ekranu przedstawia wynik tej formuły (wyjaśniamy, co reprezentuje każda wartość wyjściowa, w czerwonym tekście pod wynikami):

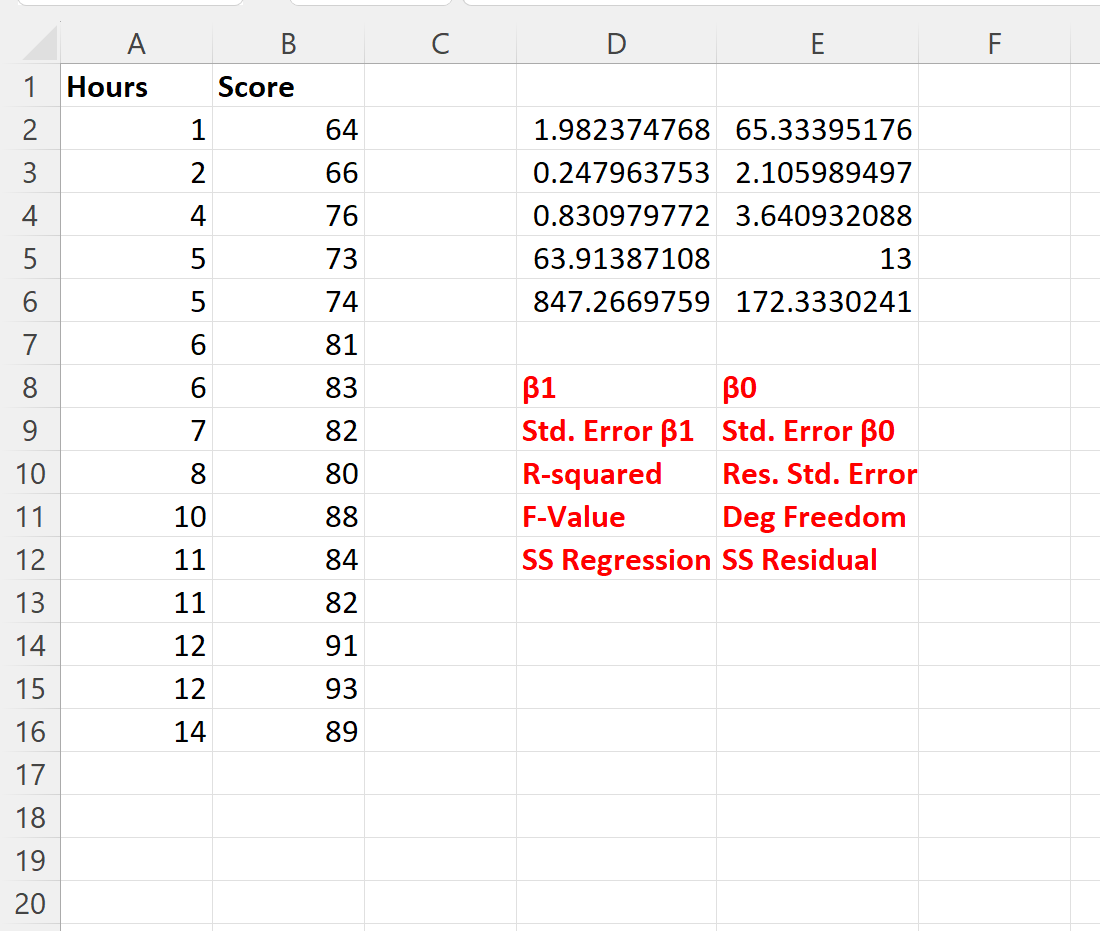
Korzystając ze współczynników regresji, możemy zapisać dopasowane równanie regresji w następujący sposób:

Wynik = 65,334 + 1,982*(Godziny nauki)

Należy zauważyć, że współczynnik regresji dla godzin wynosi 1,982 .

To mówi nam, że każda dodatkowa godzina spędzona na nauce wiąże się ze średnim wzrostem wyniku egzaminu o 1982 .

Aby obliczyć 95% przedział ufności dla współczynnika regresji, możemy wpisać w komórkach H2 i H3 następujące wzory:

• H2: = D2 – T.INV.2T(0,05, E5)*D3
• H3: = D2 + T.INV.2T(0,05, E5)*D3

Poniższy zrzut ekranu pokazuje, jak w praktyce korzystać z tych formuł:

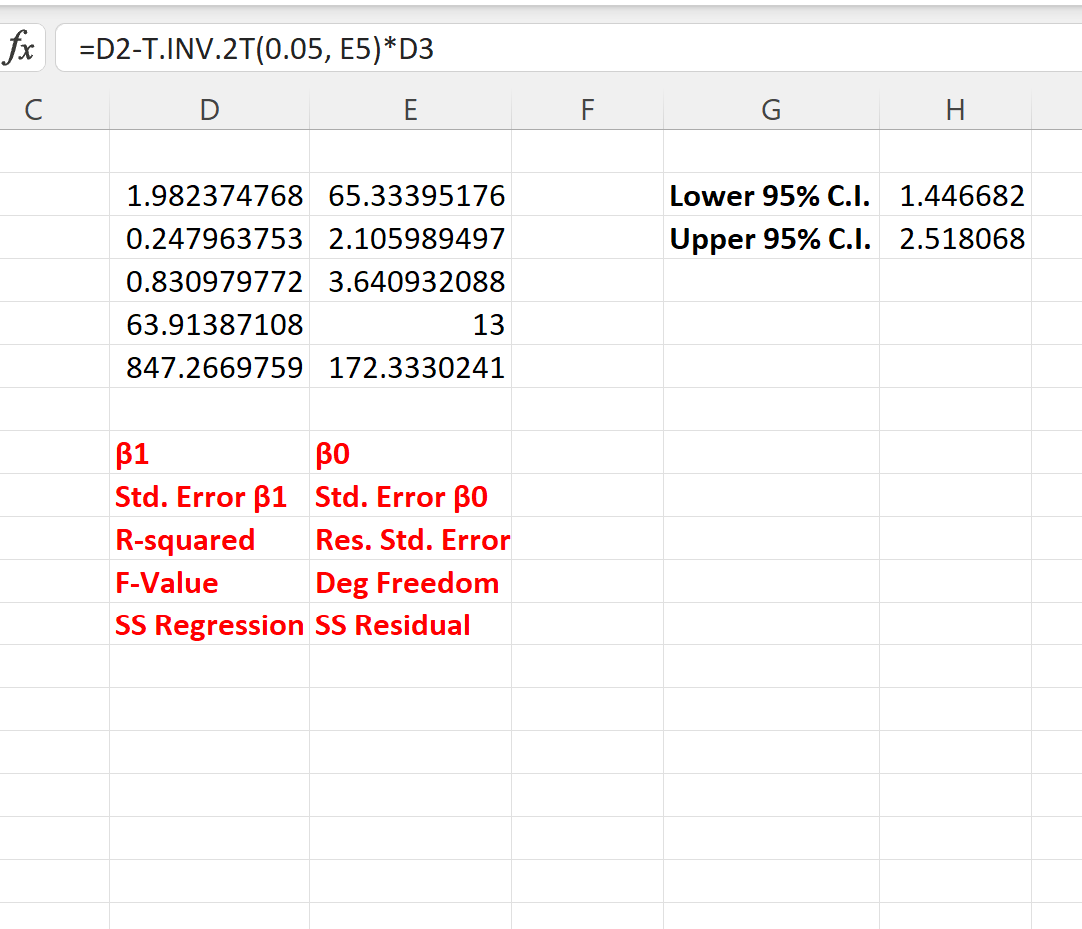
95% przedział ufności dla współczynnika regresji wynosi [1,446, 2,518] .

Ponieważ ten przedział ufnościnie zawiera wartości 0 , możemy stwierdzić, że istnieje statystycznie istotny związek pomiędzy przepracowanymi godzinami a oceną z egzaminu.

Możemy również potwierdzić, że jest to prawidłowe, ręcznie obliczając 95% przedział ufności dla współczynnika regresji:

• 95% CI dla β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )
• 95% CI dla β ₁ : 1,982 ± t _{0,975, 15-2} * 0,248
• 95% CI dla β ₁ : 1,982 ± 2,1604 * 0,248
• 95% CI dla β ₁ : [1,446, 2,518]

95% przedział ufności dla współczynnika regresji wynosi [1,446, 2,518] .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w programie Excel:

Jak wykonać prostą regresję liniową w programie Excel
Jak wykonać wielokrotną regresję liniową w programie Excel
Jak interpretować wartości P w wynikach regresji w programie Excel