Jak sprawdzić założenia anova

Jednoczynnikowa ANOVA jest testem statystycznym stosowanym do określenia, czy istnieje istotna różnica pomiędzy średnimi z trzech lub więcej niezależnych grup.

Oto przykład, kiedy możemy zastosować jednokierunkową ANOVA:

Losowo dzielisz klasę składającą się z 90 uczniów na trzy grupy po 30 osób. Każda grupa przez miesiąc wykorzystuje inną technikę nauki, aby przygotować się do egzaminu. Pod koniec miesiąca wszyscy uczniowie przystępują do tego samego egzaminu.

Chcesz wiedzieć, czy technika nauki ma wpływ na wyniki egzaminu. Wykonujesz zatem jednoczynnikową analizę ANOVA , aby określić, czy istnieje statystycznie istotna różnica między średnimi wynikami trzech grup.

Zanim będziemy mogli przeprowadzić jednokierunkową analizę ANOVA, musimy najpierw sprawdzić, czy spełnione są trzy założenia.

1. Normalność – każda próba została pobrana z populacji o rozkładzie normalnym.

2. Równe wariancje – wariancje populacji, z których pobierane są próbki, są równe.

3. Niezależność – obserwacje w obrębie każdej grupy są od siebie niezależne, a obserwacje w obrębie grup uzyskano w drodze losowego doboru próby.

Jeżeli te założenia nie zostaną spełnione, wyniki naszej jednokierunkowej analizy wariancji mogą nie być wiarygodne.

W tym artykule wyjaśniamy, jak sprawdzić te założenia i co zrobić, jeśli któreś z nich zostanie naruszone.

Założenie nr 1: normalność

ANOVA zakłada, że każda próbka została pobrana z populacji o rozkładzie normalnym.

Jak sprawdzić tę hipotezę w R:

Aby zweryfikować tę hipotezę, możemy zastosować dwa podejścia:

• Wizualnie zweryfikuj hipotezę za pomocą histogramów lub wykresów QQ .
• Zweryfikuj hipotezę za pomocą formalnych testów statystycznych, takich jak Shapiro-Wilk, Kołmogorow-Smironow, Jarque-Barre lub D’Agostino-Pearson.

Załóżmy na przykład, że rekrutujemy 90 osób do udziału w eksperymencie dotyczącym utraty wagi, podczas którego losowo przydzielamy 30 osób do udziału w Programie A, Programie B lub Programie C przez jeden miesiąc. Aby sprawdzić, czy program ma wpływ na utratę wagi, chcemy wykonać jednokierunkową ANOVA. Poniższy kod ilustruje sposób sprawdzenia założenia normalności przy użyciu histogramów, wykresów QQ i testu Shapiro-Wilka.

1. Zamontuj model ANOVA.

 #make this example reproducible
set.seed(0)

#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. Utwórz histogram wartości odpowiedzi.

 #create histogram
hist(data$weight_loss)

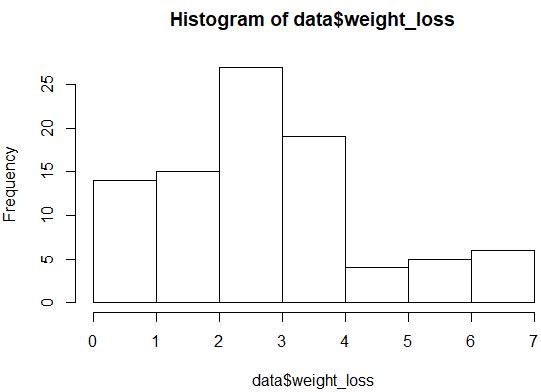
Rozkład nie wygląda na rozkład normalny (np. nie ma kształtu „dzwonu”), ale możemy również utworzyć wykres QQ, aby jeszcze raz przyjrzeć się rozkładowi.

3. Utwórz wykres QQ reszt

 #create QQ plot to compare this dataset to a theoretical normal distribution
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals) 

Ogólnie rzecz biorąc, jeśli punkty danych leżą na prostej ukośnej na wykresie QQ, wówczas zbiór danych prawdopodobnie ma rozkład normalny. W tym przypadku widać zauważalne odchylenie od linii na końcach, co może wskazywać, że dane nie mają rozkładu normalnego.

4. Wykonaj test Shapiro-Wilka na normalność.

 #Conduct Shapiro-Wilk Test for normality
shapiro. test (data$weight_loss)

#Shapiro-Wilk normality test
#
#data: data$weight_loss
#W = 0.9587, p-value = 0.005999

Test Shapiro-Wilka sprawdza hipotezę zerową, że próbki pochodzą z rozkładu normalnego, w porównaniu z hipotezą alternatywną, że próbki nie pochodzą z rozkładu normalnego. W tym przypadku wartość p testu wynosi 0,005999 , czyli jest niższa niż poziom alfa wynoszący 0,05. Sugeruje to, że próbki nie mają rozkładu normalnego.

Co zrobić, jeśli to założenie nie jest przestrzegane:

Ogólnie rzecz biorąc, jednoczynnikową ANOVA uważa się za dość odporną na naruszenia założenia normalności, o ile rozmiary próbek są wystarczająco duże.

Ponadto, jeśli masz wyjątkowo duże próbki, testy statystyczne, takie jak test Shapiro-Wilka, prawie zawsze wykażą, że Twoje dane nie są normalne. Z tego powodu często najlepiej jest wizualnie sprawdzić dane za pomocą wykresów, takich jak histogramy i wykresy QQ. Wystarczy spojrzeć na wykresy, aby uzyskać całkiem niezłe pojęcie o tym, czy dane mają rozkład normalny, czy nie.

Jeśli założenie o normalności zostanie poważnie naruszone lub po prostu chcesz zachować się bardzo konserwatywnie, masz dwie możliwości:

(1) Przekształć wartości odpowiedzi swoich danych, aby rozkłady były bardziej normalne.

(2) Wykonaj równoważny test nieparametryczny, taki jak test Kruskala-Wallisa , który nie wymaga założenia normalności.

Założenie nr 2: równa wariancja

ANOVA zakłada, że wariancje populacji, z których pobierane są próbki, są równe.

Jak sprawdzić tę hipotezę w R:

Możemy zweryfikować tę hipotezę w R, stosując dwa podejścia:

• Wizualnie zweryfikuj hipotezę za pomocą wykresów pudełkowych.
• Sprawdź hipotezę za pomocą formalnych testów statystycznych, takich jak test Bartletta.

Poniższy kod demonstruje, jak to zrobić, korzystając z tego samego fałszywego zestawu danych dotyczących utraty wagi, który utworzyliśmy wcześniej.

1. Utwórz wykresy pudełkowe.

 #Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)

Różnicę w utracie masy ciała w każdej grupie można zaobserwować na podstawie długości każdego wykresu pudełkowego. Im dłuższe pudełko, tym większa wariancja. Na przykład widzimy, że wariancja jest nieco większa w przypadku uczestników Programu C w porównaniu z Programem A i Programem B.

2. Wykonaj test Bartletta.

 #Create box plots that show distribution of weight loss for each group
bartlett. test (weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data: weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

Test Bartletta sprawdza hipotezę zerową, że próbki mają równe wariancje, w porównaniu z alternatywną hipotezą, że próbki nie mają równych wariancji. W tym przypadku wartość p testu wynosi 0,01599 , czyli jest niższa niż poziom alfa wynoszący 0,05. Sugeruje to, że nie wszystkie próbki mają tę samą wariancję.

Co zrobić, jeśli to założenie nie jest przestrzegane:

Ogólnie rzecz biorąc, jednoczynnikową ANOVA uważa się za dość odporną na naruszenia założenia o równych wariancjach, o ile każda grupa ma tę samą wielkość próby.

Jeśli jednak rozmiary próbek nie są takie same i to założenie zostanie poważnie naruszone, można zamiast tego przeprowadzić test Kruskala-Wallisa , który jest nieparametryczną wersją jednokierunkowej analizy ANOVA.

Założenie nr 3: Niezależność

ANOVA zakłada:

• Obserwacje każdej grupy są niezależne od obserwacji wszystkich pozostałych grup.
• Obserwacje w obrębie każdej grupy uzyskano na podstawie losowej próby.

Jak zweryfikować tę hipotezę:

Nie ma formalnego testu, za pomocą którego można sprawdzić, czy obserwacje w każdej grupie są niezależne i czy zostały uzyskane na próbie losowej. Jedynym sposobem spełnienia tego założenia jest zastosowanie projektu losowego.

Co zrobić, jeśli to założenie nie jest przestrzegane:

Niestety, jeśli to założenie nie jest spełnione, niewiele można zrobić. Mówiąc najprościej, jeśli dane zostały zebrane w taki sposób, że obserwacje w każdej grupie nie były niezależne od obserwacji w innych grupach, lub jeśli obserwacje w obrębie każdej grupy nie zostały uzyskane w procesie randomizowanym, wyniki ANOVA nie będą wiarygodne .

Jeśli to założenie nie jest spełnione, najlepszym rozwiązaniem jest odtworzenie eksperymentu przy użyciu losowego projektu.

Dalsza lektura:

Jak wykonać jednokierunkową ANOVA w R
Jak wykonać jednokierunkową ANOVA w programie Excel