Co to jest próbka reprezentatywna i dlaczego jest ważna?

W statystyce często jesteśmy zainteresowani badaniem cech konkretnych populacji. Na przykład możemy być zainteresowani studiowaniem:

• Ogólna satysfakcja z pracy inżynierów mechaników w danym mieście.
• Preferencje polityczne jednostek w danym powiecie.
• Rozkład wieku osób w danym kraju.
• Preferencje filmowe uczniów danej szkoły.

W każdym z tych przykładów chcemy lepiej zrozumieć określonąpopulację .

Populacja: Cała grupa osób, którą chcesz badać.

Niestety zbieranie danych na temat każdego osobnika w populacji może być kosztowne i czasochłonne. Dlatego badacze zazwyczaj zbierają dane na próbie populacji, a następnie uogólniają wyniki tej próby na całą populację.

Próba: podzbiór populacji.

Załóżmy na przykład, że chcemy poznać preferencje dotyczące filmów uczniów w pewnej szkole, do której uczęszcza ogółem 1000 uczniów. Ponieważ badanie każdego ucznia indywidualnie zajęłoby zbyt dużo czasu, moglibyśmy zamiast tego wybrać losową próbę 100 uczniów i zapytać ich o ich preferencje.

1000 uczniów reprezentuje populację, natomiast 100 losowo wybranych uczniów reprezentuje próbę. Po zebraniu danych dla próby 100 uczniów możemy uogólnić te wyniki na ogólną populację 1000 uczniów, ale tylko wtedy, gdy nasza próba jest reprezentatywna dla naszej populacji .

Próba reprezentatywna: Próba, w której cechy jednostek są ściśle zgodne z cechami całej populacji.

Idealnie byłoby, gdyby nasza próba przypominała „mini wersję” naszej populacji. Zatem jeśli ogólna populacja uczniów składa się z 50% dziewcząt i 50% chłopców, nasza próba nie byłaby reprezentatywna, gdyby obejmowała 90% chłopców i tylko 10% dziewcząt.

Lub, jeśli ogólna populacja składa się w równych częściach ze studentów pierwszego roku, drugiego roku, juniorów i seniorów, wówczas nasza próba nie byłaby reprezentatywna, gdyby obejmowała tylko studentów pierwszego roku.

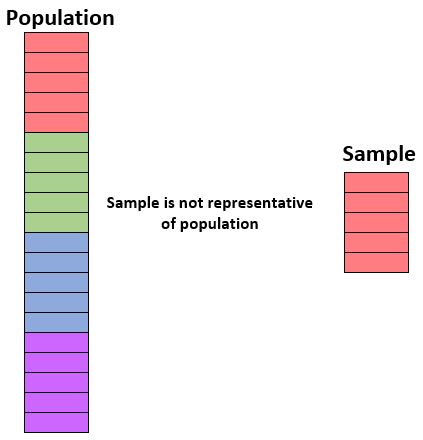
Znaczenie uzyskania reprezentatywnej próbki

Powodem, dla którego potrzebujemy reprezentatywnej próby, jest to, że możemy z całą pewnością uogólnić wyniki z próby na populację.

Załóżmy na przykład, że chcemy wiedzieć, jaki procent uczniów w określonej szkole preferuje „dramat” jako swój ulubiony gatunek filmowy. Jeżeli całkowita populacja uczniów składa się z 50% chłopców i 50% dziewcząt, wówczas próba składająca się z 90% chłopców i 10% dziewcząt może prowadzić do stronniczych wyników, jeśli znacznie mniej chłopców preferuje teatr jako swój ulubiony gatunek.

Lub, jeśli całkowita populacja składa się z równej mieszanki studentów pierwszego roku, drugiego roku, juniorów i seniorów, wówczas próba obejmująca wyłącznie studentów pierwszego roku może również prowadzić do stronniczych wyników, jeśli młodsi studenci (np. studenci pierwszego roku) mają tendencję do preferowania teatru w znacznie większym stopniu niż studenci pierwszego roku. starsi uczniowie.

Jeżeli cechy osób w naszej próbie nie odpowiadają ściśle cechom osób w całej populacji, nie możemy z całą pewnością uogólnić wyników z próby na całą populację.

Jak uzyskać reprezentatywną próbkę

Aby zmaksymalizować szansę na uzyskanie reprezentatywnej próbki, podczas jej pozyskiwania musimy skupić się na dwóch rzeczach:

1. Zastosuj odpowiednią metodę pobierania próbek.

Próbkę populacji można uzyskać na wiele sposobów , ale poniżej przedstawiamy trzy metody, dzięki którym można uzyskać próbkę reprezentatywną:

Prosta próbka losowa: wybierz losowo osoby za pomocą generatora liczb losowych lub środków doboru losowego.

• Przykład: Przypisz numer 1000 uczniom. Następnie użyj generatora liczb losowych, aby wybrać 100 liczb losowych i użyj odpowiednich uczniów jako członków próby.
• Zaleta: Proste próbki losowe są na ogół reprezentatywne dla populacji będącej przedmiotem zainteresowania, ponieważ każdy członek ma równe szanse na włączenie do próby.

Systematyczna próba losowa: umieść każdego członka populacji w określonej kolejności. Wybierz losowy punkt początkowy i wybierz jednego członka ^spośród n, który będzie częścią próbki.

• Przykład: Utwórz listę alfabetyczną na podstawie nazwisk wszystkich 1000 uczniów, losowo wybierz punkt początkowy i wybierz co dziesiątego ucznia do próby.
• Zaleta: Systematyczne próby losowe są na ogół reprezentatywne dla populacji będącej przedmiotem zainteresowania, ponieważ każdy członek ma równe szanse na włączenie do próby.

Stratyfikowana próba losowa: podziel populację na grupy. Wybierz losowo kilku członków z każdej grupy, którzy staną się częścią próby.

• Przykład: Podziel wszystkich uczniów według ich poziomu: studenci pierwszego roku, studenci drugiego roku, juniorzy i seniorzy. Wybierz losowo 25 uczniów z każdej klasy, którzy staną się częścią próby.
• Zaleta: Warstwowe próby losowe zapewniają, że w próbie znajdzie się taka sama liczba uczniów z każdej klasy.

2. Upewnij się, że próbka jest wystarczająco duża.

Oprócz zastosowania odpowiedniej metody próbkowania ważne jest, aby próba była wystarczająco duża, abyśmy mieli wystarczającą ilość danych, aby móc uogólniać na większą populację.

Na przykład próba składająca się z ośmiu uczniów – jednego chłopca i jednej dziewczynki z każdej klasy – może reprezentować miniwersję populacji jako całości, ale prawdopodobnie nie jest wystarczająco duża, aby uchwycić całą zmienność, która naturalnie występuje w odpowiedziach uczniów .

Jak duża powinna być Twoja próbka?

Zależy to od następujących czynników:

• Wielkość populacji: Ogólnie rzecz biorąc, im większa wielkość populacji, tym większa powinna być próba. Na przykład, jeśli chcesz uogólnić wyniki na cały kraj, a nie na pojedyncze miasto, będziesz potrzebować znacznie większej próby.
• Poziom ufności: Jak pewny chcesz być, że prawdziwa wartość populacji, którą jesteś zainteresowany, mieści się w Twoim przedziale ufności. Typowe poziomy ufności obejmują 90%, 95% i 99%. Im wyższy poziom ufności, tym większa powinna być próbka.
• Margines błędu: ile błędów jesteś skłonny tolerować. Żadna próbka nie będzie idealna, więc musisz zaakceptować przynajmniej pewną ilość błędów. Większość badań naukowych podaje swoje wyniki z marginesem błędu, na przykład „40% studentów stwierdziło, że teatr jest ich ulubionym gatunkiem filmowym, z marginesem błędu wynoszącym +/- 5%”. » Im niższy margines błędu, tym mniejsza powinna być próbka.

W Internecie dostępnych jest wiele kalkulatorów wielkości próby, które pomogą Ci określić wielkość próby na podstawie tych czynników. Ten kalkulator firmy Survey Monkey jest szczególnie łatwy w użyciu.

Rzeczy, o których warto pamiętać

Nawet jeśli zastosujesz właściwą metodę pobierania próbek i upewnisz się, że próbka jest wystarczająco duża, pamiętaj o następujących kwestiach:

• Zawsze będzie występował błąd próbkowania. Próba nigdy nie będzie idealnie reprezentatywna dla całej populacji.
• Ogólnie rzecz biorąc, im większa próba, tym bardziej jest ona reprezentatywna dla populacji.
• Należy zrównoważyć wielkość próby ze zmiennymi rzeczywistymi, takimi jak czas i koszt. Większa próbka może z większym prawdopodobieństwem reprezentować całą populację, ale jej uzyskanie może być bardziej kosztowne i czasochłonne.