Jak czytać tabelę rozkładu chi-kwadrat

W tym samouczku wyjaśniono, jak czytać i interpretować wykres rozkładu chi-kwadrat.

Co to jest tabela rozkładu chi-kwadrat?

Tabela rozkładu Chi-kwadrat to tabela pokazująca wartości krytyczne rozkładu Chi-kwadrat. Aby skorzystać z tabeli rozkładu Chi-kwadrat, wystarczy znać dwie wartości:

• Stopnie swobody dla testu Chi-kwadrat
• Poziom alfa testu (często wybierane wartości to 0,01, 0,05 i 0,10)

Poniższy obraz przedstawia pierwsze 20 wierszy tabeli rozkładu chi-kwadrat, ze stopniami swobody po lewej stronie tabeli i poziomami alfa u góry tabeli:

Uwaga: pełną tabelę rozkładu Chi-kwadrat z większą liczbą stopni swobody można znaleźć tutaj.

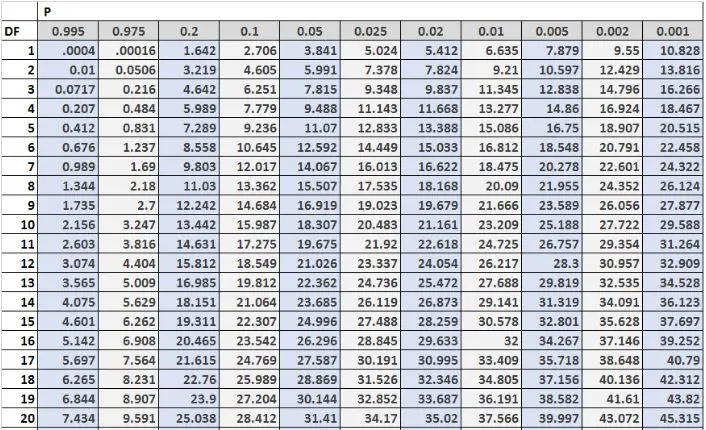
Wartości krytyczne w tabeli są często porównywane ze statystykami testowymi testu Chi-kwadrat. Jeżeli statystyka testowa jest większa od wartości krytycznej podanej w tabeli, wówczas można odrzucić hipotezę zerową testu Chi-kwadrat i stwierdzić, że wyniki testu są istotne statystycznie.

Przykłady wykorzystania tablicy rozkładu chi-kwadrat

Pokażemy, jak używać tabeli rozkładu Chi-kwadrat z trzema następującymi typami testów Chi-kwadrat:

• Test chi-kwadrat niezależności
• Test chi-kwadrat na dobroć dopasowania
• Test chi-kwadrat na jednorodność

Test chi-kwadrat niezależności

Testu chi-kwadrat niezależności używamy , gdy chcemy sprawdzić, czy istnieje istotny związek między dwiema zmiennymi kategorycznymi.

Przykład: Załóżmy, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej. Bierzemy prostą losową próbę 500 wyborców i pytamy ich o preferencje dotyczące partii politycznych. Stosując poziom istotności 0,05, przeprowadzamy test chi-kwadrat, aby ustalić, czy płeć jest powiązana z preferencjami partii politycznych. Wyniki badania prezentuje poniższa tabela:

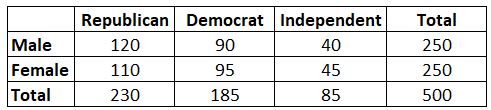
Okazuje się, że statystyka testowa dla tego testu Chi-kwadrat wynosi 0,864.

Następnie możemy znaleźć krytyczną wartość testową w tabeli rozkładu Chi-kwadrat. Stopnie swobody są równe (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2, a problem powiedział nam, że powinniśmy zastosować poziom alfa równy 0,05. zgodnie z tabelą rozkładu chi-kwadrat wartość krytyczna testu wynosi 5,991 .

Ponieważ nasza statystyka testowa jest mniejsza niż wartość krytyczna, nie możemy odrzucić hipotezy zerowej. Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że istnieje związek między płcią a preferencjami partii politycznych.

Test chi-kwadrat na dobroć dopasowania

Testu dobroci dopasowania chi-kwadrat używamy, gdy chcemy sprawdzić, czy zmienna kategoryczna ma rozkład hipotetyczny.

Przykład: Właściciel sklepu twierdzi, że 30% wszystkich jego weekendowych klientów przychodzi w piątek, 50% w sobotę i 20% w niedzielę. Niezależny badacz odwiedza sklep w losowy weekend i znajduje 91 klientów w piątek, 104 w sobotę i 65 w niedzielę. Stosując poziom istotności 0,10, wykonujemy test chi-kwadrat, aby sprawdzić dobroć dopasowania i określić, czy dane są zgodne z twierdzeniem właściciela sklepu.

W tym przypadku statystyka testowa wynosi 10 616.

Następnie możemy znaleźć krytyczną wartość testową w tabeli rozkładu Chi-kwadrat. Stopnie swobody są równe (#wyniki-1) = 3-1 = 2, a problem mówi nam, że powinniśmy zastosować poziom alfa równy 0,10. Zatem, zgodnie z tabelą rozkładu Chi-kwadrat, wartość krytyczna testu wynosi 4,605 .

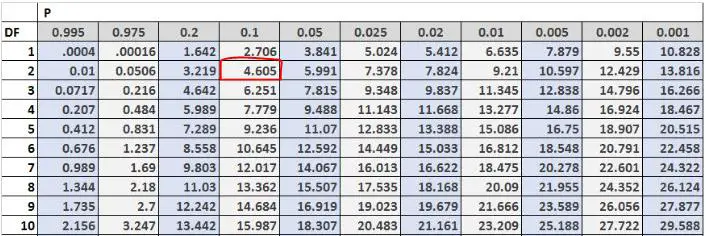
Ponieważ nasza statystyka testowa jest większa niż wartość krytyczna, odrzucamy hipotezę zerową. Oznacza to, że mamy wystarczające dowody, aby stwierdzić, że prawdziwy rozkład klientów przychodzących do tego sklepu w weekend nie jest równy 30% w piątek, 50% w sobotę i 20% w niedzielę.

Test chi-kwadrat na jednorodność

Testu chi-kwadrat sprawdzamy jednorodność , gdy chcemy formalnie sprawdzić, czy istnieje różnica w proporcjach między wieloma grupami.

Przykład: Ośrodek szkoleniowy koszykówki chce sprawdzić, czy dwa nowe programy szkoleniowe poprawią odsetek jego zawodników, którzy przejdą trudny test strzelecki. 172 graczy jest losowo przydzielonych do programu 1, 173 do programu 2, a 215 do bieżącego programu. Po miesiącu korzystania z programów treningowych zawodnicy przystępują następnie do egzaminu strzeleckiego. Poniższa tabela przedstawia liczbę zawodników, którzy przeszli test strzelecki, w zależności od używanego programu.

Stosując poziom istotności 0,05, przeprowadzamy test chi-kwadrat, aby określić, czy wskaźnik powodzenia jest taki sam dla każdego programu szkoleniowego.

Okazuje się, że statystyka testowa dla tego testu Chi-kwadrat wynosi 4,208.

Następnie możemy znaleźć krytyczną wartość testową w tabeli rozkładu Chi-kwadrat. Stopnie swobody są równe (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2, a problem powiedział nam, że powinniśmy zastosować poziom alfa równy 0,05. zgodnie z tabelą rozkładu chi-kwadrat wartość krytyczna testu wynosi 5,991 .

Ponieważ nasza statystyka testowa jest mniejsza niż wartość krytyczna, nie możemy odrzucić hipotezy zerowej. Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że te trzy programy szkoleniowe dają różne rezultaty.