Socs: przydatny akronim do opisu dystrybucji

W statystyce często chcemy zrozumieć, w jaki sposób zestaw danych jest dystrybuowany. W szczególności warto wiedzieć cztery rzeczy na temat dystrybucji:

1 . Kształt

• Czy rozkład jest symetryczny czy przechylony w jedną stronę?
• Czy rozkład jest unimodalny (jeden pik) czy bimodalny (dwa piki)?

2. Wartości odstające

• Czy w rozkładzie występują wartości odstające?

3. Centrum

• Jaka jest średnia, mediana i sposób dystrybucji?

4.Rozprzestrzenianie się

• Jaki jest rozstęp, rozstęp międzykwartylowy, odchylenie standardowe i wariancja rozkładu?

SOCS to przydatny akronim, którego możemy użyć, aby zapamiętać te cztery rzeczy. Oznacza „kształt, wartości odstające, środek, rozpiętość”.

Przeanalizujmy prosty przykład użycia SOCS do opisu dystrybucji.

Przykład: Jak używać SOCS do opisu dystrybucji

Załóżmy, że mamy następujący zestaw danych, który pokazuje wysokość próbki 20 różnych roślin.

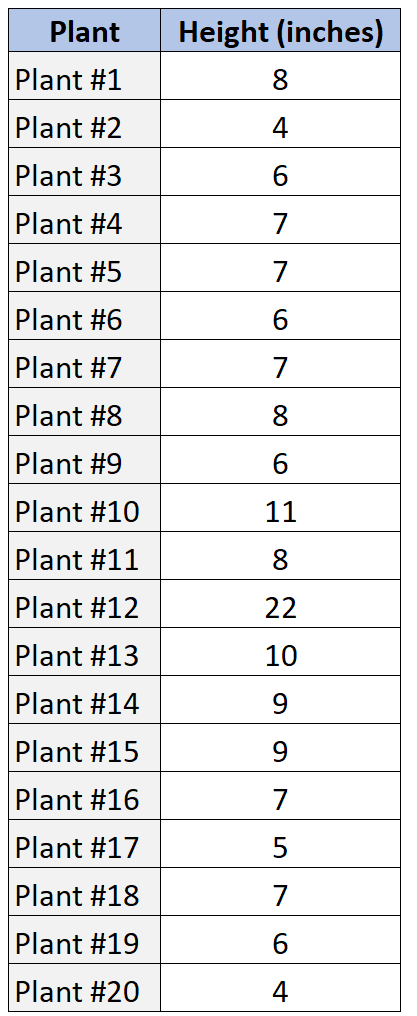
Oto, jak możemy użyć SOCS do opisania tego rozkładu wartości danych.

Kształt

Najpierw chcemy opisać kształt rozkładu.

Przydatnym sposobem wizualizacji kształtu rozkładu jest utworzenie histogramu przedstawiającego częstości występowania każdej wartości w zbiorze danych:

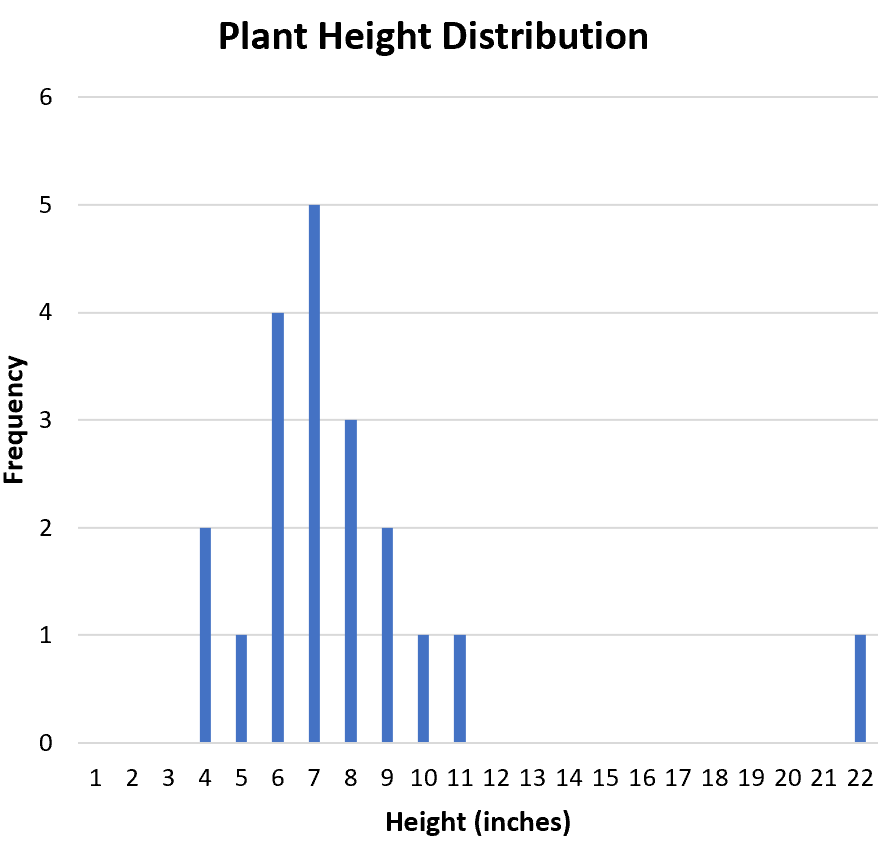
Czy rozkład jest symetryczny czy przechylony w jedną stronę?   Z histogramu widać, że rozkład jest w przybliżeniu symetryczny. Innymi słowy, wartości nie są stronnicze w ten czy inny sposób.

Czy rozkład jest unimodalny (jeden pik) czy bimodalny (dwa piki)? Dystrybucja jest jednomodalna. Ma szczyt przy wartości „7”.

Wartości odstające

Następnie chcemy sprawdzić, czy w zbiorze danych znajdują się wartości odstające. Na histogramie możemy wizualnie sprawdzić rozkład i zobaczyć, że 22 jest potencjalnie wartością odstającą:

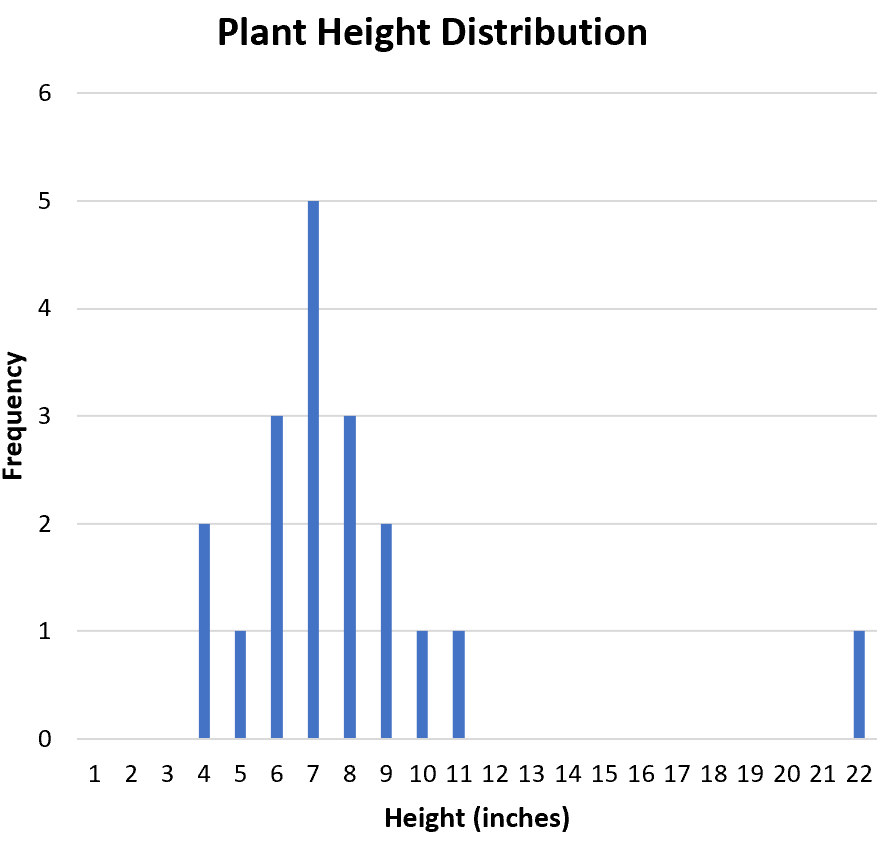
Typowym sposobem formalnego zdefiniowania wartości odstającej jest dowolna wartość stanowiąca 1,5-krotność zakresu międzykwartylowego powyżej trzeciego kwartyla lub poniżej pierwszego kwartyla.

Korzystając z kalkulatora rozstępu międzykwartylowego, możemy wprowadzić 20 wartości danych surowych i zobaczyć, że trzeci kwartyl wynosi 9 , rozstęp międzykwartylowy wynosi 3 , a zatem każda wartość większa niż 9 + (1,5*3) = 13,5 jest wartością odstającą, z definicji.

Ponieważ 22 jest większe niż 13,5, możemy uznać 22 za wartość odstającą.

Centrum

Następnie chcemy opisać, gdzie znajduje się centrum dystrybucji. Trzy popularne miary tendencji centralnej , których możemy użyć, to średnia, mediana i moda.

Średnia: Jest to średnia wartość rozkładu. Znajdujemy to, dodając wszystkie poszczególne wartości, a następnie dzieląc przez całkowitą liczbę wartości:

Średnia = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85

Mediana: Jest to „średnia” wartość rozkładu. Znajdujemy to, porządkując wszystkie wartości od najmniejszej do największej, a następnie identyfikując wartość mediany. Okazuje się, że 7 .

4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

Tryb: Jest to wartość, która pojawia się najczęściej. Okazuje się, że 7 .

Rozpowszechnianie się

Następnie chcemy opisać rozkład wartości w rozkładzie. Cztery popularne miary rozproszenia, których możemy użyć, to rozstęp, rozstęp międzykwarylowy, odchylenie standardowe i wariancja.

Zakres: Jest to różnica między największą i najmniejszą wartością w zbiorze danych. Okazuje się, że jest to 22 – 4 = 18 .

Rozstęp międzykwartylowy: Mierzy szerokość środkowych 50% wartości danych. Wprowadzając 20 surowych wartości danych do kalkulatora rozstępu międzykwartylowego, widzimy, że jest to równe 3 .

Odchylenie standardowe: Jest to miara średniego rozkładu wartości danych. Wpisując 20 wartości danych surowych do kalkulatora wariancji i odchylenia standardowego, widzimy, że odchylenie standardowe wynosi 3,69 .

Wariancja: Jest to po prostu odchylenie standardowe do kwadratu. Jest to równe 3,69 ² = 13,63 .

Wniosek

Korzystając ze wskazówek SOCS , mogliśmy opisać rozkład wysokości roślin w następujący sposób:

• Rozkład był jednomodalny i symetryczny, co oznacza, że miał tylko jeden pik i nie był przekrzywiony w żadną stronę.
• Rozkład miał jedną wartość odstającą: 22.
• Rozkład miał średnią 7,85, medianę 7 i modę 7.
• Rozkład miał zakres 18, rozstęp międzykwartylowy 3, odchylenie standardowe 3,69 i wariancję 13,63.

Zauważ, że możemy użyć SOCS do opisania dowolnego rozkładu, co jest dla nas przydatnym sposobem, aby w pełni zrozumieć kształt rozkładu, czy ma wartości odstające, gdzie w przybliżeniu znajduje się środek i jak rozłożyć wartości Dane. Czy.