Jak wykonać test t dla jednej próby w programie excel

Test t dla jednej próby służy do sprawdzenia, czy średnia populacji jest równa określonej wartości.

W tym samouczku wyjaśniono, jak wykonać test t dla jednej próby w programie Excel.

Jak wykonać test t dla jednej próby w programie Excel

Załóżmy, że botanik chce wiedzieć, czy średnia wysokość określonego gatunku rośliny wynosi 15 cali. Bierze losową próbkę 12 roślin i zapisuje wysokość każdej z nich w calach.

Poniższy obrazek przedstawia wysokość (w calach) każdej rośliny w próbce:

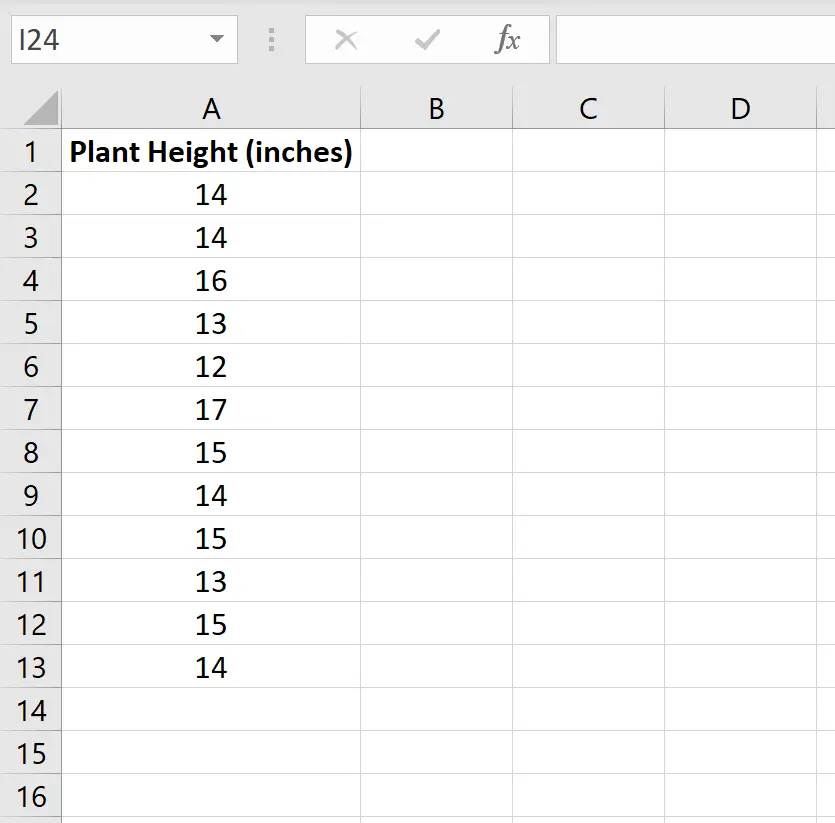
Możemy wykonać następujące kroki, aby przeprowadzić test t dla jednej próbki, aby ustalić, czy średnia wysokość tego gatunku rośliny wynosi w rzeczywistości 15 cali.

Krok 1: Znajdź wielkość próby, średnią próbkę i odchylenie standardowe próbki.

Najpierw musimy znaleźć wielkość próby, średnią próbki i odchylenie standardowe próbki, a wszystkie te czynniki zostaną wykorzystane do przeprowadzenia testu t dla jednej próby.

Poniższy obrazek przedstawia formuły, których możemy użyć do obliczenia tych wartości:

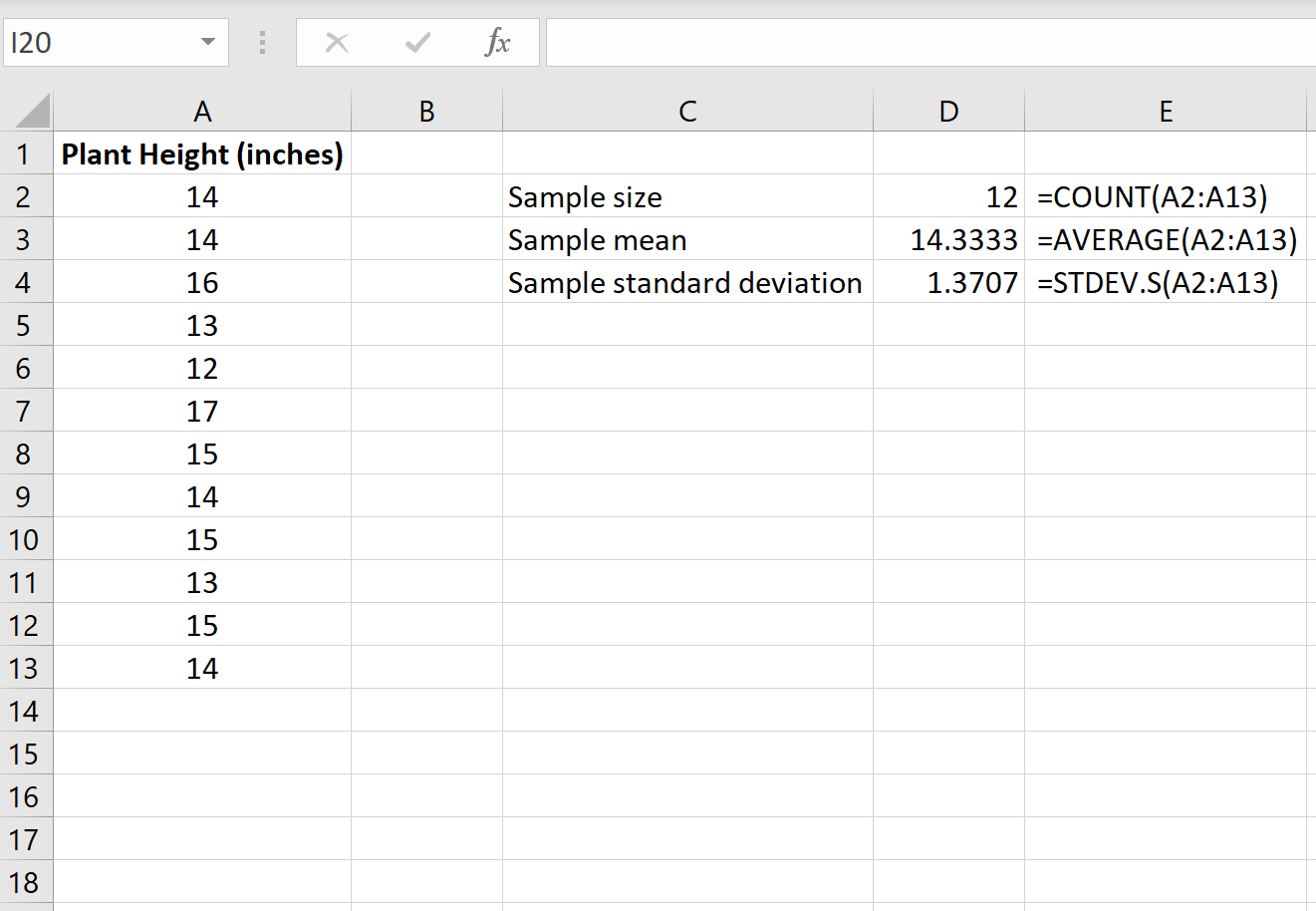
Krok 2: Oblicz statystykę testu t .

Następnie obliczymy statystykę testu t , korzystając z następującego wzoru:

t = x – µ / (s/ √n )

Złoto:

x = średnia próbki

µ = hipotetyczna średnia populacji

s = odchylenie standardowe próbki

n = wielkość próbki

Poniższy obrazek pokazuje, jak obliczyć t w programie Excel:

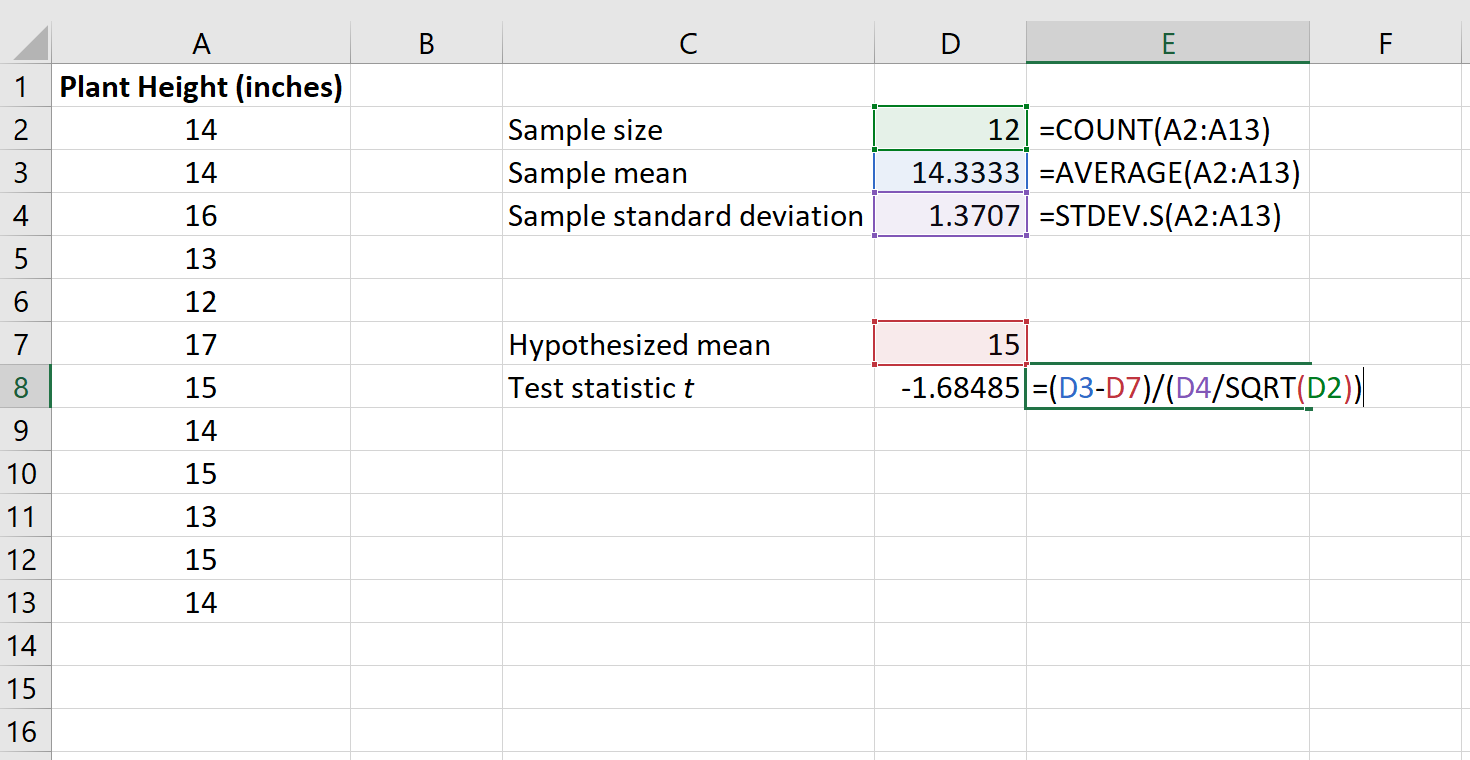
Statystyka testu t wynosi -1,68485 .

Krok 3: Oblicz wartość p statystyki testowej.

Następnie musimy obliczyć wartość p związaną ze statystyką testową, korzystając z następującej funkcji w programie Excel:

=T.ROZKŁ.2T(ABS(x), stopień_swobody)

Złoto:

x = t statystyka testowa

deg_freedom = stopnie swobody dla testu, obliczone jako n-1

Uwagi techniczne:

Funkcja T.DIST.2T() zwraca wartość p dla dwustronnego testu t. Jeśli zamiast tego wykonujesz test t dla lewej lub prawej strony, zamiast tego użyjesz odpowiednio funkcji T.DIST() lub T.DIST.RT() .

Poniższy obraz pokazuje, jak obliczyć wartość p dla naszej statystyki testowej:

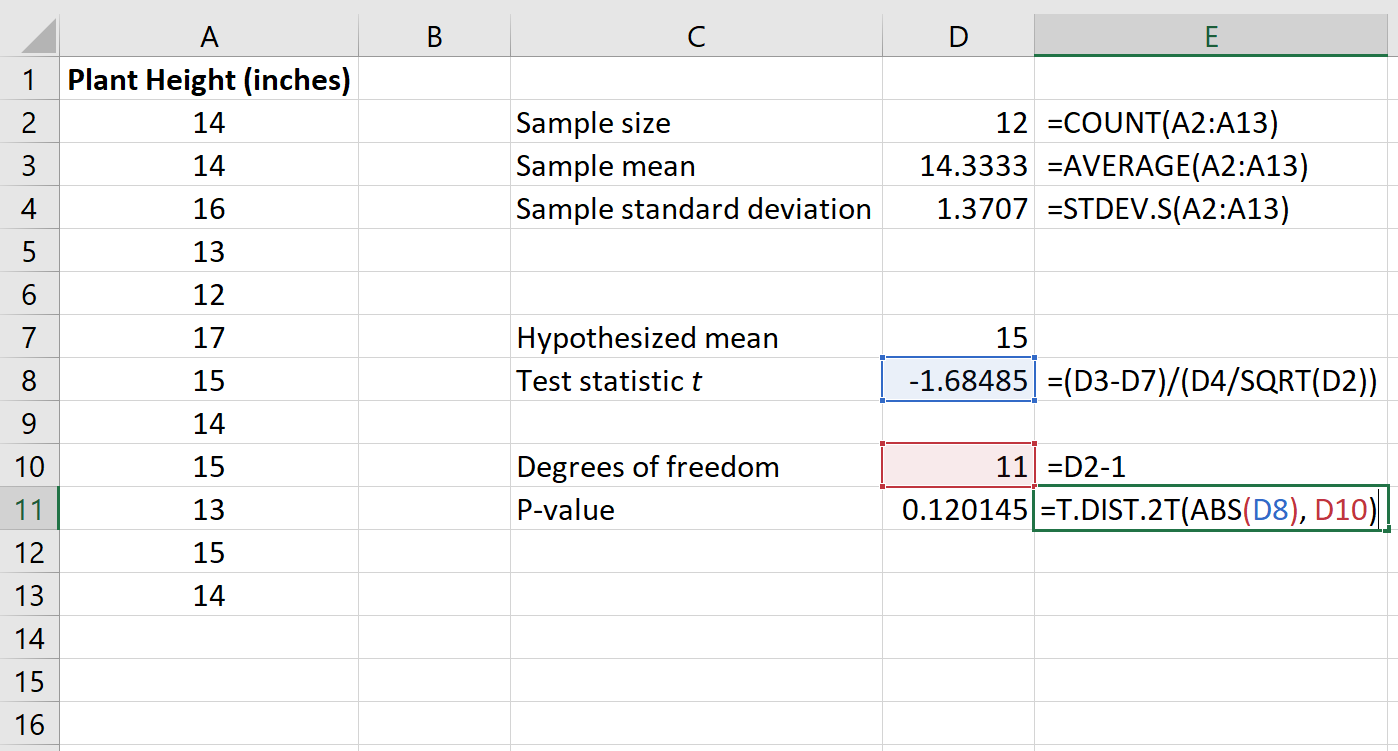
Wartość p wynosi 0,120145 .

Krok 4: Interpretacja wyników.

Dwie hipotezy dotyczące tego testu t na konkretnej próbie są następujące:

H ₀ : µ = 15 (średnia wysokość tego gatunku rośliny wynosi 15 cali)

H _A : µ ≠15 (średnia wysokość nie wynosi 15 cali)

Wartość p naszego testu (0,120145) jest większa niż alfa = 0,05, więc nie możemy odrzucić hipotezy zerowej testu.

Nie mamy wystarczających dowodów, aby stwierdzić, że średnia wysokość tego konkretnego gatunku rośliny jest inna niż 15 cali.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne popularne typy testów t w programie Excel:

Jak wykonać test t dla dwóch próbek w programie Excel
Jak wykonać test t dla par próbek w programie Excel