Tau kendalla: definicja + przykład

W statystyce korelacja odnosi się do siły i kierunku związku między dwiema zmiennymi. Wartość współczynnika korelacji może mieścić się w zakresie od -1 do 1, gdzie -1 oznacza idealną ujemną zależność, 0 oznacza brak związku, a 1 oznacza doskonałą dodatnią zależność.

Najczęściej stosowanym współczynnikiem korelacji jest współczynnik korelacji Pearsona , który mierzy liniowe powiązanie między dwiema zmiennymi numerycznymi.

Rzadziej stosowanym współczynnikiem korelacji jest Tau Kendalla , który mierzy związek między dwiema kolumnami danych rankingowych.

Wzór na obliczenie Tau Kendalla, często w skrócie τ, jest następujący:

τ = (CD) / (C+D)

Złoto:

C = liczba pasujących par

D = liczba niezgodnych par

Poniższy przykład ilustruje sposób użycia tej formuły do obliczenia współczynnika korelacji rang Tau Kendalla dla dwóch kolumn danych rankingowych.

Przykład obliczenia Tau Kendalla

Zakłada się, że dwóch trenerów koszykówki uszereguje 12 swoich zawodników od najgorszego do najlepszego. Poniższa tabela przedstawia rankingi przypisane zawodnikom przez każdego trenera:

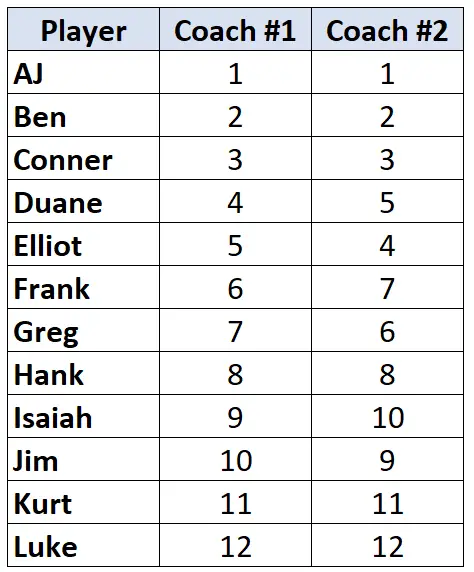
Ponieważ pracujemy z dwiema kolumnami danych rankingowych, właściwe jest użycie Tau Kendalla do obliczenia korelacji pomiędzy rankingami dwóch trenerów. Aby obliczyć Tau Kendalla, wykonaj następujące kroki:

Krok 1: Policz liczbę pasujących par.

Spójrz tylko na rankingi trenera nr 2. Zaczynając od pierwszego gracza, policz, o ile rang pod nim jest wyższy . Na przykład poniżej „1” znajduje się 11 liczb, które są większe, więc napiszemy 11:

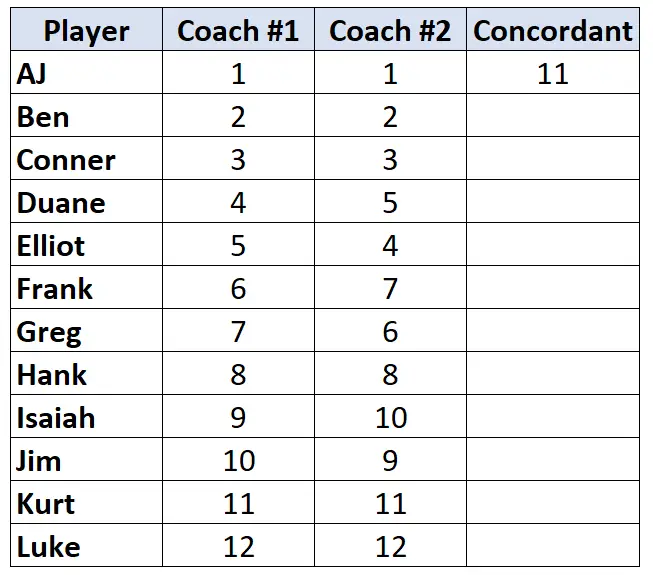
Przejdź do następnego gracza i powtórz proces. Poniżej „2” znajduje się 10 liczb, które są większe, więc napiszemy 10:

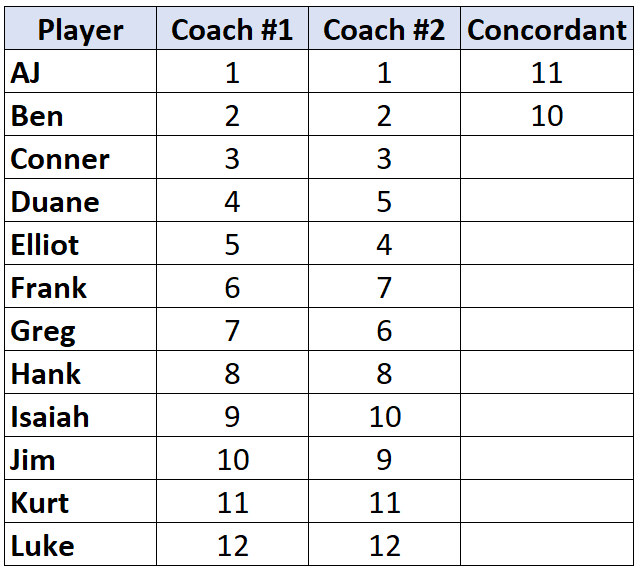
Gdy dotrzemy do gracza, którego ranga jest niższa niż gracz przed nim, po prostu zostaje mu przypisana ta sama wartość, co graczowi przed nim. Na przykład Elliot ma rangę „4”, która jest niższa niż ranga poprzedniego gracza wynosząca „5”, więc otrzymuje po prostu tę samą wartość, co gracz przed nim:

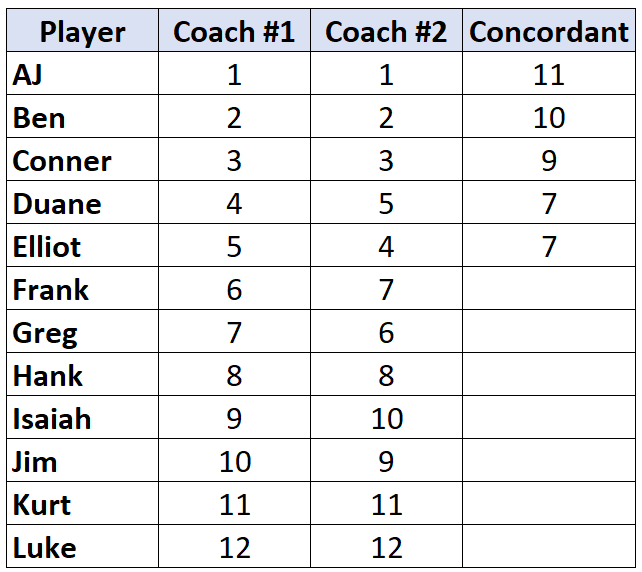
Powtórz ten proces dla wszystkich graczy:

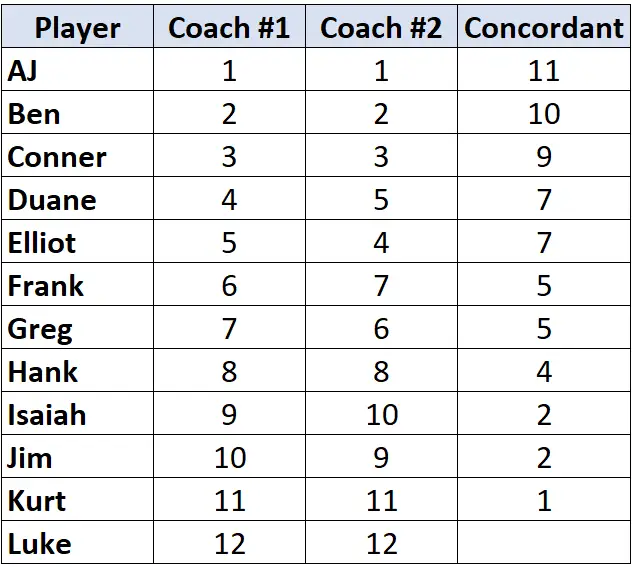
Krok 2: Policz liczbę niezgodnych par.

Ponownie spójrz tylko na rankingi trenera nr 2. Dla każdego gracza policz, o ile rang pod nim jest mniejszych . Na przykład trener nr 2 przypisał AJ-owi rangę „1” i żaden zawodnik pod nim nie ma niższej rangi. Dlatego przypisujemy mu wartość 0:

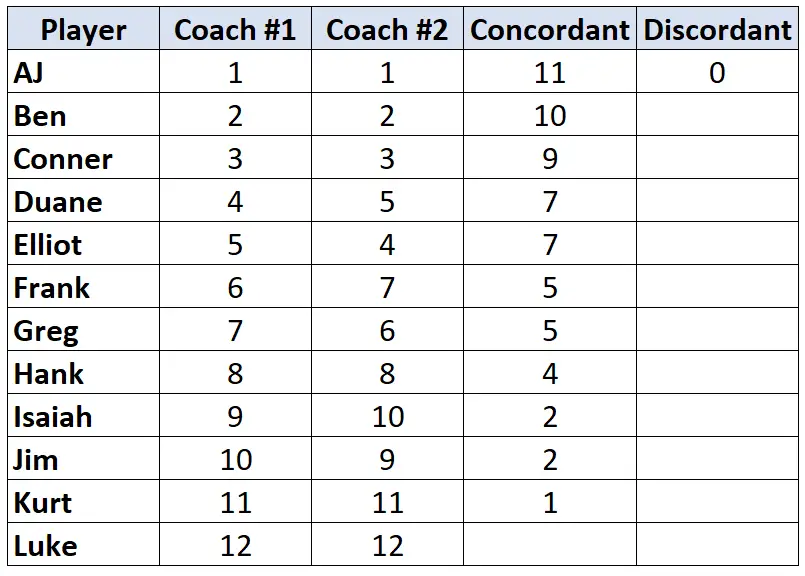
Powtórz ten proces dla każdego gracza:

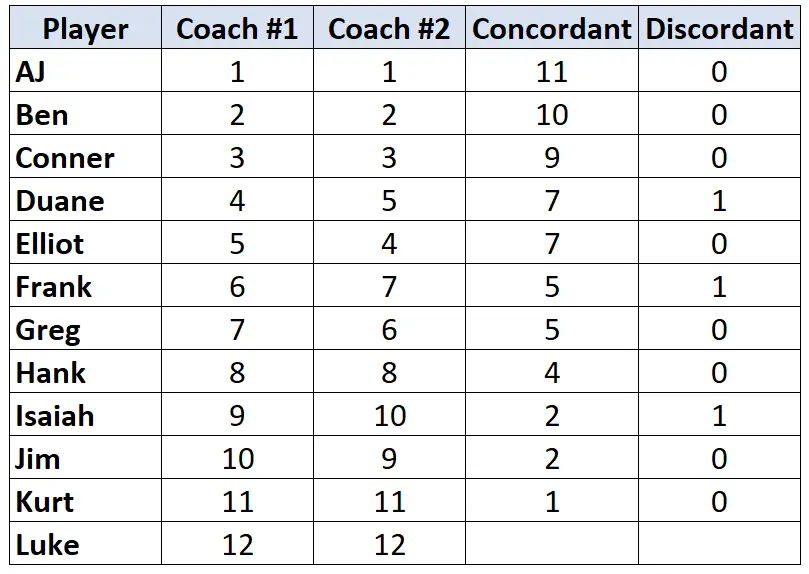
Krok 3: Oblicz sumę w każdej kolumnie i znajdź Tau Kendalla.

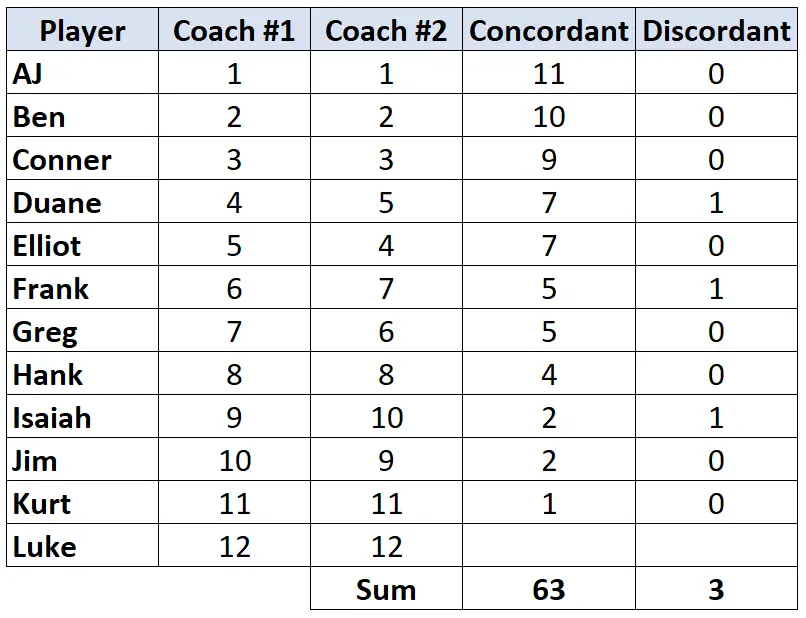
Tau Kendalla = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0,909 .

Statystyczne znaczenie Tau Kendalla

Jeśli masz więcej niż n=10 par, Tau Kendalla na ogół ma rozkład normalny. Do obliczenia współczynnika Z dla Tau Kendalla można użyć poniższego wzoru:

z = 3τ*√ n(n-1) / √ 2(2n+5)

Złoto:

τ = wartość obliczona dla Tau Kendalla

n = liczba par

Oto jak obliczyć z w poprzednim przykładzie:

z = 3(0,909)*√ 12(12-1) / √ 2(2*12+5) = 4,11 .

Korzystając z kalkulatora wartości P Z-score, widzimy, że wartość p dla tego wyniku Z wynosi 0,00004 , co jest statystycznie istotne na poziomie alfa 0,05. Istnieje zatem istotna statystycznie korelacja pomiędzy rangami, jakie obaj trenerzy przydzielili zawodnikom.

Bonus: Jak obliczyć Tau Kendalla w R

W oprogramowaniu statystycznym R można użyć funkcji kendall.tau() z biblioteki VGAM do obliczenia Tau Kendalla dla dwóch wektorów, stosując następującą składnię:

kendall.tau(x, y)

gdzie x i y to dwa wektory cyfrowe o równej długości.

Poniższy kod ilustruje sposób obliczenia Tau Kendalla dla dokładnych danych, których użyliśmy w poprzednim przykładzie:

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

Zwróć uwagę, jak wartość Tau Kendalla odpowiada wartości obliczonej ręcznie.