Jak wykonać test t dla sparowanych próbek w stata
Test t dla par prób służy do porównania średnich z dwóch próbek, gdy każdą obserwację w jednej próbie można powiązać z obserwacją w drugiej próbie.
W tym samouczku wyjaśniono, jak wykonać test t dla par próbek w Stata.
Przykład: Test t dla par prób w Stata
Naukowcy chcą wiedzieć, czy nowy sposób uzdatniania paliwa powoduje zmianę średniego zużycia paliwa przez określony samochód. Aby to sprawdzić, przeprowadzają eksperyment, w którym mierzą mpg 12 samochodów z uzdatnieniem paliwa i bez niego.
Ponieważ każdy samochód jest poddawany zabiegowi, możemy przeprowadzić test t dla par, w którym każdy samochód jest powiązany ze sobą, aby określić, czy istnieje różnica w średnim przebiegu na trasie z uzdatnieniem paliwa i bez niego.
Wykonaj poniższe kroki, aby wykonać test t dla par w Stata.
Krok 1: Załaduj dane.
Najpierw załaduj dane, wpisując use https://www.stata-press.com/data/r13/fuel w polu poleceń i klikając Enter.
Krok 2: Wyświetl surowe dane.
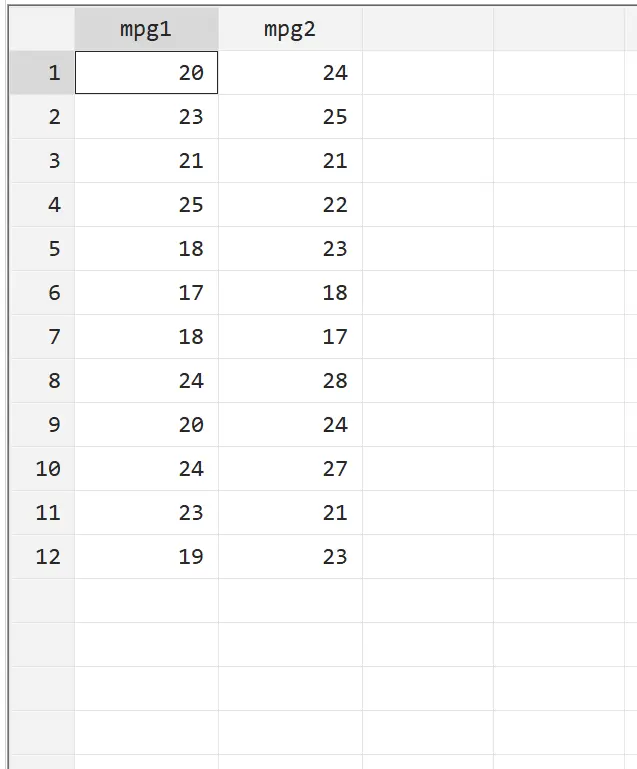
Przed wykonaniem testu t dla par przyjrzyjmy się najpierw surowym danym. Z górnego paska menu przejdź do opcji Dane > Edytor danych > Edytor danych (Przeglądaj) . Pierwsza kolumna, mpg1 , wyświetla mpg pierwszego samochodu bez uzdatniania paliwa, podczas gdy druga kolumna, mpg2 , wyświetla mpg pierwszego samochodu z uzdatnieniem paliwa.
Krok 3: Wykonaj test t dla par.
Z górnego paska menu wybierz Statystyka > Podsumowania, tabele i testy > Klasyczne testy hipotez > Test t (test porównania średnich) .
Wybierz opcję Sparowane. Jako Pierwsza zmienna wybierz mpg1 . Jako Druga zmienna wybierz mpg2 . W obszarze Poziom zaufania wybierz żądany poziom. Wartość 95 odpowiada poziomowi istotności 0,05. Zostawmy to na 95. Na koniec kliknij OK .
Wyświetlone zostaną sparowane wyniki testu t:
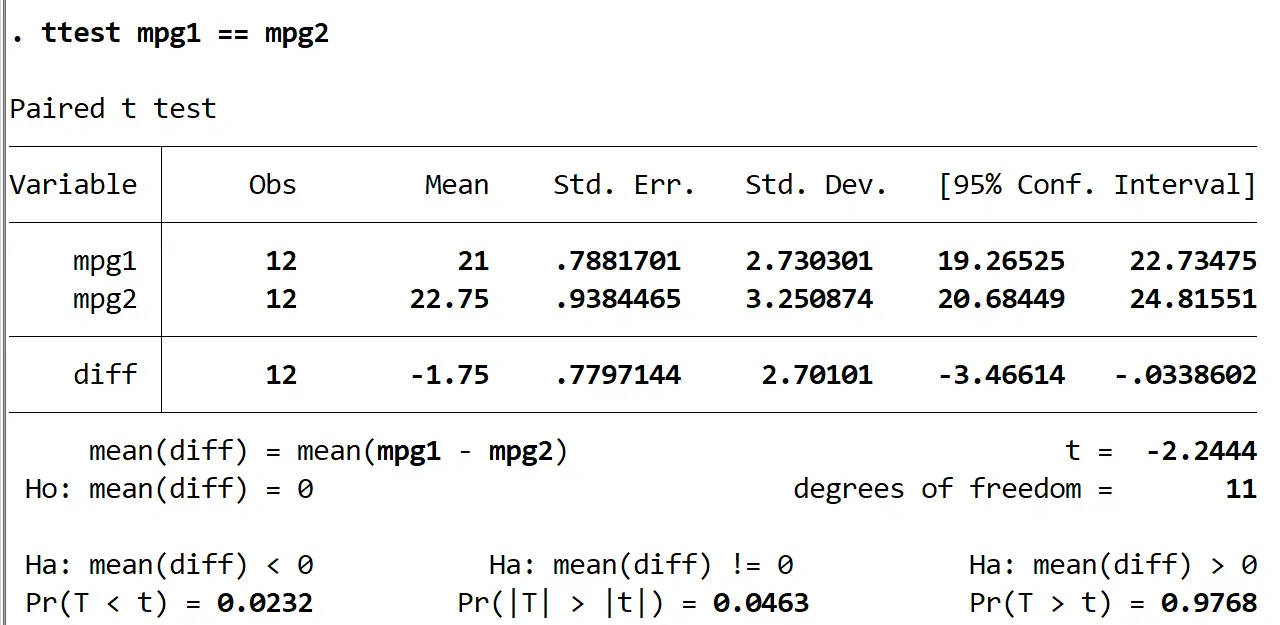
Dla każdej grupy otrzymujemy następujące informacje:
Obs: Liczba obserwacji. W każdej grupie jest 12 obserwacji.
Średnia: średnia mpg. W grupie 0 średnia wynosi 21. W grupie 1 średnia wynosi 22,75.
Standard. Err: błąd standardowy obliczony jako σ / √ n
Standard. Dev: odchylenie standardowe mpg.
95% konf. Zakres: 95% przedział ufności dla prawdziwej średniej populacji w mpg.
t: statystyka testowa testu t dla par.
stopnie swobody: stopnie swobody stosowane w badaniu, obliczane w następujący sposób: #pairs-1 = 12-1 = 11.
Wartości p dla trzech różnych testów t dla dwóch próbek pokazano na dole wyników. Ponieważ chcemy zrozumieć, czy średnie mpg po prostu różni się w obu grupach, przyjrzymy się wynikom testu pośredniego (w którym alternatywną hipotezą jest Ha:diff !=0), którego wartość p wynosi 0,0463. .
Ponieważ wartość ta jest poniżej naszego poziomu istotności 0,05, odrzucamy hipotezę zerową. Mamy wystarczająco dużo dowodów, aby stwierdzić, że rzeczywista średnia wartość mpg różni się w obu grupach.
Krok 5: Ogłoś wyniki.
Na koniec podamy wyniki naszego testu t dla par. Oto przykład, jak to zrobić:
Przeprowadzono test t dla 12 samochodów w celu ustalenia, czy nowe uzdatnienie paliwa spowodowało różnicę w średnim przebiegu na galonie.
Wyniki pokazały, że średnie mpg było statystycznie istotne różniły się pomiędzy obiema grupami (t = -2,2444 przy df=11, p = 0,0463) na poziomie istotności 0,05.
95% przedział ufności dla prawdziwej różnicy między średnimi z populacji dał przedział (-3,466; -0,034).
Na podstawie tych wyników nowe uzdatnianie paliwa prowadzi do statystycznie znacząco wyższych mpg dla samochodów osobowych.