Jak wykonać prostą regresję liniową w stata

Prosta regresja liniowa to metoda, której można użyć do zrozumienia związku między zmienną objaśniającą x i zmienną odpowiedzi y.

W tym samouczku wyjaśniono, jak wykonać prostą regresję liniową w programie Stata.

Przykład: Prosta regresja liniowa w Stata

Załóżmy, że chcemy zrozumieć związek pomiędzy masą samochodu a liczbą mil na galon. Aby zbadać tę zależność, możemy przeprowadzić prostą regresję liniową, używając masy jako zmiennej objaśniającej i mil na galon jako zmiennej odpowiedzi.

Wykonaj poniższe kroki w programie Stata, aby przeprowadzić prostą regresję liniową, korzystając ze zbioru danych o nazwie auto , który zawiera dane dotyczące 74 różnych samochodów.

Krok 1: Załaduj dane.

Załaduj dane, wpisując w polu poleceń:

użyj https://www.stata-press.com/data/r13/auto

Krok 2: Uzyskaj podsumowanie danych.

Aby szybko zrozumieć dane, z którymi pracujesz, wpisz następujące polecenie w polu Polecenie:

podsumować

Widzimy, że w zbiorze danych znajduje się 12 różnych zmiennych, ale interesują nas tylko dwie: mpg i waga .

Krok 3: Wizualizuj dane.

Przed wykonaniem prostej regresji liniowej utwórzmy najpierw wykres rozrzutu masy w funkcji mpg, abyśmy mogli zwizualizować związek między tymi dwiema zmiennymi i sprawdzić oczywiste wartości odstające. Wpisz następujące polecenie w polu polecenia, aby utworzyć wykres rozrzutu:

rozproszenie masy w mpg

Daje to następujący wykres punktowy:

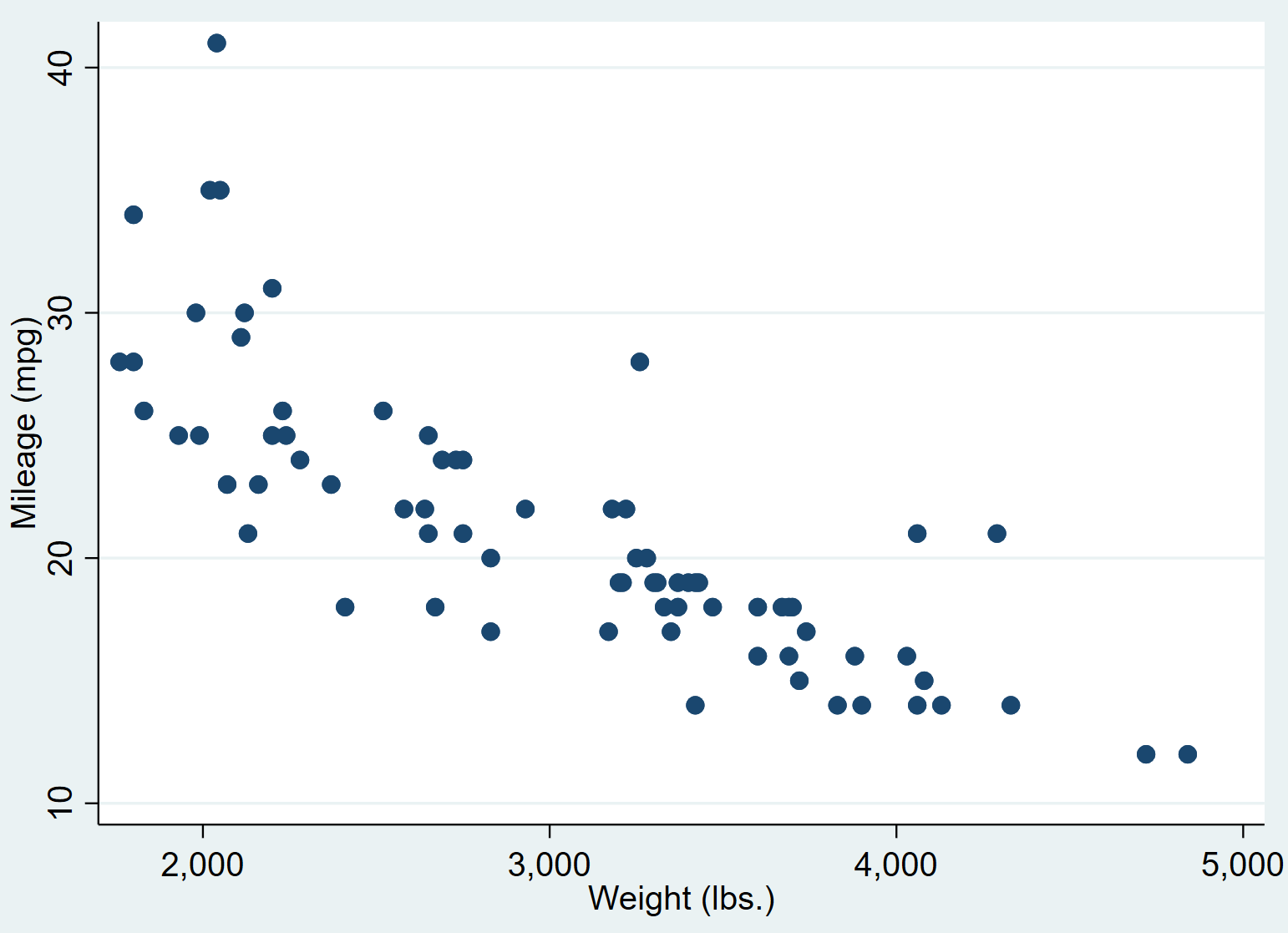
Widzimy, że samochody o większej masie mają zwykle mniej mil na galon. Aby określić ilościowo tę zależność, przeprowadzimy teraz prostą regresję liniową.

Krok 4: Wykonaj prostą regresję liniową.

Wpisz następujące polecenie w polu Polecenie, aby wykonać prostą regresję liniową, używając wagi jako zmiennej objaśniającej i mpg jako zmiennej odpowiedzi.

cofnij wagę do mpg

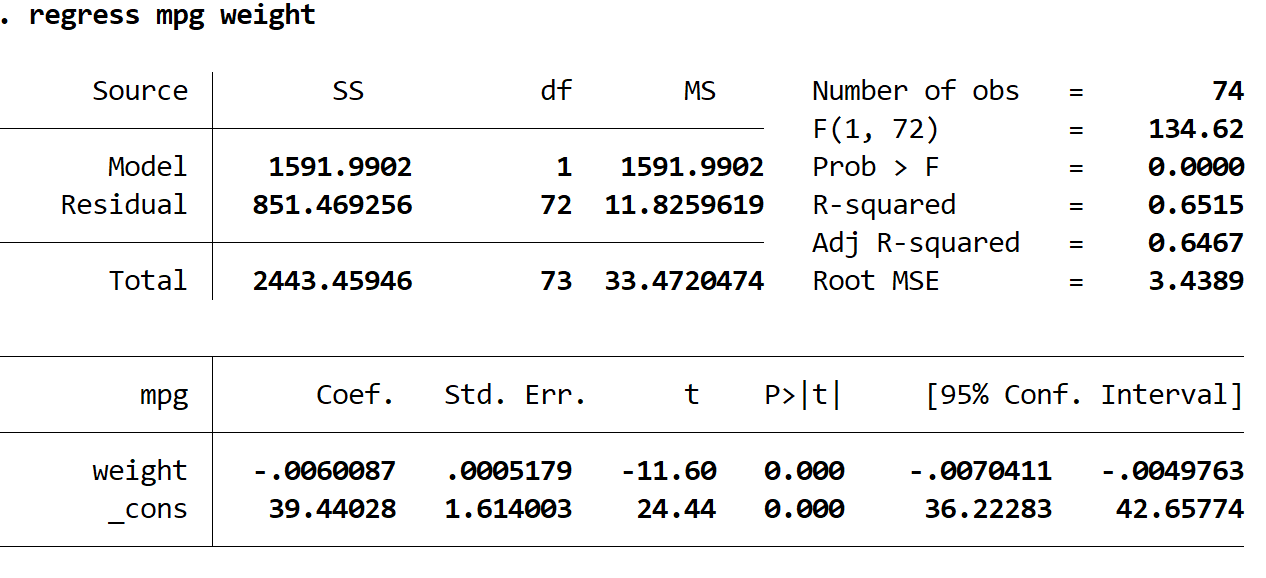
Oto jak zinterpretować najciekawsze liczby w wyniku:

R do kwadratu: 0,6515. Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennej objaśniającej. W tym przykładzie 65,15% zmiany w mpg można wyjaśnić wagą.

Współczynnik (waga): -0,006. To mówi nam o średniej zmianie zmiennej odpowiedzi powiązanej ze wzrostem o jedną jednostkę zmiennej objaśniającej. W tym przykładzie każdy funt wzrostu masy ciała wiąże się ze spadkiem masy ciała średnio o 0,006 mpg.

Współczynnik (_cons): 39,44028. Mówi nam to o średniej wartości zmiennej odpowiedzi, gdy zmienna objaśniająca wynosi zero. W tym przykładzie średnia mpg wynosi 39,44028, gdy masa samochodu wynosi zero. Interpretacja tego nie ma sensu, ponieważ masa samochodu nie może wynosić zero, ale liczba 39,44028 jest konieczna do utworzenia równania regresji.

P>|t| (waga): 0,000. Jest to wartość p powiązana ze statystyką testową dotyczącą masy ciała. W tym przypadku, ponieważ wartość ta jest mniejsza niż 0,05, możemy stwierdzić, że istnieje statystycznie istotna zależność pomiędzy masą a mpg.

Równanie regresji: Na koniec możemy utworzyć równanie regresji, korzystając z dwóch wartości współczynników. W tym przypadku równanie wyglądałoby następująco:

przewidywane mpg = 39,44028 – 0,0060087*(waga)

Możemy użyć tego równania, aby znaleźć oczekiwaną ilość mpg dla samochodu, biorąc pod uwagę jego masę. Na przykład samochód ważący 4000 funtów powinien mieć 15 405 mpg:

przewidywane mpg = 39,44028 – 0,0060087*(4000) = 15,405

Krok 5: Ogłoś wyniki.

Na koniec chcemy zgłosić wyniki naszej prostej regresji liniowej. Oto przykład, jak to zrobić:

Przeprowadzono regresję liniową, aby określić ilościowo związek między masą samochodu a liczbą mil na galon. Do analizy wykorzystano próbę 74 samochodów.

Wyniki wykazały, że istnieje statystycznie istotna zależność pomiędzy masą ciała a mpg (t = -11,60, p < 0,0001) i że waga stanowi 65,15% wyjaśnionej zmienności w mpg.

Równanie regresji okazało się następujące:

przewidywane mpg = 39,44 – 0,006 (waga)

Każdy dodatkowy funt wiązał się ze spadkiem średnio o -0,006 mili na galon.