Jak wykonać manova w stata

Jednoczynnikową analizę ANOVA stosuje się w celu ustalenia, czy różne poziomy zmiennej objaśniającej prowadzą do statystycznie różnych wyników w przypadku określonych zmiennych odpowiedzi.

Na przykład możemy być zainteresowani zrozumieniem, czy trzy poziomy wykształcenia (stopień nadzwyczajny, licencjat, tytuł magistra) prowadzą do statystycznie różnych rocznych zarobków. W tym przypadku mamy zmienną objaśniającą i zmienną odpowiedzi.

• Zmienna objaśniająca: poziom wykształcenia
• Zmienna odpowiedzi: roczny dochód

MANOVA jest rozszerzeniem jednokierunkowej ANOVA, w której występuje więcej niż jedna zmienna odpowiedzi. Na przykład możemy być zainteresowani zrozumieniem, czy poziom wykształcenia prowadzi do różnych rocznych dochodów i różnych kwot długów studenckich. W tym przypadku mamy jedną zmienną objaśniającą i dwie zmienne odpowiedzi:

• Zmienna objaśniająca: poziom wykształcenia
• Zmienne odpowiedzi: roczny dochód, zadłużenie studenckie

Ponieważ mamy więcej niż jedną zmienną odpowiedzi, w tym przypadku właściwe byłoby użycie MANOVA.

Następnie wyjaśnimy, jak wykonać MANOVA w Stata.

Przykład: MANOVA w Stata

Aby zilustrować, jak wykonać MANOVA w Stata, użyjemy następującego zbioru danych, który zawiera następujące trzy zmienne dla 24 osób:

• edu: poziom studiów (0 = Associate, 1 = Bachelor, 2 = Master)
• dochód: dochód roczny
• zadłużenie: całkowite zadłużenie z tytułu kredytów studenckich

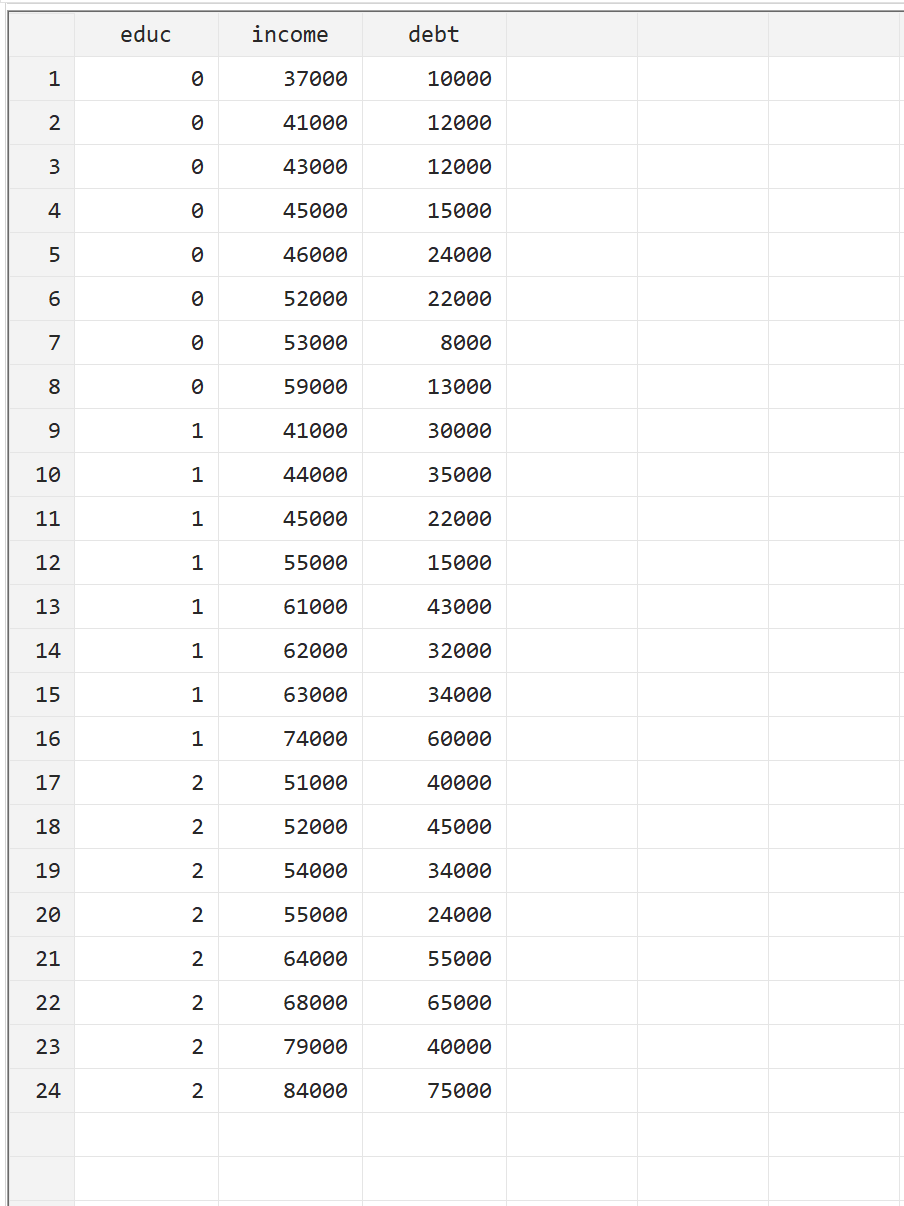
Możesz odtworzyć ten przykład, ręcznie wprowadzając dane, przechodząc do opcji Dane > Edytor danych > Edytor danych (Edytuj) na górnym pasku menu.

Aby wykonać MANOVA, używając wykształcenia jako zmiennej objaśniającej oraz dochodu i zadłużenia jako zmiennych odpowiedzi, możemy użyć następującego polecenia:

dochód, dług manova = edu

Stata generuje cztery unikalne statystyki testowe wraz z odpowiadającymi im wartościami p:

Lambda Wilksa: statystyka F = 5,02, wartość P = 0,0023.

Wykres Pillai: statystyka F = 4,07, wartość P = 0,0071.

Wykres Lawleya-Hotellinga: statystyka F = 5,94, wartość P = 0,0008.

Największy pierwiastek Roya: statystyka F = 13,10, wartość P = 0,0002.

Szczegółowe wyjaśnienie sposobu obliczania każdej statystyki testowej można znaleźć w tym artykule z Penn State Eberly College of Science.

Wartość p dla każdej statystyki testowej jest mniejsza niż 0,05, więc hipoteza zerowa zostanie odrzucona niezależnie od tego, której użyjesz. Oznacza to, że mamy wystarczające dowody, aby stwierdzić, że poziom wykształcenia powoduje statystycznie istotne różnice w rocznych dochodach i całkowitym zadłużeniu studentów.

Uwaga dotycząca wartości p: Litera obok wartości p w tabeli wyjściowej wskazuje, w jaki sposób obliczono statystykę F (e = obliczenie dokładne, a = obliczenie przybliżone, u = górna granica).