Jak przetestować wieloliniowość w stata

Wielokolinearność w analizie regresji ma miejsce, gdy dwie lub więcej zmiennych objaśniających jest ze sobą silnie skorelowanych, w związku z czym nie dostarczają unikalnych lub niezależnych informacji w modelu regresji. Jeśli stopień korelacji między zmiennymi jest wystarczająco wysoki, może to powodować problemy podczas dopasowywania i interpretacji modelu regresji.

Załóżmy na przykład, że przeprowadzasz wielokrotną regresję liniową z następującymi zmiennymi:

Zmienna reakcja: maksymalny skok w pionie

Zmienne objaśniające: rozmiar buta, wzrost, czas spędzony na ćwiczeniach

W tym przypadku zmienne objaśniające rozmiar i wysokość buta są prawdopodobnie silnie skorelowane, ponieważ wysocy ludzie mają zwykle większe rozmiary butów. Oznacza to, że wieloliniowość prawdopodobnie będzie problemem w tej regresji.

Na szczęście możliwe jest wykrycie wieloliniowości za pomocą metryki zwanej współczynnikiem inflacji wariancji (VIF) , która mierzy korelację i siłę korelacji pomiędzy zmiennymi objaśniającymi w modelu regresji.

W tym samouczku wyjaśniono, jak używać VIF do wykrywania współliniowości w analizie regresji w Stata.

Przykład: wieloliniowość w Stata

W tym przykładzie użyjemy wbudowanego zbioru danych Staty o nazwie auto . Użyj następującego polecenia, aby załadować zestaw danych:

używać automatycznie

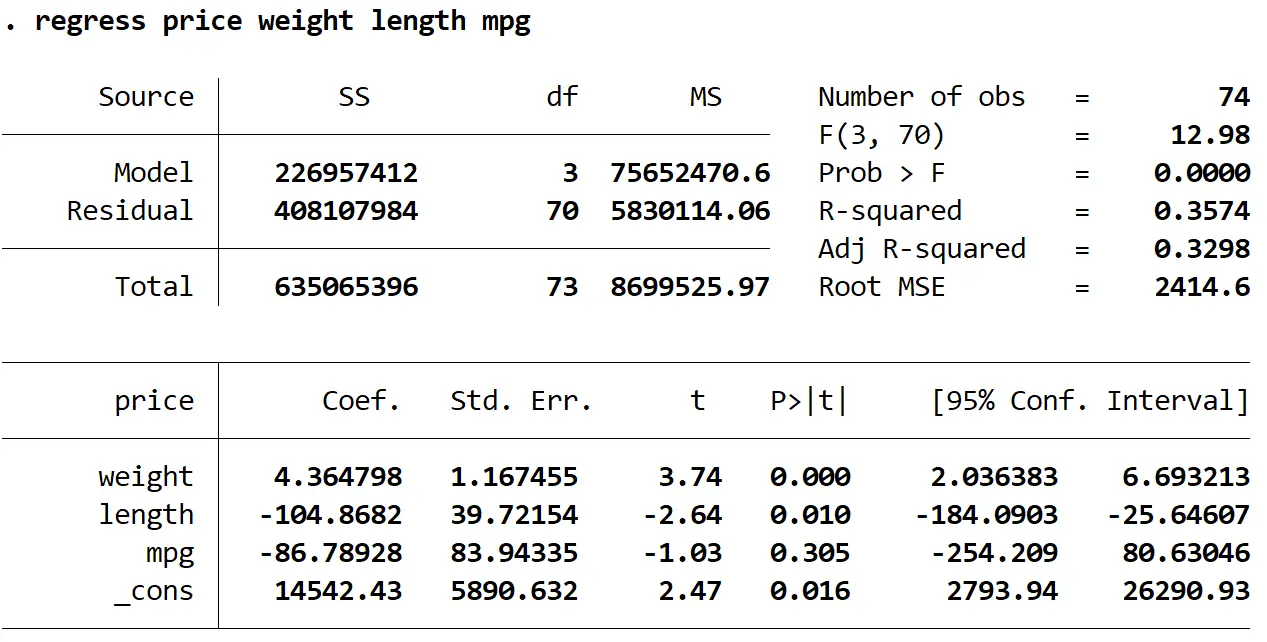
Użyjemy polecenia regress , aby dopasować model regresji liniowej wielokrotnej, używając ceny jako zmiennej odpowiedzi oraz wagi, długości i mpg jako zmiennych objaśniających:

regresja cena waga długość mpg

Następnie użyjemy polecenia vive do przetestowania wielowspółliniowości:

pełen życia

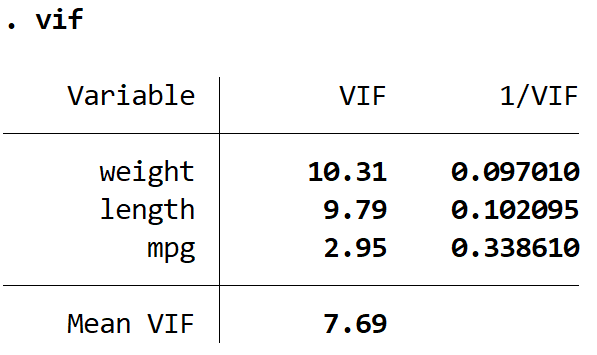
Daje to wartość VIF dla każdej zmiennej objaśniającej w modelu. Wartość VIF zaczyna się od 1 i nie ma górnej granicy. Ogólna zasada interpretacji VIF jest następująca:

• Wartość 1 oznacza, że pomiędzy daną zmienną objaśniającą a jakąkolwiek inną zmienną objaśniającą w modelu nie ma korelacji.
• Wartość od 1 do 5 wskazuje na umiarkowaną korelację pomiędzy daną zmienną objaśniającą a innymi zmiennymi objaśniającymi w modelu, jednak często nie jest ona na tyle poważna, aby wymagała szczególnej uwagi.
• Wartość większa od 5 wskazuje na potencjalnie silną korelację pomiędzy daną zmienną objaśniającą a innymi zmiennymi objaśniającymi w modelu. W tym przypadku szacunki współczynników i wartości p w wynikach regresji są prawdopodobnie niewiarygodne.

Widzimy, że wartości VIF dla masy i długości są większe niż 5, co wskazuje, że wieloliniowość jest prawdopodobnie problemem w modelu regresji.

Jak sobie radzić z wielowspółliniowością

Często najłatwiejszym sposobem poradzenia sobie z wielowspółliniowością jest po prostu usunięcie jednej ze zmiennych problematycznych, ponieważ usuwana zmienna i tak jest prawdopodobnie zbędna i dodaje do modelu niewiele unikalnych lub niezależnych informacji.

Aby określić, którą zmienną należy usunąć, możemy użyć polecenia corr w celu utworzenia macierzy korelacji wyświetlającej współczynniki korelacji pomiędzy każdą zmienną w modelu, co może pomóc nam zidentyfikować, które zmienne mogą być ze sobą silnie skorelowane i mogą powodować problem wielowspółliniowości:

corr cena waga długość mpg

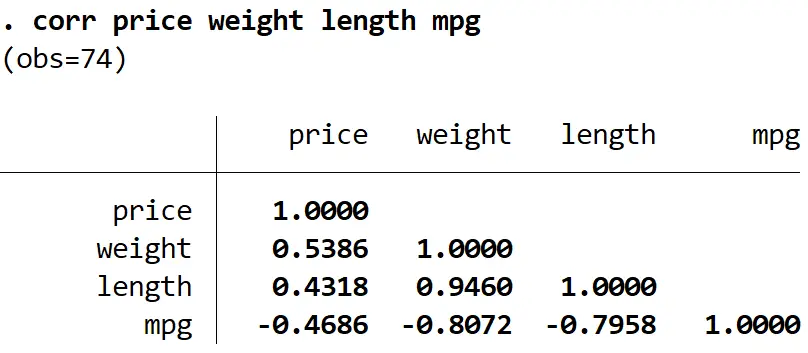
Widzimy, że długość jest silnie skorelowana zarówno z masą, jak i mpg, a najniższą korelację ma ze zmienną ceną odpowiedzi. Zatem usunięcie długości modelu mogłoby rozwiązać problem współliniowości bez pogarszania ogólnej jakości modelu regresji.

Aby to przetestować, możemy ponownie przeprowadzić analizę regresji, używając wyłącznie masy i mpg jako zmiennych objaśniających:

regresja cena waga mpg

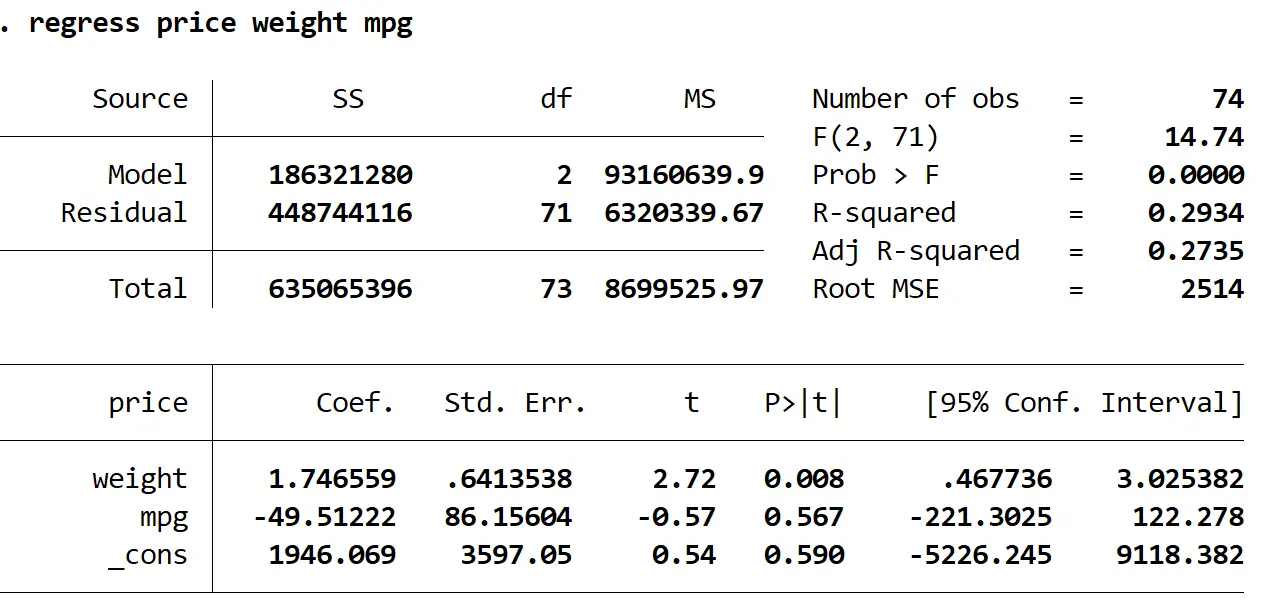
Widzimy, że skorygowany R-kwadrat tego modelu wynosi 0,2735 w porównaniu do 0,3298 w poprzednim modelu. Oznacza to, że ogólna użyteczność modelu tylko nieznacznie spadła. Następnie możemy znaleźć wartości VIF za pomocą polecenia VIF :

PEŁEN ŻYCIA

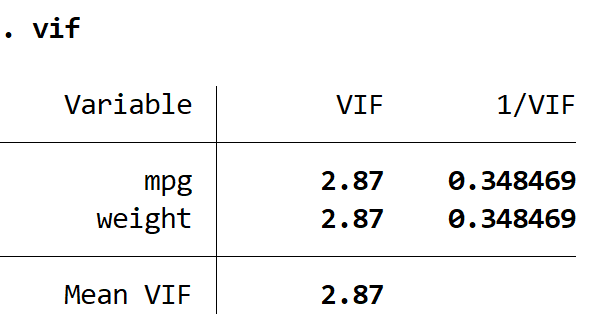
Obie wartości VIF są mniejsze niż 5, co wskazuje, że wieloliniowość nie jest już problemem w modelu.