Jak wykonać wielokrotną regresję liniową w programie excel
Wielokrotna regresja liniowa to metoda, którą możemy wykorzystać do zrozumienia związku między dwiema lub większą liczbą zmiennych objaśniających azmienną odpowiedzi .
W tym samouczku wyjaśniono, jak przeprowadzić wielokrotną regresję liniową w programie Excel.
Uwaga: jeśli masz tylko jedną zmienną objaśniającą, powinieneś zamiast tego przeprowadzić prostą regresję liniową .
Przykład: Wielokrotna regresja liniowa w programie Excel
Załóżmy, że chcemy wiedzieć, czy liczba godzin spędzonych na nauce i liczba zdanych egzaminów przygotowawczych wpływają na ocenę, jaką student otrzymuje z określonego egzaminu wstępnego na studia.
Aby zbadać tę zależność, możemy przeprowadzić wielokrotną regresję liniową, wykorzystując przepracowane godziny i egzaminy przygotowawcze traktowane jako zmienne objaśniające, a wyniki egzaminów jako zmienną odpowiedzi.
Wykonaj poniższe kroki w programie Excel, aby przeprowadzić wielokrotną regresję liniową.
Krok 1: Wprowadź dane.
Wprowadź następujące dane dotyczące liczby godzin nauki, zdanych egzaminów przygotowawczych i uzyskanych wyników egzaminów dla 20 uczniów:
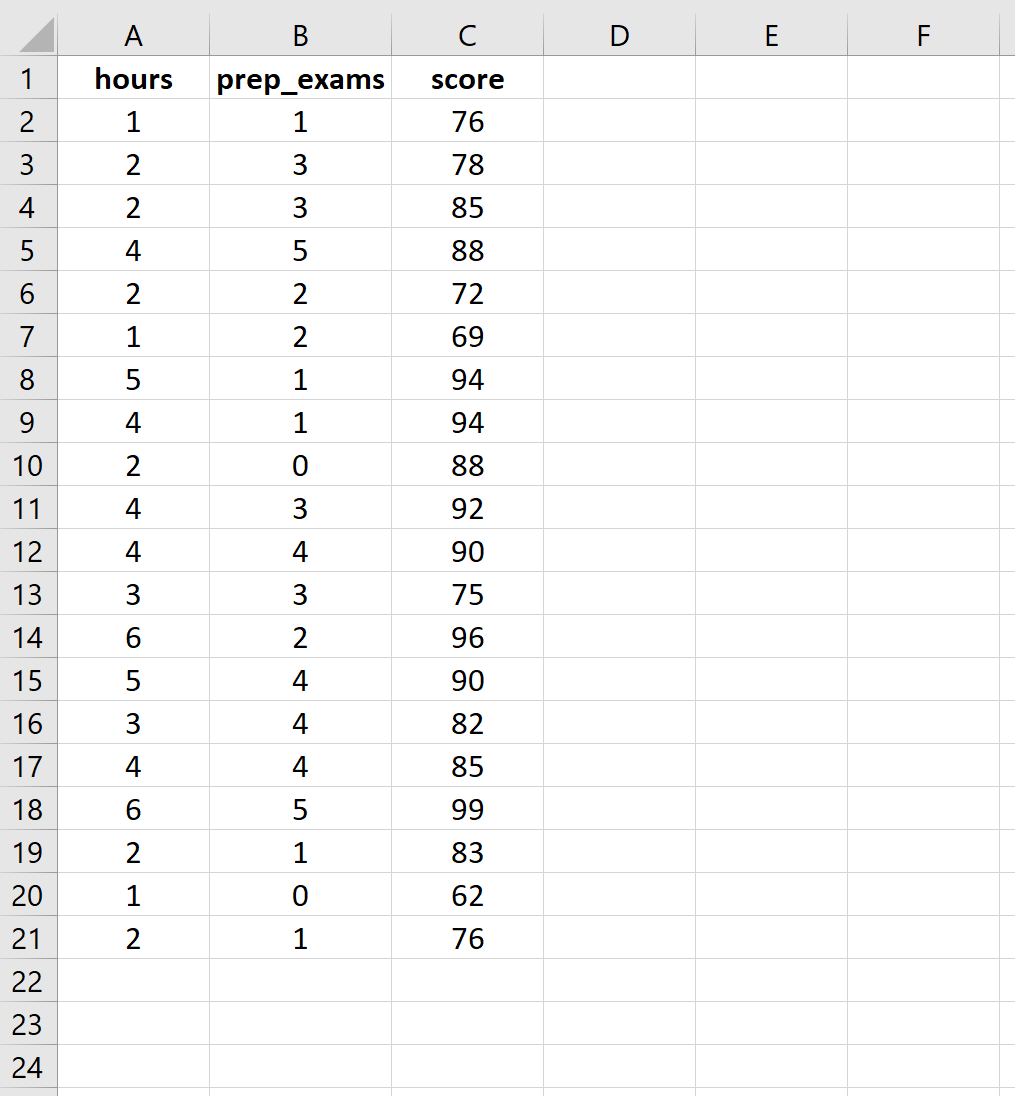
Krok 2: Wykonaj wielokrotną regresję liniową.
Na górnej wstążce programu Excel przejdź do karty Dane i kliknij opcję Analiza danych . Jeśli nie widzisz tej opcji, musisz najpierw zainstalować bezpłatne oprogramowanie Analysis ToolPak .

Po kliknięciu Analiza danych pojawi się nowe okno. Wybierz opcję Regresja i kliknij OK.
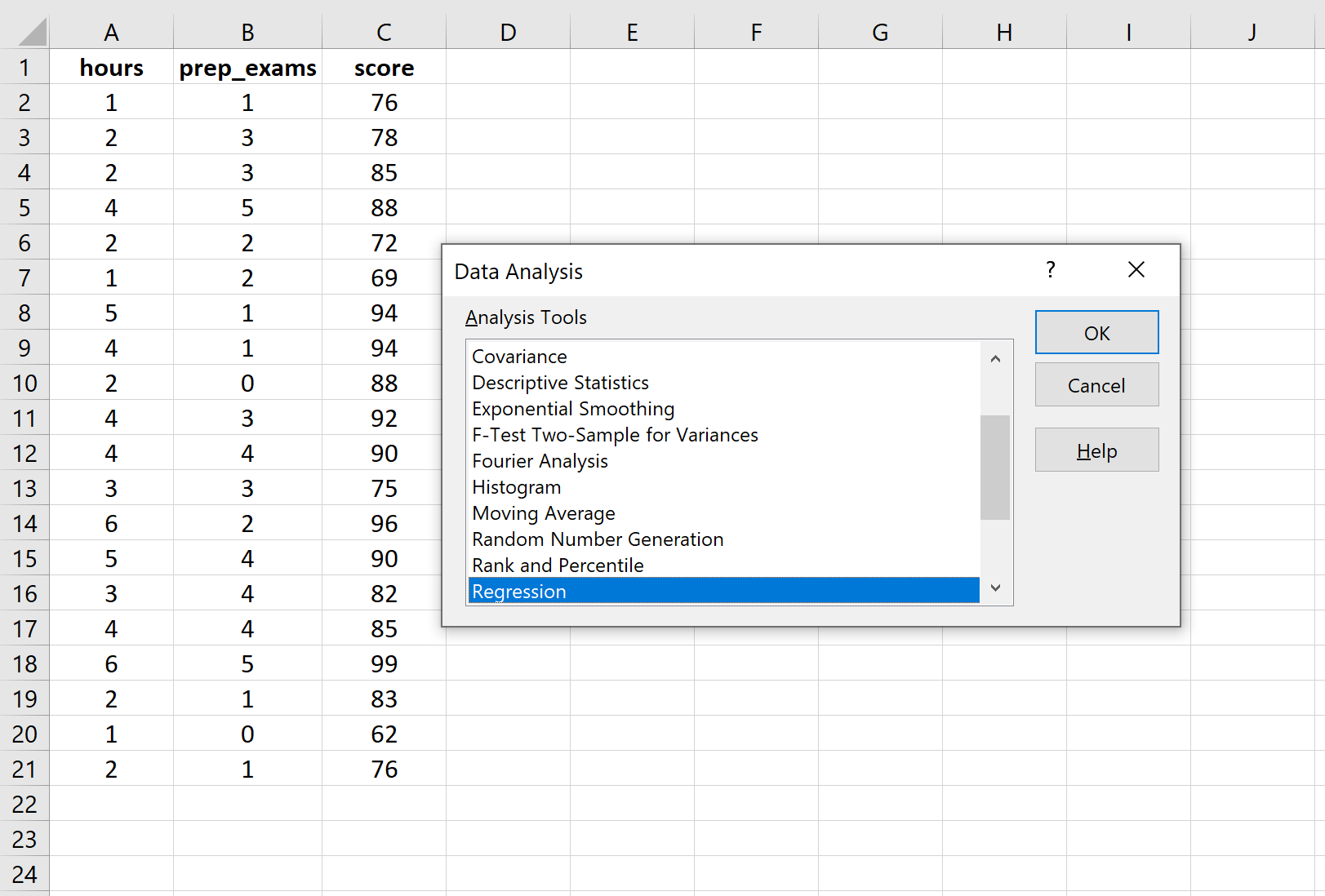
W polu Zakres wejściowy Y wypełnij tablicę wartości zmiennej odpowiedzi. W polu Zakres wejściowy X wypełnij tablicę wartości dla dwóch zmiennych objaśniających. Zaznacz pole obok Etykiet , aby program Excel wiedział, że uwzględniliśmy nazwy zmiennych w zakresach wejściowych. W polu Zakres wyjściowy wybierz komórkę, w której chcesz wyświetlić wynik regresji. Następnie kliknij OK .
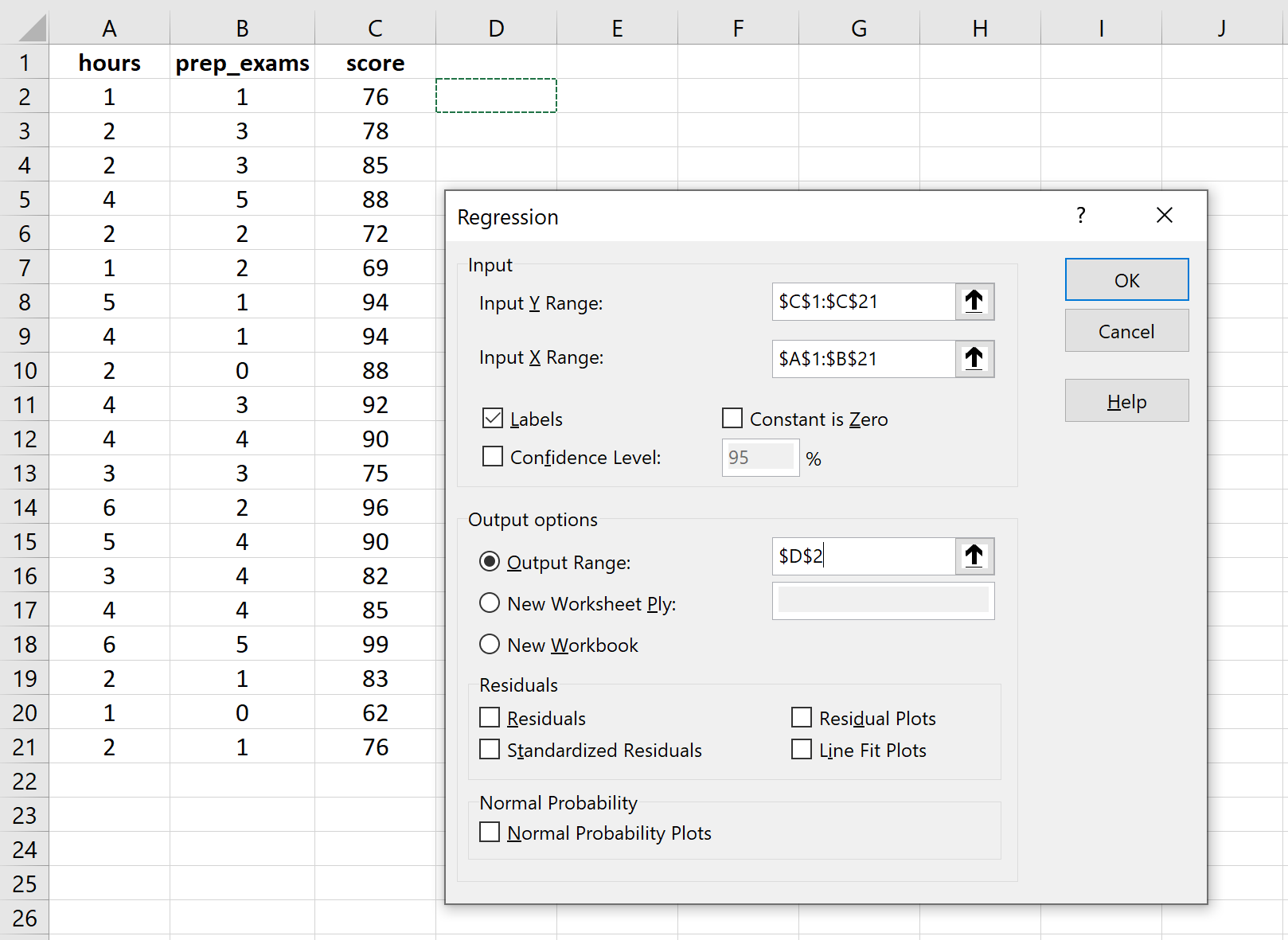
Następujące dane wyjściowe pojawią się automatycznie:

Krok 3: Zinterpretuj wynik.
Oto jak zinterpretować najbardziej odpowiednie liczby w wyniku:
R Kwadrat: 0,734 . Nazywa się to współczynnikiem determinacji. Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych objaśniających. W tym przykładzie 73,4% różnic w wynikach egzaminów można wytłumaczyć liczbą godzin nauki i liczbą zdanych egzaminów przygotowawczych.
Błąd standardowy: 5,366 . Jest to średnia odległość pomiędzy obserwowanymi wartościami a linią regresji. W tym przykładzie zaobserwowane wartości odbiegają średnio o 5366 jednostek od linii regresji.
F: 23:46 To jest ogólna statystyka F dla modelu regresji, obliczona jako MS regresji/MS rezydualne.
Znaczenie F: 0,0000 . Jest to wartość p powiązana z ogólną statystyką F. To mówi nam, czy model regresji jako całość jest statystycznie istotny, czy nie. Innymi słowy, mówi nam, czy dwie zmienne objaśniające łącznie mają statystycznie istotny związek ze zmienną odpowiedzi. W tym przypadku wartość p jest mniejsza niż 0,05, co wskazuje, że zmienne objaśniające , przepracowane godziny i zdane egzaminy przygotowawcze łącznie mają statystycznie istotny związek z wynikiem egzaminu .
Wartości P. Poszczególne wartości p mówią nam, czy każda zmienna objaśniająca jest istotna statystycznie, czy nie. Widzimy, że przepracowane godziny są istotne statystycznie (p = 0,00), natomiast zdane egzaminy przygotowawcze (p = 0,52) nie są istotne statystycznie przy α = 0,05. Ponieważ dotychczasowe egzaminy przygotowawcze nie są istotne statystycznie, może się okazać, że zdecydujemy się na ich usunięcie z modelu.
Współczynniki: Współczynniki każdej zmiennej objaśniającej mówią nam o oczekiwanej średniej zmianie zmiennej odpowiedzi, przy założeniu, że druga zmienna objaśniająca pozostaje stała. Na przykład za każdą dodatkową godzinę spędzoną na nauce średni wynik egzaminu powinien wzrosnąć o 5,56 , przy założeniu, że liczba zdanych egzaminów praktycznych pozostanie stała.
Spójrzmy na to z innego punktu widzenia: jeśli Student A i Student B zdają tę samą liczbę egzaminów przygotowawczych, ale Student A uczy się o godzinę dłużej, wówczas Student A powinien uzyskać o 5,56 punktu więcej niż uczeń B.
Interpretujemy współczynnik przechwytywania w ten sposób, że oczekiwany wynik egzaminu dla studenta, który nie studiuje i nie przystępuje do egzaminów przygotowawczych, wynosi 67,67 .
Szacowane równanie regresji: Możemy użyć współczynników z wyników modelu, aby utworzyć następujące szacunkowe równanie regresji:
wynik egzaminu = 67,67 + 5,56*(godziny) – 0,60*(egzaminy przygotowawcze)
Możemy użyć tego szacunkowego równania regresji do obliczenia oczekiwanego wyniku egzaminu dla studenta na podstawie liczby godzin nauki i liczby egzaminów praktycznych, które zdają. Przykładowo, student studiujący trzy godziny i przystępujący do egzaminu przygotowawczego powinien otrzymać ocenę 83,75 :
wynik egzaminu = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Należy pamiętać, że ponieważ poprzednie badania przygotowawcze nie były istotne statystycznie (p=0,52), możemy zdecydować się na ich usunięcie, gdyż nie wnoszą one żadnej poprawy w stosunku do ogólnego modelu. W tym przypadku moglibyśmy przeprowadzić prostą regresję liniową, wykorzystując jedynie badane godziny jako zmienną objaśniającą.
Wyniki tej prostej analizy regresji liniowej można znaleźć tutaj .
Dodatkowe zasoby
Po przeprowadzeniu wielokrotnej regresji liniowej warto sprawdzić kilka założeń, w tym:
1. Testowanie współliniowości za pomocą VIF .
2. Zbadaj heterodskedastyczność za pomocą testu Breuscha-Pagana .