Kwartyle

Przez Benjamin Anderson 5 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniamy, czym są kwartyle. Znajdziesz definicję każdego kwartyla, sposób jego obliczania i kilka konkretnych przykładów. Pokazujemy również, jak obliczyć kwartyle dla pogrupowanych danych. Dodatkowo za pomocą kalkulatora online będziesz mógł obliczyć kwartyle dowolnego zbioru danych.

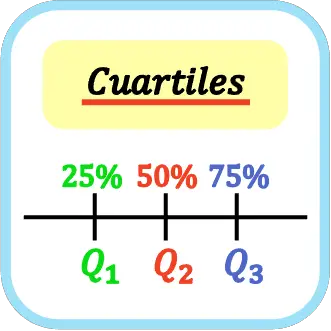
Co to są kwartyle?

W statystyce kwartyle to trzy wartości dzielące zbiór uporządkowanych danych na cztery równe części. Zatem pierwszy, drugi i trzeci kwartyl reprezentuje odpowiednio 25%, 50% i 75% wszystkich danych statystycznych.

Kwartyle są reprezentowane przez dużą literę Q i indeks kwartylowy, więc pierwszy kwartyl to Q ₁ , drugi kwartyl to Q ₂ , a trzeci kwartyl to Q ₃ .

👉 Za pomocą poniższego kalkulatora możesz obliczyć kwartyle dowolnego zbioru danych.

Należy zauważyć, że kwartyle są miarą położenia niecentralnego w taki sam sposób, jak kwintyle, decyle i percentyle. Możesz sprawdzić, czym jest każdy z tych typów kwantyli na tej stronie internetowej.

pierwszy kwartyl

Pierwszy kwartyl , zwany także kwartylem 1, to wartość większa niż 25% danych statystycznych w próbie. Innymi słowy, pierwszy kwartyl reprezentuje ponad 25% zaobserwowanych danych.

Pierwszy kwartyl wyrażany jest symbolem Q ₁ i służy do oznaczenia najmniejszych wartości danych w próbie.

drugi kwartyl

Drugi kwartyl , zwany także kwartylem 2, to wartość większa niż 50% danych statystycznych w próbie. Dlatego drugi kwartyl dzieli zbiór danych na dwie połowy i pokrywa się z medianą i piątym decylem.

Symbolem drugiego kwartyla jest _Q2 .

trzeci kwartyl

Trzeci kwartyl , zwany także trzecim kwartylem, to wartość przekraczająca 75% danych statystycznych w próbie. Innymi słowy, trzeci kwartyl reprezentuje ponad 75% zebranych danych.

Trzeci kwartyl wyrażony jest symbolem Q ₃ i reprezentuje największe wartości w próbie.

Jak obliczyć kwartyle

Aby obliczyć położenie kwartylów zbioru danych statystycznych, należy pomnożyć liczbę kwartylów przez sumę całkowitej liczby danych plus jeden i podzielić wynik przez cztery.

Wzór na kwartyle jest zatem następujący:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Uwaga: ten wzór informuje nas o pozycji kwartyla, a nie o jego wartości. Kwartylem będą dane znajdujące się na pozycji otrzymanej ze wzoru.

Czasami jednak wynik tej formuły da nam liczbę dziesiętną. Musimy zatem rozróżnić dwa przypadki w zależności od tego, czy wynik jest liczbą dziesiętną, czy nie:

Jeżeli wynikiem wzoru jest liczba bez części dziesiętnej , kwartylem jest dana, która znajduje się na pozycji określonej we wzorze powyżej.
Jeżeli wynikiem wzoru jest liczba zawierająca część dziesiętną , wartość kwartylowa obliczana jest według następującego wzoru:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Gdzie x _i oraz x _i+1 to numery pozycji, pomiędzy którymi znajduje się liczba uzyskana według pierwszego wzoru, a d to część dziesiętna liczby uzyskanej według pierwszego wzoru.

Być może obliczanie kwartylów jest dla Ciebie bardzo skomplikowane, ponieważ jest wiele rzeczy, które należy wziąć pod uwagę. Ale dzięki dwóm przykładom w następnej sekcji zobaczysz, że w rzeczywistości jest to całkiem proste.

Uwaga : w środowisku naukowym nie ma zgody co do sposobu obliczania kwartylów, dlatego można znaleźć książkę statystyczną, która wyjaśnia to nieco inaczej.

Przykłady obliczania kwartylów

Aby w pełni zrozumieć, w jaki sposób obliczane są kwartyle, poniżej znajdziesz dwa rozwiązane ćwiczenia. W pierwszym kwartyle są liczbami całkowitymi, a w drugim kwartyle są liczbami dziesiętnymi, więc możesz zobaczyć, które dwa przypadki znajdziesz.

Przykład 1

Oblicz trzy kwartyle następującego zbioru danych:

Jak widzieliśmy powyżej, wzór na określenie kwartylów jest następujący:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

W tym przypadku n całkowita liczba obserwacji wynosi 15, dlatego musimy zastąpić n przez 15, a k przez 1, aby znaleźć pierwszy kwartyl:

$\cfrac{1\cdot (15+1)}{4}=4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_1=39$

Zatem pierwszy kwartyl to liczba znajdująca się na czwartej pozycji uporządkowanej listy wartości, która w tym przypadku wynosi 39.

W ten sam sposób obliczamy drugi kwartyl, zastępując współczynnik k liczbą 2:

$\cfrac{2\cdot (15+1)}{4}=8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_2=48$

Kwartyl 2 jest zatem ósmą liczbą na posortowanej liście, która odpowiada wartości 48.

Na koniec po raz ostatni stosujemy wzór z k = 3, aby obliczyć trzeci kwartyl:

$\cfrac{3\cdot (15+1)}{4}=12 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_3=60$

Kwartyl 3 odpowiada danym znajdującym się na dwunastej pozycji, czyli 60.

Przykład 2

Znajdź trzy kwartyle następujących serii danych:

W tym drugim przykładzie mamy 24 obserwacje, więc liczby uzyskane ze wzoru kwartylowego będą dziesiętne.

Najpierw obliczamy położenie pierwszego kwartyla, podstawiając k za 1 we wzorze ogólnym:

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (24+1)}{4}=6,25$

Ale otrzymaliśmy liczbę dziesiętną 6,25, więc pierwszy kwartyl leży pomiędzy szóstą i siódmą daną, czyli odpowiednio 22 i 25. Dlatego, aby obliczyć dokładny kwartyl, należy zastosować następujący wzór:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

W tym przypadku x _i wynosi 22, x _i+1 25, a d jest częścią dziesiętną otrzymanej liczby, czyli 0,25. Już:

$Q_1=22+0,25\cdot (25-22)=22,75$

Teraz wykonujemy tę samą procedurę, aby znaleźć drugi kwartyl:

$\cfrac{2\cdot (24+1)}{4}=12,5$

Ponownie otrzymujemy liczbę dziesiętną ze wzoru, w tym przypadku jest to 12,5. Musimy zatem użyć tego samego wzoru z dwunastą i trzynastą liczbą w tabeli danych, co odpowiada 49 i 50:

$Q_2=49+0,5\cdot (50-49)=49,5$

Na koniec powtarzamy ten sam proces, aby uzyskać trzeci kwartyl:

$\cfrac{3\cdot (24+1)}{4}=18,75$

Ale liczba 18,75 znajduje się pomiędzy liczbą 18 a 19, więc trzeci kwartyl będzie pomiędzy wartościami tych pozycji (71 i 73). Dokładniej będzie to wartość, którą otrzymamy z następującego wyrażenia:

$Q_3=71+0,75\cdot (73-71)=72,5$

kalkulator kwartylowy

Podłącz zestaw danych statystycznych do kalkulatora poniżej, aby obliczyć kwartyle. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

Kwartyle w danych pogrupowanych

Aby obliczyć kwartyle, gdy dane są pogrupowane w przedziały, musimy najpierw znaleźć przedział lub przedział, w którym mieści się kwartyl, korzystając z następującego wzoru:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Kwartyl będzie zatem znajdował się w przedziale, którego bezwzględna skumulowana częstotliwość jest bezpośrednio większa niż liczba uzyskana za pomocą poprzedniego wyrażenia.

Kiedy już znamy przedział, do którego należy kwartyl, musimy zastosować następujący wzór, aby znaleźć dokładną wartość kwartyla:

$Q_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3$

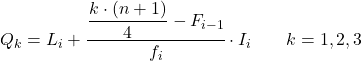
Złoto:

L _i jest dolną granicą przedziału, w którym leży kwartyl.
n to całkowita liczba obserwacji.
F _i-1 jest skumulowaną częstotliwością bezwzględną poprzedniego przedziału.
f _i jest częstotliwością bezwzględną przedziału, w którym leży kwartyl.
I _i jest szerokością przedziału kwartylowego.

Oto przykładowe ćwiczenie polegające na obliczeniu kwartylów w serii pogrupowanych danych:

Aby obliczyć pierwszy kwartyl, należy najpierw określić przedział, w którym on przypada. W tym celu stosujemy następujący wzór:

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (30+1)}{4} =7,75 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [50,60)$

Zatem pierwszy kwartyl będzie w przedziale, którego skumulowana częstotliwość bezwzględna jest bezpośrednio większa niż 7,75, w tym przypadku jest to przedział [50,60), którego skumulowana częstotliwość bezwzględna wynosi 15. Kiedy już znamy przedział kwartylowy, używamy drugiego wzoru na proces :

$Q_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i$

$Q_1=50+\cfrac{\displaystyle\frac{1\cdot (30+1)}{4}-7}{8}\cdot 10=50,94$

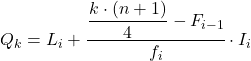
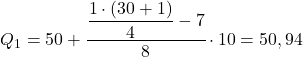
Stosujemy tę samą procedurę ponownie, aby uzyskać drugi kwartyl. Najpierw określamy przedział, w którym leży kwartyl:

$\cfrac{2\cdot (30+1)}{4} =15,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

Przedział, którego skumulowana częstotliwość bezwzględna jest bezpośrednio większa niż 15,5, wynosi [60,70), a skumulowana częstotliwość bezwzględna wynosi 26. Zatem drugi kwartyl to:

$Q_2=60+\cfrac{\displaystyle\frac{2\cdot (30+1)}{4}-15}{11}\cdot 10=60,45$

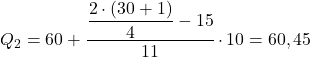
Na koniec powtarzamy proces, aby znaleźć trzeci kwartyl. Najpierw obliczamy przedział zawierający kwartyl:

$\cfrac{3\cdot (30+1)}{4} =22,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

Skumulowana częstotliwość bezwzględna bezpośrednio powyżej 23,25 wynosi 26, więc zakres trzeciego kwartyla wynosi [60,70). Dlatego stosujemy wzór do obliczenia kwartyla w tym przedziale:

$Q_3=60+\cfrac{\displaystyle\frac{3\cdot (30+1)}{4}-15}{11}\cdot 10=67,5$

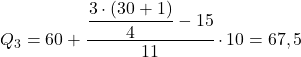
Do czego służą kwartyle?

Kwartyle są miarą położenia, dlatego służą do określania położenia danych. Innymi słowy, wartości trzech kwartylów pozwalają nam dowiedzieć się, czy losowy element danych w próbie jest bardzo duży, bardzo mały, czy też jest to wartość średnia.

Jeśli losowo pobierzemy fragment danych z próbki, możemy stwierdzić, czy jego wartość jest wysoka czy niska, porównując go z kwartylami. Jeśli wartość danych losowych jest mniejsza niż pierwszy kwartyl, będzie to wartość mała, natomiast jeśli jej wartość będzie większa niż trzeci kwartyl, będzie to wartość duża. Podobnie, jeśli wartość tych danych mieści się pomiędzy pierwszym a trzecim kwartylem, jest to wartość pośrednia.

Z drugiej strony kwartyle są również używane do obliczania innych miar statystycznych, takich jak rozstęp międzykwartylowy (lub rozstęp międzykwartylowy) oraz do tworzenia diagramów, takich jak wykres pudełkowy i wąsowy (lub wykres pudełkowy).

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Co to są kwartyle?

pierwszy kwartyl

drugi kwartyl

trzeci kwartyl

Jak obliczyć kwartyle

Przykłady obliczania kwartylów

Przykład 1

Przykład 2

kalkulator kwartylowy

Kwartyle w danych pogrupowanych

Do czego służą kwartyle?

o autorze

Dr Benjamin Anderson

Dodaj komentarz