Jak zastosować centralne twierdzenie graniczne w programie excel

Centralne twierdzenie graniczne stwierdza, że rozkład próbkowania średniej próbki jest w przybliżeniu normalny, jeśli wielkość próby jest wystarczająco duża, nawet jeśli rozkład populacji nie jest normalny .

Centralne twierdzenie graniczne stwierdza również, że rozkład próbkowania będzie miał następujące właściwości:

1. Średnia rozkładu próby będzie równa średniej rozkładu populacji:

x = μ

2. Odchylenie standardowe rozkładu próby będzie równe odchyleniu standardowemu populacji podzielonemu przez liczebność próby:

s = σ / √n

W tym samouczku wyjaśniamy, jak zastosować centralne twierdzenie graniczne w programie Excel do danego rozkładu.

Zastosowanie centralnego twierdzenia granicznego w programie Excel

Załóżmy, że mamy rozkład ze średnią 8 i odchyleniem standardowym 4 . Aby znaleźć zarówno średnią, jak i odchylenie standardowe rozkładu próbkowania przy próbie o wielkości 15 , możemy użyć następujących formuł w programie Excel:

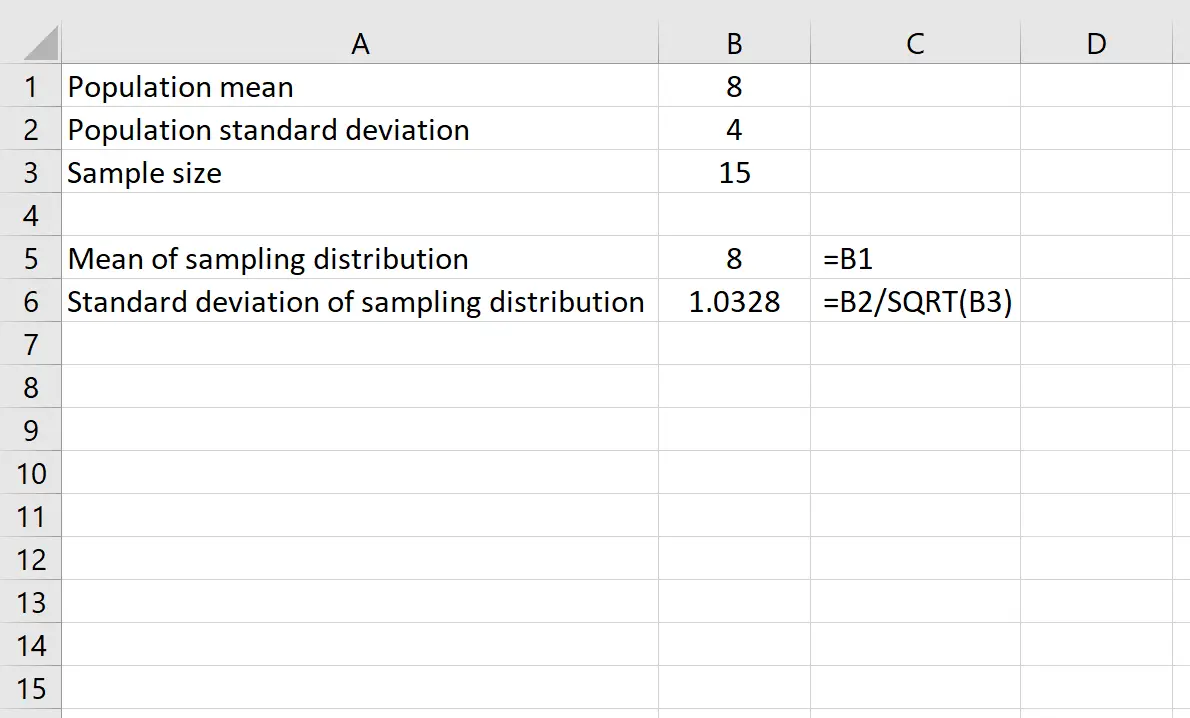
Średnia rozkładu próby jest po prostu równa średniej rozkładu populacji, która wynosi 8 .

Odchylenie standardowe rozkładu próbkowania jest równe odchyleniu standardowemu populacji podzielonemu przez wielkość próby, czyli: 4 /√15 = 1,0328 .

Centralnego twierdzenia granicznego możemy także użyć do odpowiedzi na pytania dotyczące prawdopodobieństwa. Na przykład, jeśli dana populacja ma średnią 8 i odchylenie standardowe 4 , jakie jest prawdopodobieństwo, że dana próba o liczebności 15   ma średnią mniejszą lub równą 7 ?

Aby odpowiedzieć na to pytanie, możemy użyć funkcji ROZKŁ.NORMALNY() w programie Excel, która wykorzystuje następującą składnię:

ROZKŁ.NORMALNY(x, średnia, odch.standardowa, skumulowany)

Złoto:

• x: próbka oznacza, że chcesz przetestować
• średnia: oczekiwana średnia rozkładu próbkowania
• standard_dev: oczekiwane odchylenie standardowe rozkładu próbkowania
• skumulowane: TRUE zwraca normalną wartość CDF; FAŁSZ zwraca wartość normalnego pliku PDF. W naszym przypadku zawsze będziemy używać TRUE.

Ta funkcja zwraca prawdopodobieństwo, że średnia próbki jest mniejsza lub równa określonej wartości.

Oto formuła, której użylibyśmy w tym przykładzie:

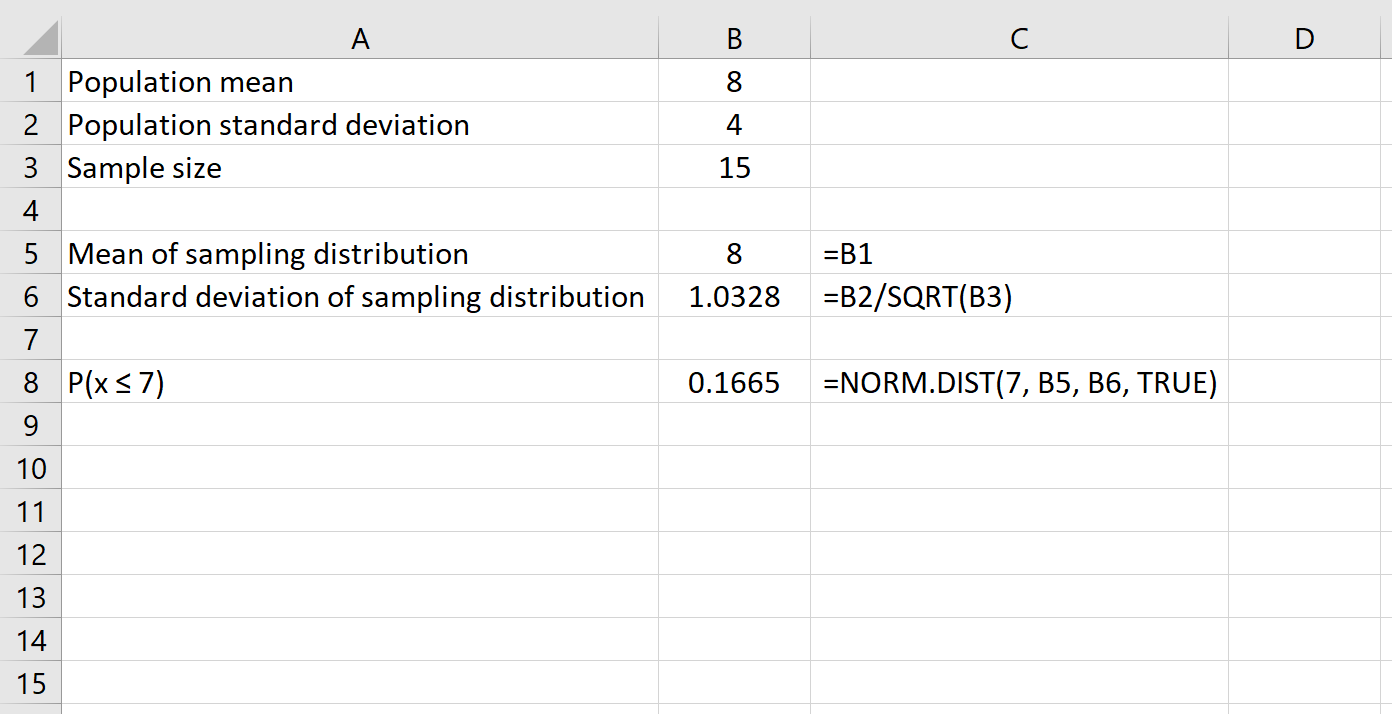
To mówi nam, że dla populacji o średniej wynoszącej 8 i odchyleniu standardowym wynoszącym 4 , prawdopodobieństwo, że dana próbka o wielkości 15   ma średnią mniejszą lub równą 7 lub 0,1665 .

Prawdopodobieństwo, że dana wielkość próbki będzie miała średnią większą niż określona liczba, możemy również obliczyć, po prostu używając wzoru 1 – ROZKŁ.NORMALNY() .

Na przykład poniższy wzór pokazuje, jak określić prawdopodobieństwo, że dla danej próby o liczebności 15 średnia będzie większa niż 7:

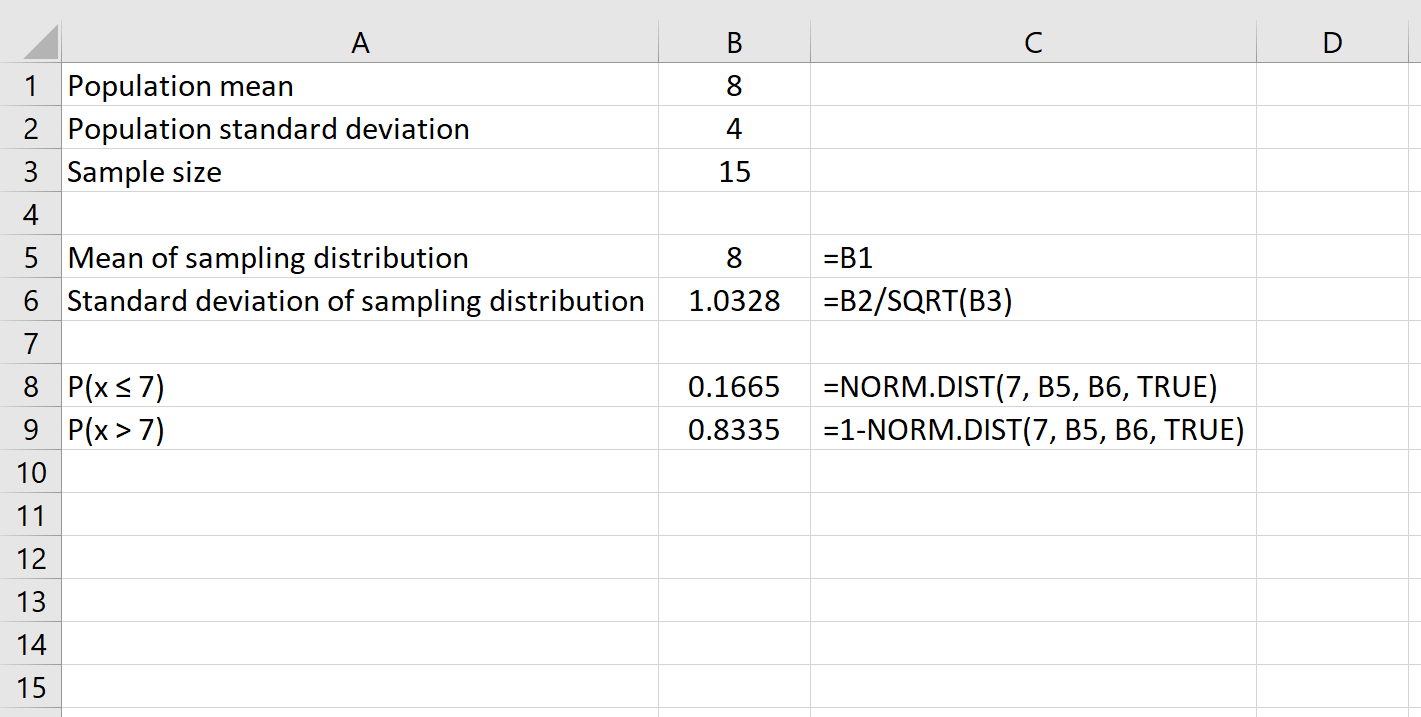
Na koniec możemy obliczyć prawdopodobieństwo, że dana wielkość próby ma średnią pomiędzy dwiema liczbami, korzystając ze wzoru ROZKŁ.NORMALNY(większa liczba) – ROZKŁ.NORMALNY(mniejsza liczba) .

Na przykład poniższy wzór pokazuje, jak znaleźć prawdopodobieństwo, że dla danej próby o liczebności 15 średnia mieści się w przedziale od 7 do 9:

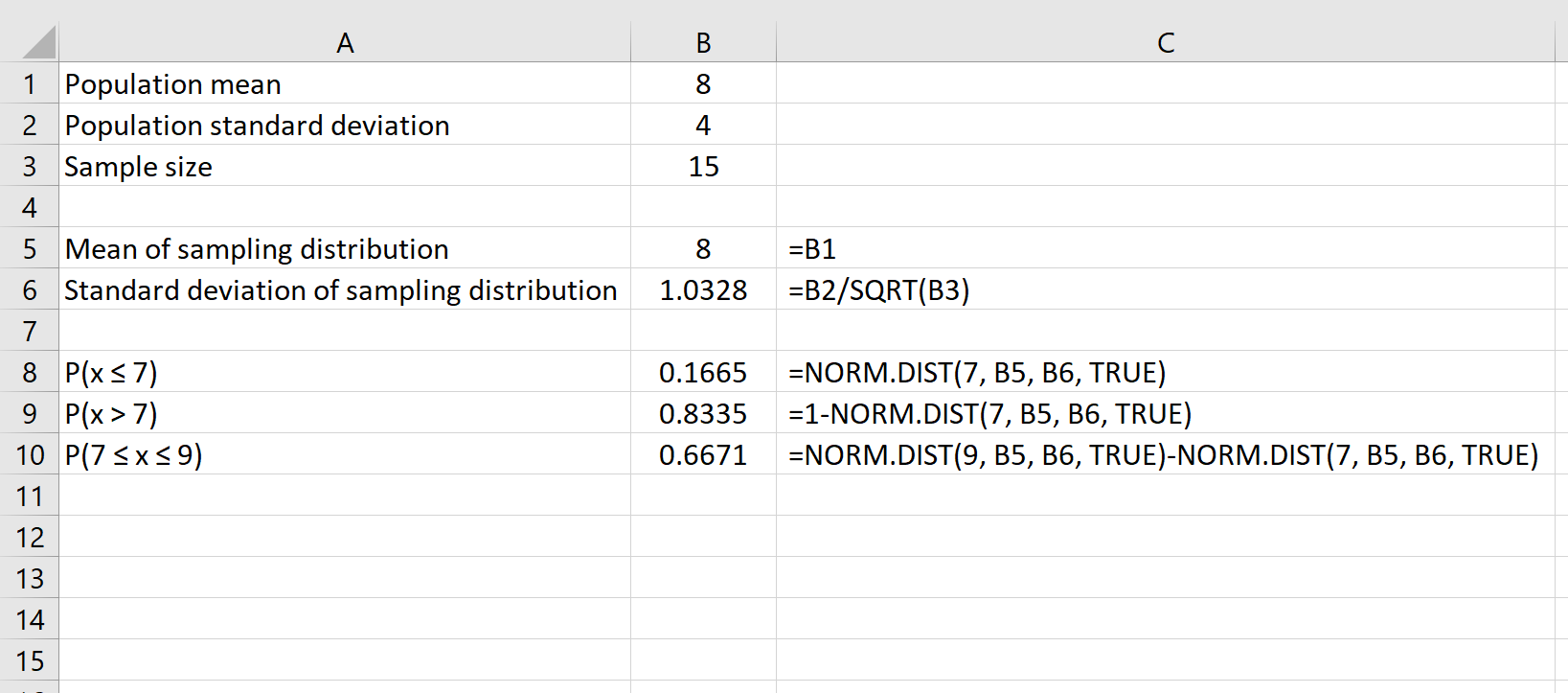
Dodatkowe zasoby

Kalkulator centralnego twierdzenia granicznego
Jak zastosować regułę praktyczną w programie Excel
Jak utworzyć krzywą dzwonową w programie Excel