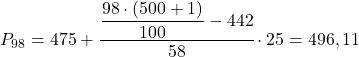Percentyle (statystyki)
W tym artykule wyjaśniono, czym jest percentyl i jak jest obliczany. Znajdziesz tu rozwiązane ćwiczenia dotyczące percentyli, a ponadto będziesz mógł obliczyć dowolny percentyl swojej próbki danych za pomocą kalkulatora online.
Co to są percentyle?
W statystyce percentyle to wartości dzielące zbiór uporządkowanych danych na sto równych części. Zatem percentyl wskazuje wartość, poniżej której spada procent zbioru danych.
Na przykład wartość 35. percentyla jest wyższa niż 35% obserwowanych danych, ale niższa niż pozostałe dane.
Percentyle są reprezentowane przez wielką literę P i indeks percentyla, co oznacza, że 1. percentyl to P 1 , 40. percentyl to P 40 , 79. percentyl to P 79 i tak dalej.

👉 Za pomocą poniższego kalkulatora możesz obliczyć percentyle dowolnego zbioru danych.
Podobnie percentyle są miarą położenia niecentralnego wraz z kwartylami, kwintylami i decylami. Znaczenie każdego z tych typów kwantyli możesz sprawdzić na naszej stronie internetowej.
Należy zauważyć, że terminu percentyle używa się również do porównania masy i wzrostu dziecka ze standardowymi wartościami innych dzieci, ponieważ istnieją tabele wzrostu z zarejestrowanymi wartościami, które pomagają określić, czy dziecko rośnie prawidłowo, czy nie. . .
Jak obliczyć percentyle
Aby obliczyć położenie percentyla serii danych statystycznych, należy pomnożyć liczbę percentyla przez sumę całkowitej liczby punktów danych plus jeden i podzielić wynik przez sto.
Zatem wzór percentylowy wygląda następująco:
![]()
Uwaga: ten wzór informuje nas o położeniu percentyla, ale nie o jego wartości. Percentylem będą dane znajdujące się na pozycji uzyskanej ze wzoru.
Czasami jednak wynik tej formuły da nam liczbę dziesiętną, dlatego musimy rozróżnić dwa przypadki w zależności od tego, czy wynik jest liczbą dziesiętną, czy nie:
- Jeżeli wynikiem wzoru jest liczba bez części dziesiętnej , percentylowi odpowiadają dane znajdujące się na pozycji podanej we wzorze powyżej.
- Jeśli wynikiem wzoru jest liczba z częścią dziesiętną , dokładna wartość percentyla jest obliczana przy użyciu następującego wzoru:
![]()
Gdzie x i oraz x i+1 to numery pozycji, pomiędzy którymi znajduje się liczba uzyskana według pierwszego wzoru, a d to część dziesiętna liczby uzyskanej według pierwszego wzoru.
Być może teraz myślisz, że znalezienie percentyli próby statystycznej lub populacji jest skomplikowane, ponieważ metoda ta obejmuje wiele etapów, ale w rzeczywistości jest łatwe. Przeczytaj poniższe dwa konkretne przykłady, a jestem pewien, że zrozumiesz to znacznie lepiej.
Uwaga : społeczność naukowa nie osiągnęła jeszcze całkowitej zgody co do sposobu obliczania percentyli, dlatego można znaleźć książkę statystyczną, która wyjaśnia to nieco inaczej.
Przykłady obliczeń percentylowych
Jak widzieliśmy powyżej w wyjaśnieniu, jak znaleźć percentyle próbki, obliczenia różnią się w zależności od tego, czy wynik pierwszego wzoru jest dziesiętny, czy nie. Dlatego poniżej znajdziesz dwa rozwiązane przykłady, po jednym dla każdego przypadku.
Przykład 1
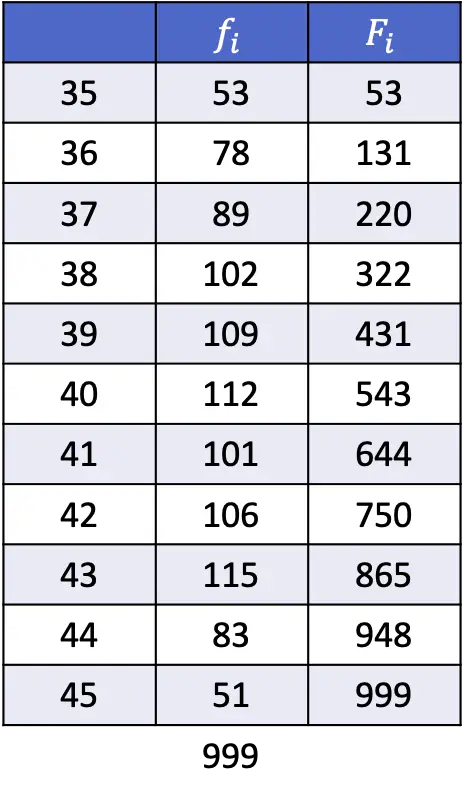
- Na podstawie danych przedstawionych w poniższej tabeli oblicz 1., 43. i 89. percentyl.
Jak wyjaśniono w poprzedniej sekcji, wzór na znalezienie położenia percentyla jest następujący:
![]()
W tym przypadku wielkość próby w tym ćwiczeniu wynosi 999 danych statystycznych, więc aby obliczyć położenie pierwszego percentyla, musimy zastąpić 999 za n i 1 za k :
![]()
Zatem pierwszym percentylem będzie ten, którego skumulowana częstotliwość bezwzględna jest bezpośrednio większa niż 10, co w tym przypadku wynosi 35, ponieważ jego skumulowana częstotliwość bezwzględna wynosi 53.
Aby określić 43. percentyl, należy użyć tego samego wzoru, ale oczywiście tym razem zastępujemy k przez 43.
![]()
Bezwzględna skumulowana częstotliwość bezpośrednio powyżej 430 wynosi 431 danych 39, więc 43. percentyl jest równy 39.
Na koniec stosujemy ten sam wzór, aby uzyskać 89. percentyl:
![]()
Skumulowana częstotliwość bezwzględna wartości 44 wynosi 948, czyli jest bezpośrednio większa niż 890. Zatem 89. percentyl wynosi 44.
Przykład 2
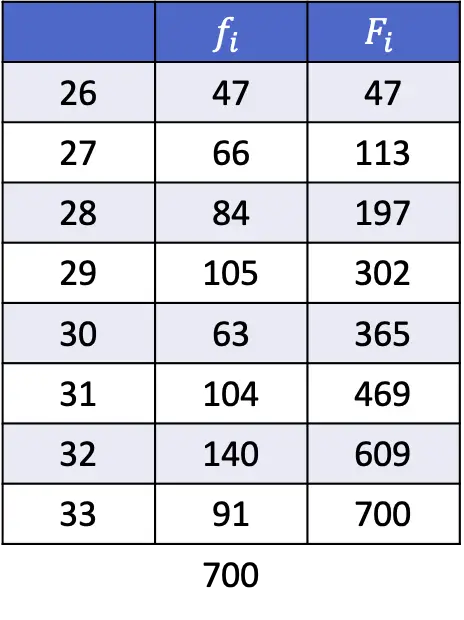
- Znajdź 35. i 67. percentyl w następujących seriach danych:
Nawet jeśli w tym ćwiczeniu będziemy musieli wykonać więcej obliczeń, zasada jest wciąż ta sama: musimy obliczyć położenie percentyla za pomocą następującego wyrażenia.
![]()
Zatem, aby obliczyć 35. percentyl, zastępujemy k przez 35, a n przez całkowitą liczbę danych, czyli 700:
![]()
Ale tym razem otrzymaliśmy liczbę dziesiętną ze wzoru, więc musimy zastosować następujące wyrażenie algebraiczne, aby obliczyć dokładną wartość percentyla:
![]()
Liczba podana w pierwszym wzorze wynosi 245,35, zatem 35. percentyl znajduje się pomiędzy pozycjami 245 i 246, co odpowiada odpowiednio wartościom 29 i 29. Zatem x i wynosi 29, x i+1 wynosi 29, a d jest wartością dziesiętnej części otrzymanej liczby, tj. 0,35.
![]()
Aby znaleźć 67. percentyl, musimy zastosować tę samą metodę. Najpierw obliczamy położenie percentyla:
![]()
Wynikowa liczba 469,67 wskazuje, że percentyl będzie znajdował się pomiędzy pozycjami 469 a 470, których wartości wynoszą 31 i 32. Dlatego w procesie używamy drugiego wzoru, aby znaleźć dokładną wartość percentyla:
![]()
kalkulator percentyla
Wprowadź zestaw danych statystycznych i liczbę percentylu, którą chcesz obliczyć, do poniższego kalkulatora. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.
Percentyle w pogrupowanych danych
Aby obliczyć percentyle, gdy dane są pogrupowane w grupy , musimy najpierw znaleźć grupę lub klasę, do której należy percentyl, korzystając z następującego wzoru:
![]()
Percentyl będzie zatem należeć do przedziału, którego częstotliwość bezwzględna jest bezpośrednio większa niż liczba uzyskana w poprzednim wyrażeniu.
A kiedy już znamy przedział, do którego należy percentyl, musimy zastosować następujący wzór, aby znaleźć dokładną wartość percentyla:
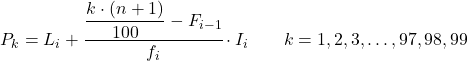
Złoto:
- L i jest dolną granicą przedziału, w którym leży percentyl.
- n to całkowita liczba obserwacji.
- F i-1 jest skumulowaną częstotliwością bezwzględną poprzedniego przedziału.
- f i jest częstotliwością bezwzględną przedziału, w którym leży percentyl.
- I i jest szerokością przedziału percentylowego.
Poniżej znajduje się ćwiczenie pokazujące krok po kroku, jak uzyskać percentyle, gdy dane są wyrażone w przedziałach. W szczególności obliczane są 29., 52. i 98. percentyl.

Dane w tej próbce są pogrupowane w przedziały, dlatego musimy wykonać dwa kroki, aby określić percentyle: najpierw musimy znaleźć przedział, w którym mieści się percentyl, a następnie zastosować wzór, aby obliczyć dokładną wartość percentyla. percentyl.
W ten sposób znajdujemy położenie 29. percentyla za pomocą następującego wyrażenia:
![]()
![]()
Przedziałem percentylowym będzie ten, którego skumulowana częstotliwość bezwzględna jest bezpośrednio większa niż 145,29, co w tym przypadku jest przedziałem [350,375), którego skumulowana częstotliwość bezwzględna wynosi 175. Kiedy już znamy przedział percentylowy, stosujemy następujący wzór do obliczenia jego Dokładna wartość:
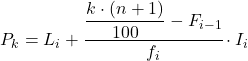
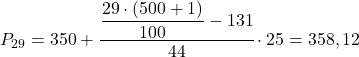
Teraz powtarzamy tę samą procedurę, aby obliczyć 52. percentyl. Najpierw obliczamy jego przedział:
![]()
Przedział 52. percentyla wynosi [400,425), ponieważ jego skumulowana częstotliwość bezwzględna (298) jest bezpośrednio powyżej 260,52. Dokładna wartość percentyla będzie zatem wynosić:
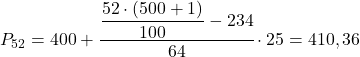
Wreszcie znajdziemy 98. percentyl. Jak zawsze, najpierw obliczamy przedział, w którym się on znajduje:
![]()
Kiedy już znamy przedział, w którym leży percentyl, obliczamy jego dokładną wartość za pomocą następującego wzoru: