Jak obliczyć prawdopodobieństwa normalne na kalkulatorze ti-84
Rozkład normalny jest najczęściej używanym rozkładem we wszystkich statystykach. W tym samouczku wyjaśniono, jak używać następujących funkcji kalkulatora TI-84 do znajdowania prawdopodobieństw rozkładu normalnego:
normalpdf(x, μ, σ) zwraca prawdopodobieństwo związane z normalnym plikiem PDF gdzie:
- x = wartość indywidualna
- μ = średnia populacji
- σ = odchylenie standardowe populacji
normalcdf(dolny_x, górny_x, μ, σ) zwraca skumulowane prawdopodobieństwo związane z normalnym cdf pomiędzy dwiema wartościami.
Złoto:
- dolna_x = niższa indywidualna wartość
- górna_x = górna wartość indywidualna
- μ = średnia populacji
- σ = odchylenie standardowe populacji
Te dwie funkcje są dostępne w kalkulatorze TI-84 po naciśnięciu 2., a następnie vars . Spowoduje to przejście do ekranu DISTR , na którym możesz użyć funkcji normalpdf() i normalcdf() :
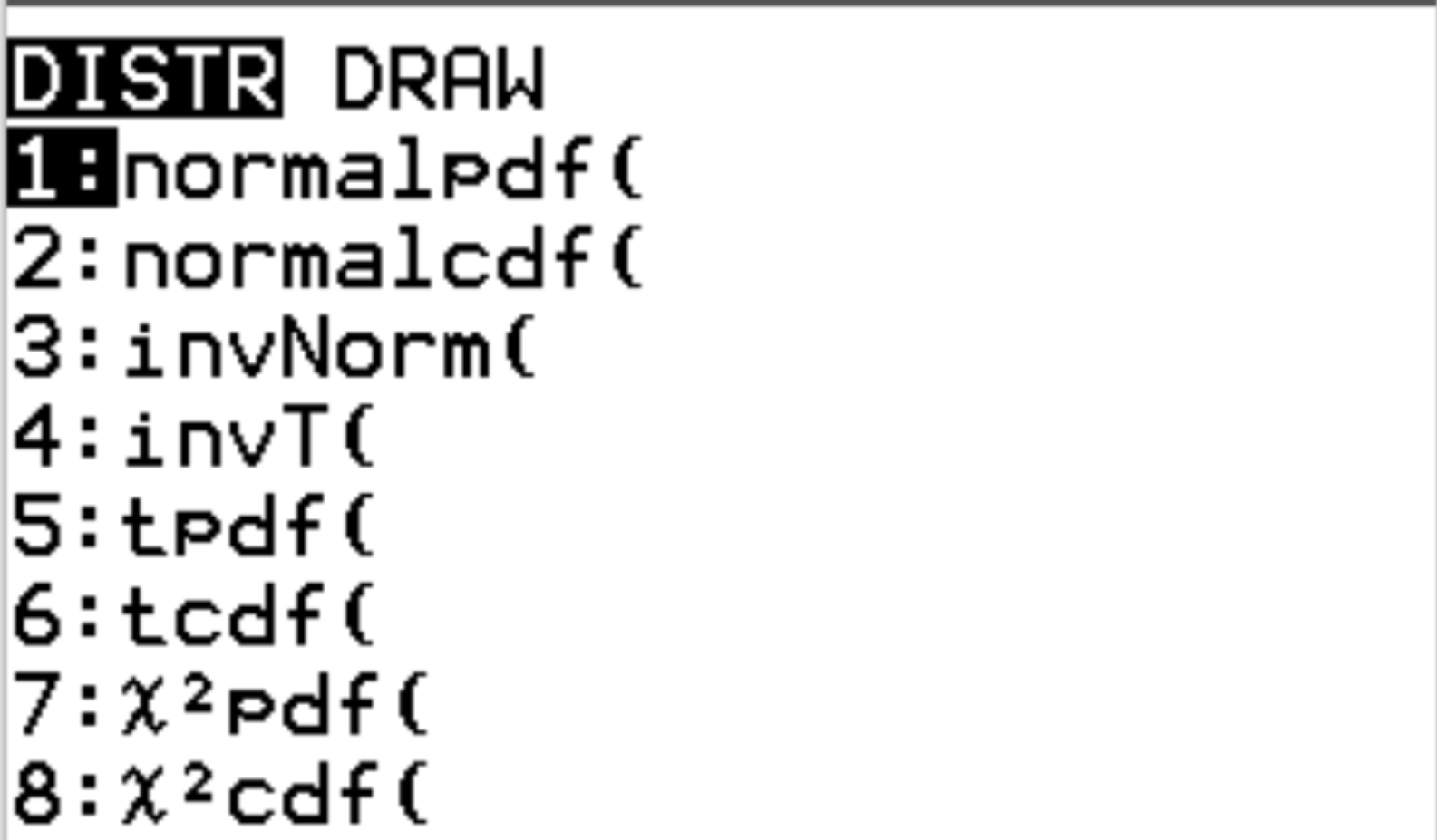
Poniższe przykłady ilustrują, jak używać tych funkcji do odpowiadania na różne pytania.
Przykład 1: prawdopodobieństwo normalne większe niż x
Pytanie: Dla rozkładu normalnego ze średnią = 40 i odchyleniem standardowym = 6 znajdź prawdopodobieństwo, że wartość będzie większa niż 45.
Odpowiedź: Użyj funkcji normalcdf(x, 10000, μ, σ):
normalcdf(45, 10000, 40, 6) = 0,2023
Uwaga: Ponieważ funkcja wymaga wartości Upper_x, użyjemy po prostu 10 000.
Przykład 2: prawdopodobieństwo normalne mniejsze niż x
Pytanie: Dla rozkładu normalnego ze średnią = 100 i odchyleniem standardowym = 11,3 znajdź prawdopodobieństwo, że wartość będzie mniejsza niż 98.
Odpowiedź: Użyj funkcji normalcdf(-10000, x, μ, σ):
normalcdf(-10000; 98; 100; 11,3) = 0,4298
Uwaga: Ponieważ funkcja wymaga wartości less_x, po prostu używamy -10000.
Przykład 3: Normalne prawdopodobieństwo między dwiema wartościami
Pytanie: Dla rozkładu normalnego ze średnią = 50 i odchyleniem standardowym = 4 znajdź prawdopodobieństwo, że wartość mieści się w przedziale od 48 do 52.
Odpowiedź: Użyj funkcji normalcdf(smaller_x, Larger_x, μ, σ)
normalcdf(48, 52, 50, 4) = 0,3829
Przykład 4: Normalne prawdopodobieństwo oprócz dwóch wartości
Pytanie: Dla rozkładu normalnego ze średnią = 22 i odchyleniem standardowym = 4 znajdź prawdopodobieństwo, że wartość będzie mniejsza niż 20 lub większa niż 24.
Odpowiedź: Użyj funkcji normalcdf(-10000, small_x, μ, σ) + normalcdf(larger_x, 10000, μ, σ)
normalcdf(-10000, 20, 22, 4) + normalcdf(24, 10000, 22, 4) = 0,6171