Przedział ufności dla różnicy między średnimi
Przedział ufności (CI) dla różnicy między średnimi to zakres wartości, który prawdopodobnie będzie zawierał prawdziwą różnicę między dwiema średnimi populacji przy pewnym poziomie ufności.
W tym samouczku wyjaśniono następujące kwestie:
- Motywacja do utworzenia tego przedziału ufności.
- Wzór do utworzenia tego przedziału ufności.
- Przykład obliczenia tego przedziału ufności.
- Jak interpretować ten przedział ufności.
CI dla różnicy pomiędzy środkami: motywacja
Naukowcy często chcą oszacować różnicę między średnimi dwóch populacji. Aby oszacować tę różnicę, pobiorą losową próbkę z każdej populacji i obliczą średnią dla każdej próbki. Następnie mogą porównać różnicę między dwiema średnimi.
Nie mogą jednak wiedzieć na pewno, czy różnica między średnimi z próby odpowiada rzeczywistej różnicy między średnimi z populacji. Dlatego mogą stworzyć przedział ufności dla różnicy między tymi dwoma średnimi. Zapewnia to zakres wartości, który prawdopodobnie będzie zawierał rzeczywistą różnicę między średnimi populacji.
Załóżmy na przykład, że chcemy oszacować różnicę w średniej masie dwóch różnych gatunków żółwi. Ponieważ w każdej populacji są tysiące żółwi, obchodzenie i ważenie każdego żółwia z osobna byłoby zbyt czasochłonne i kosztowne.
Zamiast tego moglibyśmy pobrać prostą losową próbkę 15 żółwi z każdej populacji i użyć średniej masy każdej próbki do oszacowania prawdziwej różnicy w średniej masie między dwiema populacjami:
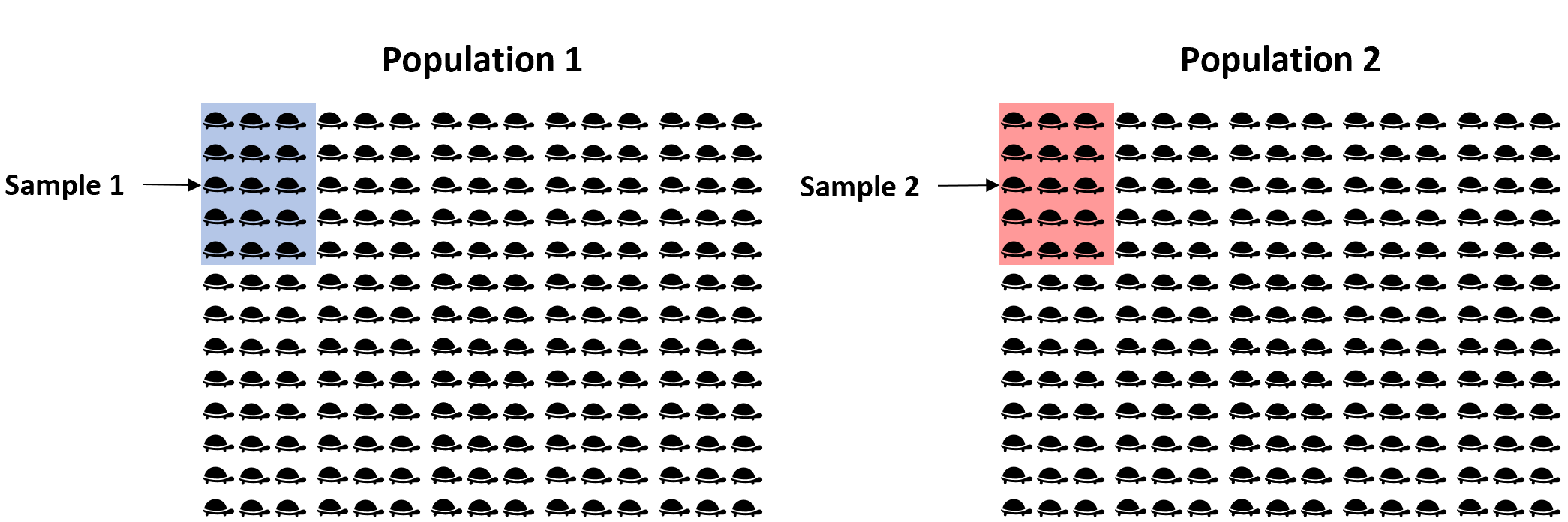
Problem polega na tym, że nasze próbki są losowe, więc nie ma gwarancji, że różnica średniej masy między dwiema próbkami dokładnie odpowiada różnicy średniej masy między dwiema populacjami. Aby więc uchwycić tę niepewność, możemy utworzyć przedział ufności zawierający zakres wartości, które prawdopodobnie zawierają prawdziwą różnicę średniej wagi między dwiema populacjami.
CI dla różnicy między średnimi: wzór
Aby obliczyć przedział ufności dla różnicy między dwiema średnimi, stosujemy następujący wzór:
Przedział ufności = ( x 1 – x 2 ) +/- t*√((s p 2 /n 1 ) + (s p 2 /n 2 ))
Złoto:
- x 1 , x 2 : średnia z próbki 1, średnia z próbki 2
- t: wartość krytyczna t oparta na poziomie ufności i (n 1 + n 2 -2) stopniach swobody
- s p 2 : wariancja zbiorcza
- n 1 , n 2 : wielkość próby 1, wielkość próby 2
Złoto:
- Łączną wariancję oblicza się w następujący sposób: s p 2 = ((n 1 -1) s 1 2 + (n 2 -1) s 2 2 ) / (n 1 + n 2 -2)
- Wartość krytyczną t t można znaleźć za pomocą kalkulatora odwrotnego rozkładu t.
CI dla różnicy pomiędzy średnimi: przykład
Załóżmy, że chcemy oszacować różnicę w średniej masie dwóch różnych gatunków żółwi. Dlatego z każdej populacji pobierzemy losową próbkę składającą się z 15 żółwi. Oto podsumowanie danych dla każdej próbki:
Próbka 1:
- x1 = 310
- s 1 = 18,5
- n 1 = 15
Próbka 2:
- x2 = 300
- s2 = 16,4
- n2 = 15
Oto jak znaleźć różne przedziały ufności dla prawdziwej różnicy średnich wag populacji:
90% przedział ufności:
(310-300) +/- 1,70*√((305,61/15) + (305,61/15)) = [-0,8589, 20,8589]
95% przedział ufności:
(310-300) +/- 2,05*√((305,61/15) + (305,61/15)) = [-3,0757, 23,0757]
99% przedział ufności:
(310-300) +/- 2,76*√((305,61/15) + (305,61/15)) = [-7,6389, 27,6389]
Uwaga: te przedziały ufności można również znaleźć za pomocą kalkulatora statystycznego przedziału ufności dla różnicy między średnimi .
Zauważysz, że im wyższy poziom ufności, tym szerszy przedział ufności. Powinno to mieć sens, ponieważ szersze przedziały z większym prawdopodobieństwem zawierają prawdziwą średnią populacji, więc mamy większą „pewność”, że przedział zawiera prawdziwą średnią populacji.
CI dla różnicy pomiędzy średnimi : interpretacja
Sposób, w jaki interpretujemy przedział ufności, wygląda następująco:
Istnieje 95% szans, że przedział ufności [-3,0757, 23,0757] zawiera prawdziwą różnicę w średniej masie ciała pomiędzy dwiema populacjami żółwi.
Ponieważ przedział ten zawiera wartość „0”, oznacza to, że możliwe jest, że nie ma różnicy w średniej masie pomiędzy żółwiami z tych dwóch populacji. Innymi słowy, nie możemy stwierdzić z 95% pewnością, że istnieje różnica w średniej wadze pomiędzy żółwiami z tych dwóch populacji.