Średnia różnica
W tym artykule wyjaśniono, czym jest odchylenie średnie i jak jest obliczane. Znajdziesz tu także konkretne przykłady obliczania średniego odchylenia. Co więcej, za pomocą kalkulatora online będziesz mógł obliczyć średnie odchylenie dowolnego zestawu danych statystycznych.
Co to jest średnie odchylenie?
Średnie odchylenie , zwane także średnim odchyleniem bezwzględnym , jest miarą rozproszenia statystycznego.
Średnie odchylenie zbioru danych jest średnią odchyleń bezwzględnych . Dlatego też średnie odchylenie jest równe sumie odchyleń każdego elementu danych od średniej arytmetycznej podzielonej przez całkowitą liczbę elementów danych.
Innymi słowy, wzór na średnie odchylenie jest następujący:

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć średnie odchylenie dowolnego zbioru danych.
W statystyce średnie odchylenie nazywane jest również średnim odchyleniem bezwzględnym .
Interpretacji średniego odchylenia dokonuje się w następujący sposób: im większa jest wartość średniego odchylenia, oznacza to, że dane są średnio dalej od średniej arytmetycznej; i odwrotnie, im niższe średnie odchylenie, tym bliższa jest wartość. dane są. Średnie odchylenie wskazuje zatem na rozproszenie serii danych.
Inne miary uważane za rozproszone to rozstęp, rozstęp międzykwartylowy, odchylenie standardowe (lub odchylenie standardowe), wariancja i współczynnik zmienności.
Jak obliczyć średnie odchylenie
Aby obliczyć średnie odchylenie serii danych, należy wykonać następujące kroki:
- Oblicz średnią arytmetyczną zbioru danych statystycznych.
- Oblicz odchylenie każdego punktu danych od średniej, zdefiniowanej jako wartość bezwzględna różnicy między danymi a średnią.
- Dodaj wszystkie różnice obliczone w poprzednim kroku.
- Podziel przez całkowitą liczbę danych. Otrzymany wynik jest średnim odchyleniem serii danych.
Podsumowując, wzór, który należy zastosować, aby znaleźć średnie odchylenie, to:
![]()
Przykład obliczenia średniego odchylenia
Biorąc pod uwagę definicję średniego odchylenia, poniżej znajduje się krok po kroku rozwiązany przykład obliczenia średniego odchylenia próby statystycznej. W ten sposób lepiej zrozumiesz, jak uzyskać średnie odchylenie.
- Analityk bada wyniki ekonomiczne firmy w ciągu ostatniego roku i posiada informacje na temat zysku osiągniętego przez spółkę w każdym kwartale tego roku: 2, 3, 7 i 5 milionów dolarów. Jakie jest średnie odchylenie danych?
Najpierw musimy uśrednić dane, więc sumujemy i dzielimy przez całkowitą liczbę obserwacji (4):
![]()
Po obliczeniu średniej arytmetycznej korzystamy ze wzoru na odchylenie średniej:
![]()
Podstawiamy dane do wzoru:
![]()
Obliczenia wykonujemy w liczniku:
![]()
![]()
![]()
Na koniec dzielimy przez całkowitą liczbę danych, aby uzyskać średnie odchylenie próbki:
![]()
Kalkulator średniego odchylenia
Wprowadź zestaw danych statystycznych do poniższego kalkulatora, aby obliczyć jego średnie odchylenie. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.
Średnie odchylenie dla danych pogrupowanych
Aby obliczyć średnie odchylenie danych pogrupowanych w przedziały, należy wykonać następujące kroki:
- Wyznacz średnią arytmetyczną zbioru danych statystycznych. Ponieważ dane są pogrupowane, wyrażenie służące do obliczenia średniej to:
- Oblicz odchylenie każdego przedziału od średniej, które jest równoważne wartości bezwzględnej różnicy między oceną klasy a średnią.
- Pomnóż odchylenie każdego przedziału przez jego częstotliwość bezwzględną.
- Dodaj wszystkie wyniki z poprzedniego kroku, a następnie podziel przez całkowitą liczbę danych. Otrzymany wynik jest średnim odchyleniem próbki pogrupowanej w przedziały.
![]()
![]()
![]()
![]()
Podsumowując, wzór na uzyskanie średniego odchylenia od zgrupowanych danych jest następujący:
![]()
Grupowanie danych oznacza zwykle, że jest ich dużo i znalezienie średniego odchylenia wymaga wielu etapów. Dlatego do obliczeń zwykle stosuje się tabele częstości.
Poniżej znajduje się ćwiczenie krok po kroku dotyczące obliczania średniego odchylenia, gdy dane są pogrupowane w przedziały:
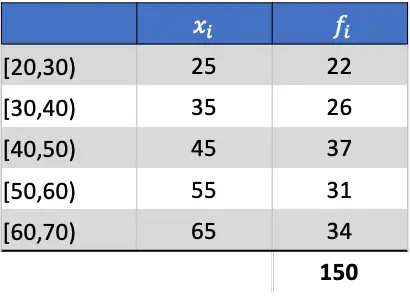
Pierwszą rzeczą do zrobienia jest obliczenie średniej z pogrupowanych danych. Aby to zrobić, dodajemy kolumnę do tabeli, mnożąc notatkę z zajęć przez jej częstotliwość:
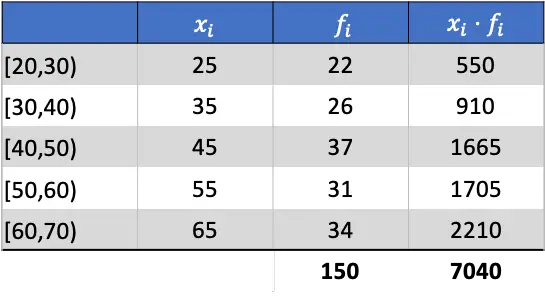
Średnia arytmetyczna będzie zatem wynikiem podzielenia sumy dodanej kolumny przez sumę częstotliwości bezwzględnych:
![]()
Teraz, gdy znamy średnią danych, możemy dodać wszystkie niezbędne kolumny, aby znaleźć średnie odchylenie:
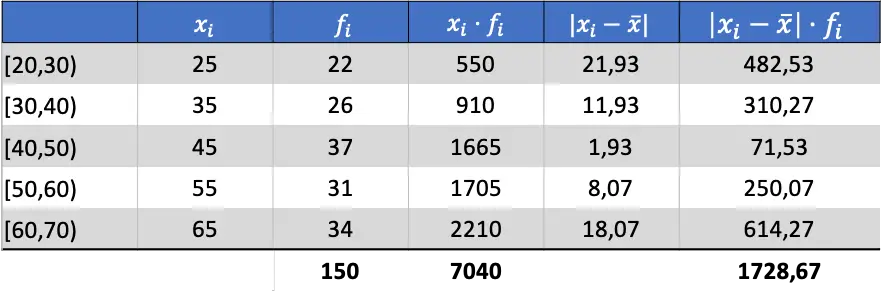
Zatem, aby otrzymać średnie odchylenie należy podzielić sumę z ostatniej kolumny przez całkowitą liczbę obserwacji:
![]()