Jak czytać tabelę rozkładu dwumianowego

Tabela rozkładu dwumianowego   to tabela pokazująca prawdopodobieństwa związane z rozkładem dwumianowym . Aby skorzystać z tabeli rozkładu dwumianowego, potrzebujesz tylko trzech wartości:

• n: liczba prób
• r: liczba „sukcesów” podczas n prób
• p: prawdopodobieństwo powodzenia danej próby

Korzystając z tych trzech liczb, możesz skorzystać z tabeli rozkładu dwumianowego, aby znaleźć prawdopodobieństwo uzyskania dokładnie r sukcesów w ciągu n prób, gdy prawdopodobieństwo sukcesu w każdej próbie wynosi p .

Poniższe przykłady ilustrują sposób odczytywania tabeli rozkładu dwumianowego.

Przykład 1

Pytanie: Jessica wykonuje 60% swoich prób rzutów wolnych. Jeśli wykona 6 rzutów wolnych, jakie jest prawdopodobieństwo, że trafi dokładnie 4?

Aby odpowiedzieć na to pytanie, możemy znaleźć wartość w tabeli rozkładu dwumianowego, która odpowiada n = 6, r = 4 i p = 0,60:

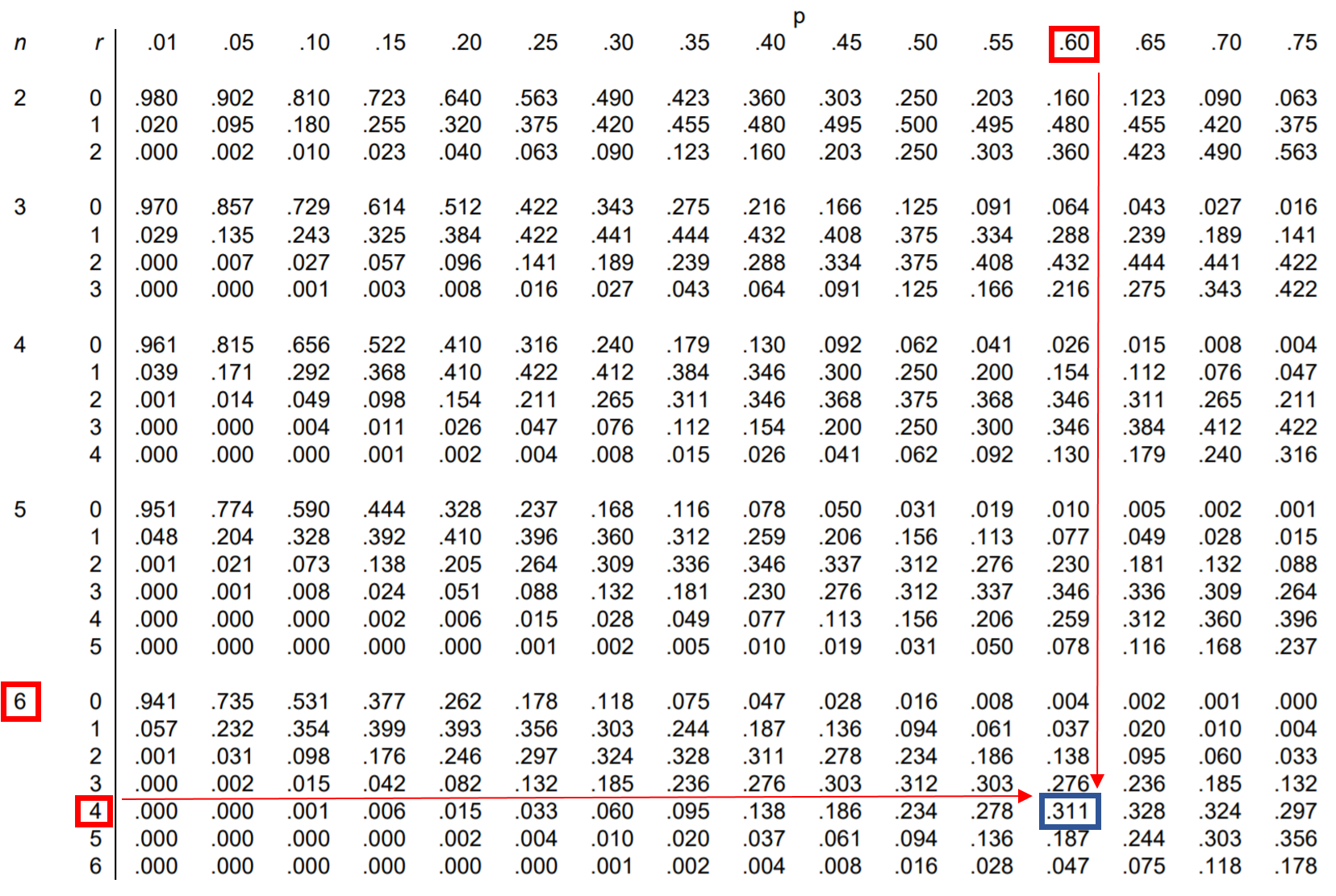
Prawdopodobieństwo, że Jessica wykona dokładnie 4 z 6 rzutów wolnych, wynosi 0,311 .

Przykład 2

Pytanie: Jessica wykonuje 60% swoich prób rzutów wolnych. Jeśli wykona 6 rzutów wolnych, jakie jest prawdopodobieństwo, że wykona mniej niż 4?

Aby znaleźć to prawdopodobieństwo, musisz dodać następujące prawdopodobieństwa:

P (daje mniej niż 4) = P (daje 0) + P (daje 1) + P (daje 2) + P (daje 3)

Możemy więc sprawdzić każde z tych czterech prawdopodobieństw w tabeli rozkładu dwumianowego i dodać je do siebie:

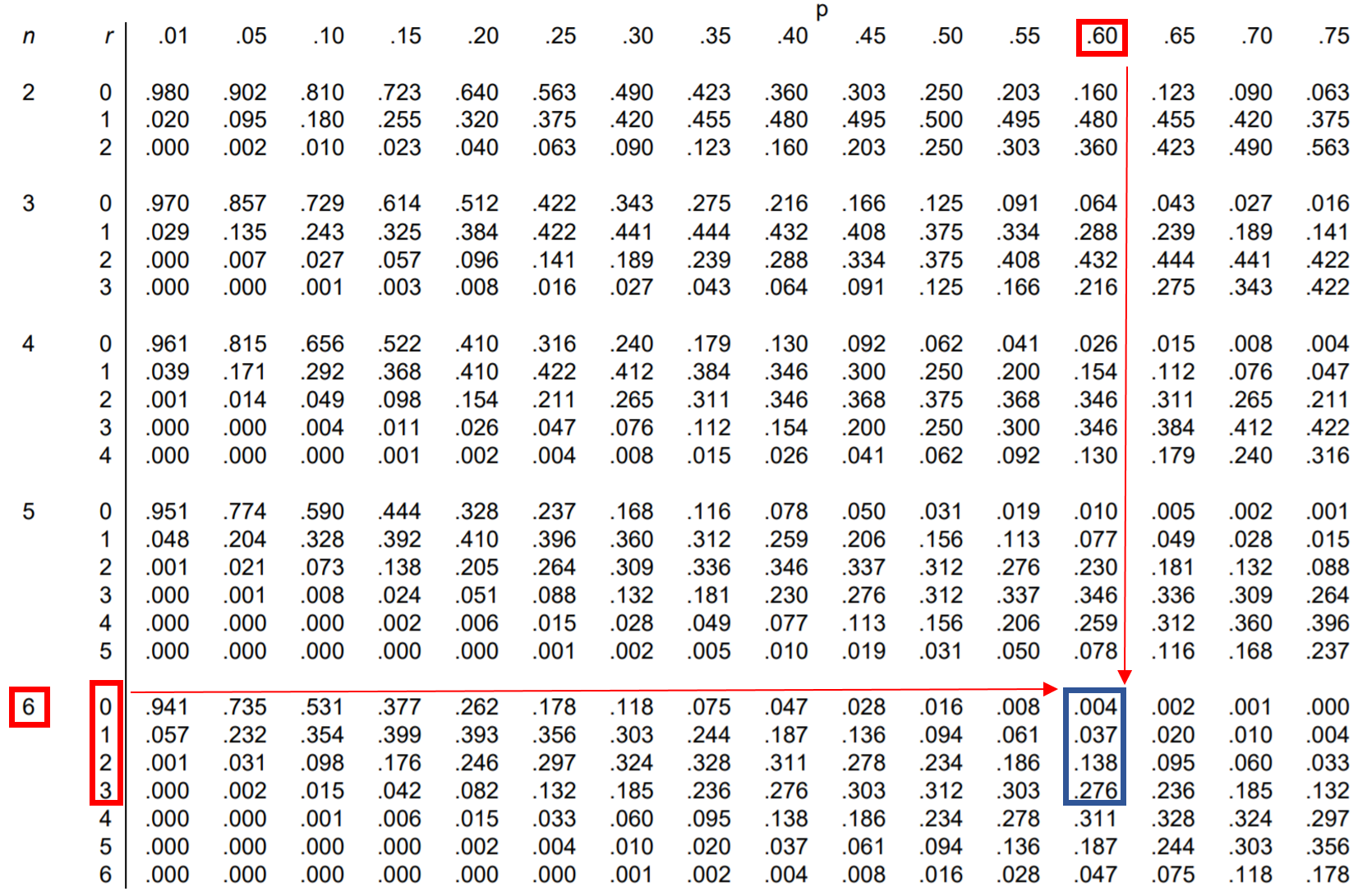
Z tabeli P(jest mniejsze niż 4) = 0,004 + 0,037 + 0,138 + 0,276 = 0,455 .

Prawdopodobieństwo, że Jessica wykona mniej niż 4 rzuty wolne, wynosi 0,455 .

Przykład 3

Pytanie: Jessica wykonuje 60% swoich prób rzutów wolnych. Jeśli wykona 6 rzutów wolnych, jakie jest prawdopodobieństwo, że trafi 4 lub więcej?

Aby znaleźć to prawdopodobieństwo, musimy dodać następujące prawdopodobieństwa:

P (daje 4 lub więcej) = P (daje 4) + P (daje 5) + P (daje 6)

Możemy więc sprawdzić każde z tych trzech prawdopodobieństw w tabeli rozkładu dwumianowego i dodać je do siebie:

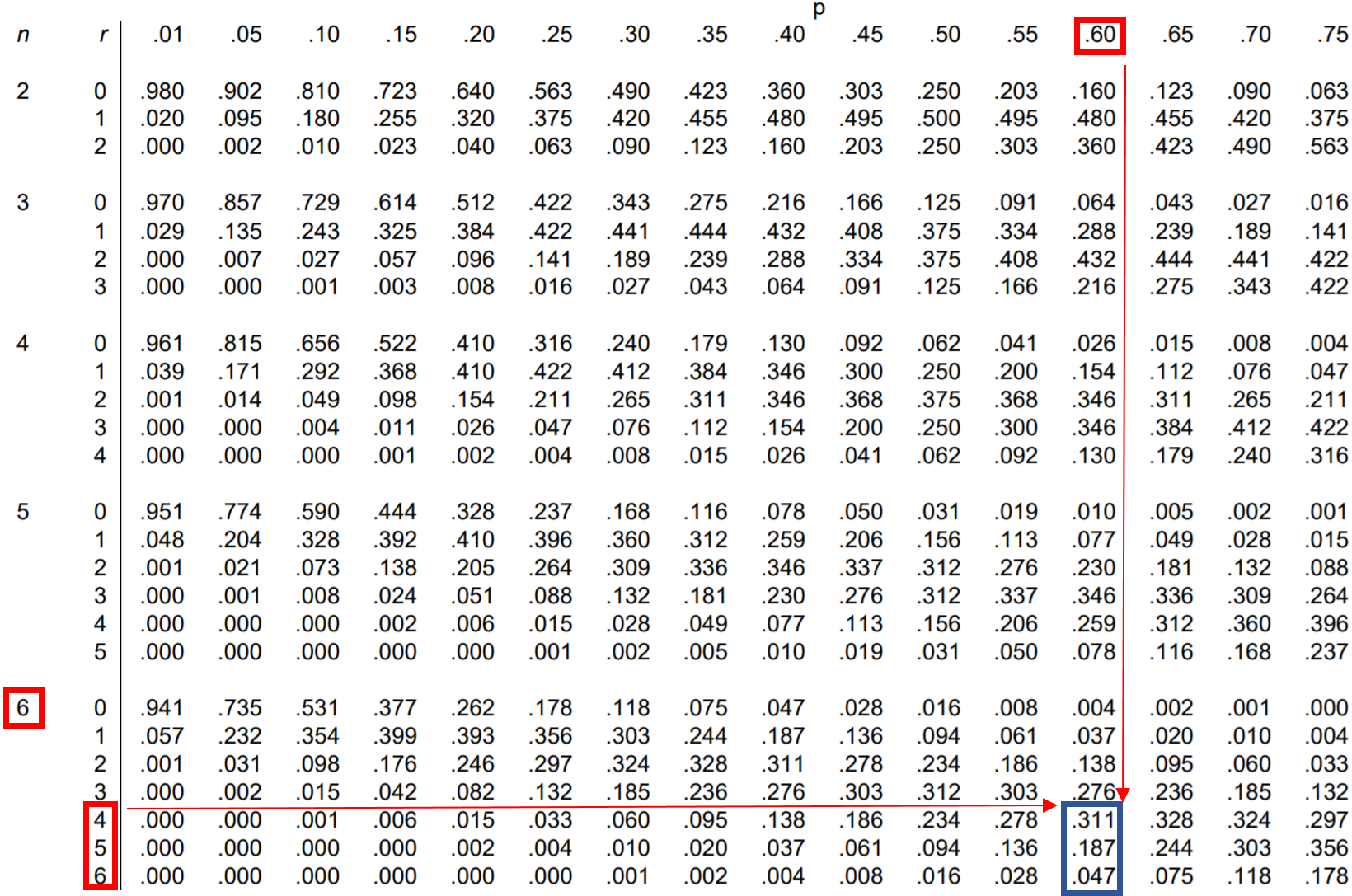
Z tabeli P (daje 4 lub więcej) = 0,311 + 0,187 + 0,047 = 0,545 .

Prawdopodobieństwo, że Jessica wykona 4 lub więcej rzutów wolnych wynosi 0,545 .