Dokładny test fishera: definicja, wzór i przykład
Dokładny test Fishera służy do określenia, czy istnieje istotny związek między dwiema zmiennymi kategorycznymi. Jest powszechnie stosowany jako alternatywa dla testu niezależności chi-kwadrat, gdy liczba co najmniej jednej komórki w tabeli 2 × 2 jest mniejsza niż 5.
Dokładny test Fishera wykorzystuje następujące hipotezy zerowe i alternatywne:
- H 0 : (hipoteza zerowa) Te dwie zmienne są niezależne.
- H 1 : (hipoteza alternatywna) Te dwie zmienne nie są niezależne.
Załóżmy, że mamy następującą tabelę 2×2:
| Grupa 1 | Grupa 2 | Linia ogółem | |
| Kategoria 1 | MA | B | a+b |
| Kategoria 2 | vs. | D | c+d |
| Całkowita kolumna | a+c | b+d | a+b+c+d = n |
Jednostronną wartość p dla dokładnego testu Fishera oblicza się w następujący sposób:
p = (a+b)!(c+d)!(a+c)!(b+d)! / (a!b!c!d!n!)
Daje to tę samą wartość p, co CDF rozkładu hipergeometrycznego z następującymi parametrami:
- wielkość populacji = n
- „sukces” populacji = a+b
- wielkość próbki = a + c
- przykłady „sukcesu” = jeden
Obliczenie dwustronnej wartości p w dokładnym teście Fishera jest trudniejsze i nie można jej znaleźć poprzez zwykłe pomnożenie jednostronnej wartości p przez dwa. Aby znaleźć dwustronną wartość p, zalecamy skorzystanie z kalkulatora testu dokładnego Fishera .
Dokładny test Fishera: przykład
Załóżmy , że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej. Bierzemy prostą losową próbę 25 wyborców i pytamy ich o preferencje dotyczące partii politycznych. Wyniki badania prezentuje poniższa tabela:
| Demokrata | Republikański | Całkowity | |
| Mężczyzna | 4 | 9 | 13 |
| Kobieta | 8 | 4 | 12 |
| Całkowity | 12 | 13 | 25 |
Krok 1: Zdefiniuj założenia.
Dokładny test Fishera przeprowadzimy przy następujących założeniach:
- H 0 : Preferencje dotyczące płci i partii politycznych są niezależne.
- H 1 : Płeć i preferencje partii politycznych nie są niezależne.
Krok 2: Obliczenie dwustronnej wartości p.
Możemy użyć dokładnego kalkulatora testu Fishera, wprowadzając następujące dane:
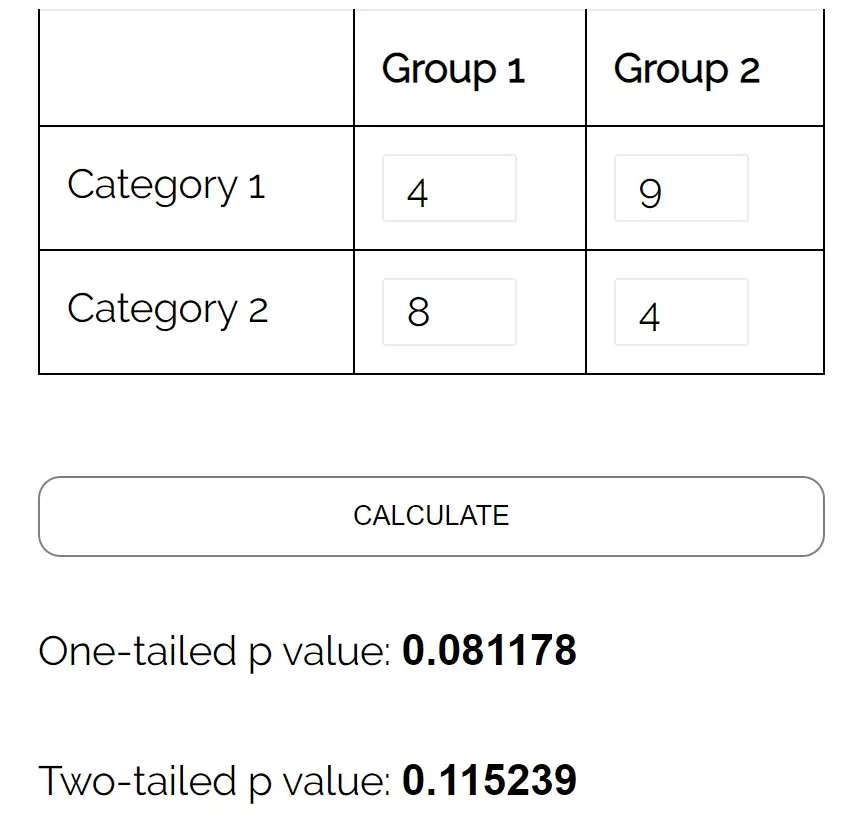
Dwustronna wartość p wynosi 0,115239 . Ponieważ wartość ta jest mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że istnieje statystycznie istotny związek między płcią a preferencją partii politycznej.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak przeprowadzić dokładny test Fishera przy użyciu różnych programów statystycznych:
Jak wykonać dokładny test Fishera w R
Jak wykonać dokładny test Fishera w programie Excel
Jak wykonać dokładny test Fishera w Stata
Jak przeprowadzić dokładny test Fishera w SPSS
Jak wykonać dokładny test Fishera w Pythonie
Kalkulator testu dokładnego Fishera