Wprowadzenie do rozkładu poissona

Rozkład Poissona jest jednym z najpopularniejszych rozkładów w statystyce.

Aby zrozumieć rozkład Poissona, pomocne jest najpierw zrozumienie eksperymentów Poissona.

Eksperymenty z rybami

Eksperyment Poissona to eksperyment, który ma następujące właściwości:

• Można policzyć liczbę sukcesów eksperymentu.
• Znana jest średnia liczba sukcesów, które wystąpiły w określonym przedziale czasu (lub przestrzeni).
• Każdy wynik jest niezależny.
• Prawdopodobieństwo wystąpienia sukcesu jest proporcjonalne do wielkości przedziału.

Przykładem eksperymentu Poissona jest liczba urodzeń na godzinę w danym szpitalu. Załóżmy na przykład, że w konkretnym szpitalu odbywa się średnio 10 porodów na godzinę. Jest to eksperyment Poissona, ponieważ ma następujące cztery właściwości:

• Można policzyć liczbę sukcesów eksperymentu – możemy policzyć liczbę urodzeń.
• Znana jest średnia liczba urodzeń, które mają miejsce w określonym przedziale czasu – Wiadomo, że na godzinę przypada średnio 10 urodzeń.
• Każdy wynik jest niezależny – prawdopodobieństwo, że w danej godzinie jedna matka urodzi dziecko, jest niezależne od prawdopodobieństwa, że inna matka urodzi.
• Prawdopodobieństwo powodzenia jest proporcjonalne do wielkości przedziału: im dłuższy odstęp czasu, tym większe prawdopodobieństwo wystąpienia porodu.

Możemy użyć rozkładu Poissona, aby odpowiedzieć na pytania dotyczące prawdopodobieństwa tego eksperymentu Poissona, takie jak:

• Jakie jest prawdopodobieństwo, że w danej godzinie nastąpi więcej niż 12 porodów?
• Jakie jest prawdopodobieństwo, że w ciągu danej godziny nastąpi mniej niż 5 porodów?
• Jakie jest prawdopodobieństwo, że w danej godzinie odbędzie się od 8 do 11 porodów?

Dystrybucja ryb

Rozkład Poissona opisuje prawdopodobieństwo uzyskania k sukcesów w zadanym przedziale czasu.

Jeśli zmienna losowa X ma rozkład Poissona, prawdopodobieństwo, że X = k powodzenia można obliczyć za pomocą następującego wzoru:

P(X=k) = λ ^k * e ^{– λ} / k!

Złoto:

• λ: średnia liczba sukcesów występujących w określonym przedziale czasu
• k: liczba sukcesów
• e: stała równa około 2,71828

Załóżmy na przykład, że w konkretnym szpitalu odbywają się średnio 2 porody na godzinę. Możemy użyć powyższego wzoru, aby określić prawdopodobieństwo przeżycia 0, 1, 2, 3 narodzin itp. w danej godzinie:

P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353

P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707

P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Prawdopodobieństwo dowolnej liczby urodzeń możemy obliczyć aż do nieskończoności. Następnie tworzymy prosty histogram, aby zwizualizować ten rozkład prawdopodobieństwa:

Obliczanie skumulowanych prawdopodobieństw Poissona

Za pomocą powyższego wzoru można łatwo obliczyć pojedyncze prawdopodobieństwo Poissona (np. prawdopodobieństwo, że w szpitalu odbędą się 3 porody w ciągu danej godziny), ale aby obliczyć skumulowane prawdopodobieństwa Poissona, należy dodać prawdopodobieństwa indywidualne.

Załóżmy na przykład, że chcemy poznać prawdopodobieństwo, że w ciągu danej godziny w szpitalu odbędzie się 1 lub mniej porodów. Do obliczenia tego prawdopodobieństwa użyjemy następującego wzoru:

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

Nazywa się to prawdopodobieństwem skumulowanym , ponieważ polega na dodaniu wielu prawdopodobieństw. Skumulowane prawdopodobieństwo wystąpienia k lub mniejszej liczby urodzeń w danej godzinie możemy obliczyć, korzystając z podobnego wzoru:

P(X≤0) = P(X=0) = 0,1353

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767

Możemy obliczyć te skumulowane prawdopodobieństwa dla dowolnej liczby urodzeń aż do nieskończoności. Następnie możemy utworzyć histogram, aby zwizualizować ten skumulowany rozkład prawdopodobieństwa:

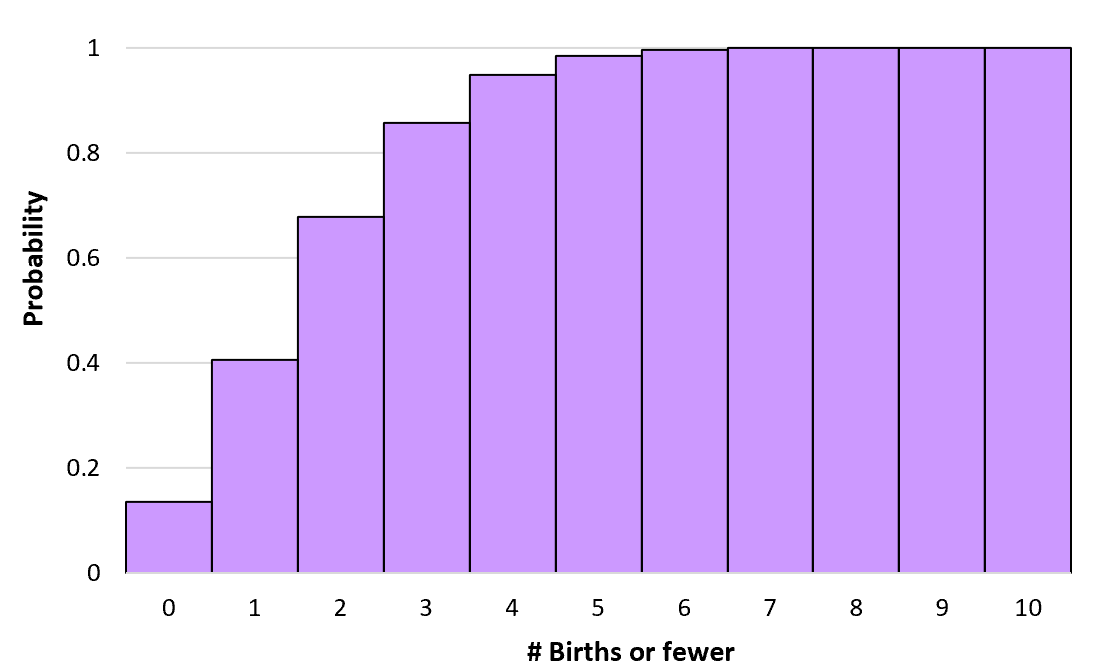
Własności rozkładu Poissona

Rozkład Poissona ma następujące właściwości:

Średnia rozkładu wynosi λ .

Wariancja rozkładu jest również λ .

Odchylenie standardowe rozkładu wynosi √ λ .

Załóżmy na przykład, że w szpitalu odbywają się średnio 2 porody na godzinę.

Średnia liczba urodzeń spodziewanych w danej godzinie wynosi λ = 2 urodzenia.

Wariancja w liczbie urodzeń, której się spodziewamy, wynosi λ = 2 urodzenia.

Problemy praktyki dystrybucji ryb

Skorzystaj z poniższych problemów praktycznych, aby sprawdzić swoją wiedzę na temat rozkładu Poissona.

Uwaga: Do obliczenia odpowiedzi na te pytania użyjemy kalkulatora rozkładu Poissona .

Problem 1

Pytanie: Wiemy, że pewna witryna internetowa generuje 10 sprzedaży na godzinę. Jakie jest prawdopodobieństwo, że w danej godzinie witryna dokona dokładnie 8 sprzedaży?

Odpowiedź: Używając kalkulatora rozkładu Poissona dla λ = 10 i x = 8, stwierdzamy, że P(X=8) = 0,1126 .

Problem 2

Pytanie: Wiemy, że pewien agent nieruchomości dokonuje średnio 5 sprzedaży miesięcznie. Jakie jest prawdopodobieństwo, że w danym miesiącu dokona więcej niż 7 sprzedaży?

Odpowiedź: Używając kalkulatora rozkładu Poissona dla λ = 5 i x = 7, stwierdzamy, że P(X>7) = 0,13337 .

Problem 3

Pytanie: Wiemy, że w pewnym szpitalu odbywają się 4 porody na godzinę. Jakie jest prawdopodobieństwo, że w danej godzinie będą 4 lub mniej porodów?

Odpowiedź: Używając kalkulatora rozkładu Poissona dla λ = 4 i x = 4, stwierdzamy, że P(X≤4) = 0,62884 .

Dodatkowe zasoby

Poniższe artykuły wyjaśniają, jak używać rozkładu Poissona w różnych programach statystycznych:

Jak korzystać z rozkładu Poissona w R
Jak korzystać z rozkładu Poissona w Excelu
Jak obliczyć prawdopodobieństwa Poissona na kalkulatorze TI-84
Rzeczywiste przykłady rozkładu Poissona
Kalkulator dystrybucji ryb