Jak wykonać test t dla dwóch próbek w spss

Test t dla dwóch prób służy do sprawdzenia, czy średnie z dwóch populacji są równe, czy nie.

W tym samouczku wyjaśniono, jak wykonać test t dla dwóch próbek w SPSS.

Przykład: Test t dla dwóch próbek w SPSS

Naukowcy chcą wiedzieć, czy nowy sposób uzdatniania paliwa powoduje zmianę średniego przebiegu na galon danego samochodu. Aby to sprawdzić, przeprowadzają eksperyment, w którym 12 samochodów otrzymuje nowe uzdatnienie paliwa, a 12 samochodów nie.

Poniższy zrzut ekranu pokazuje mpg każdego samochodu wraz z grupą, do której należy (0 = brak uzdatniania paliwa, 1 = uzdatnianie paliwa):

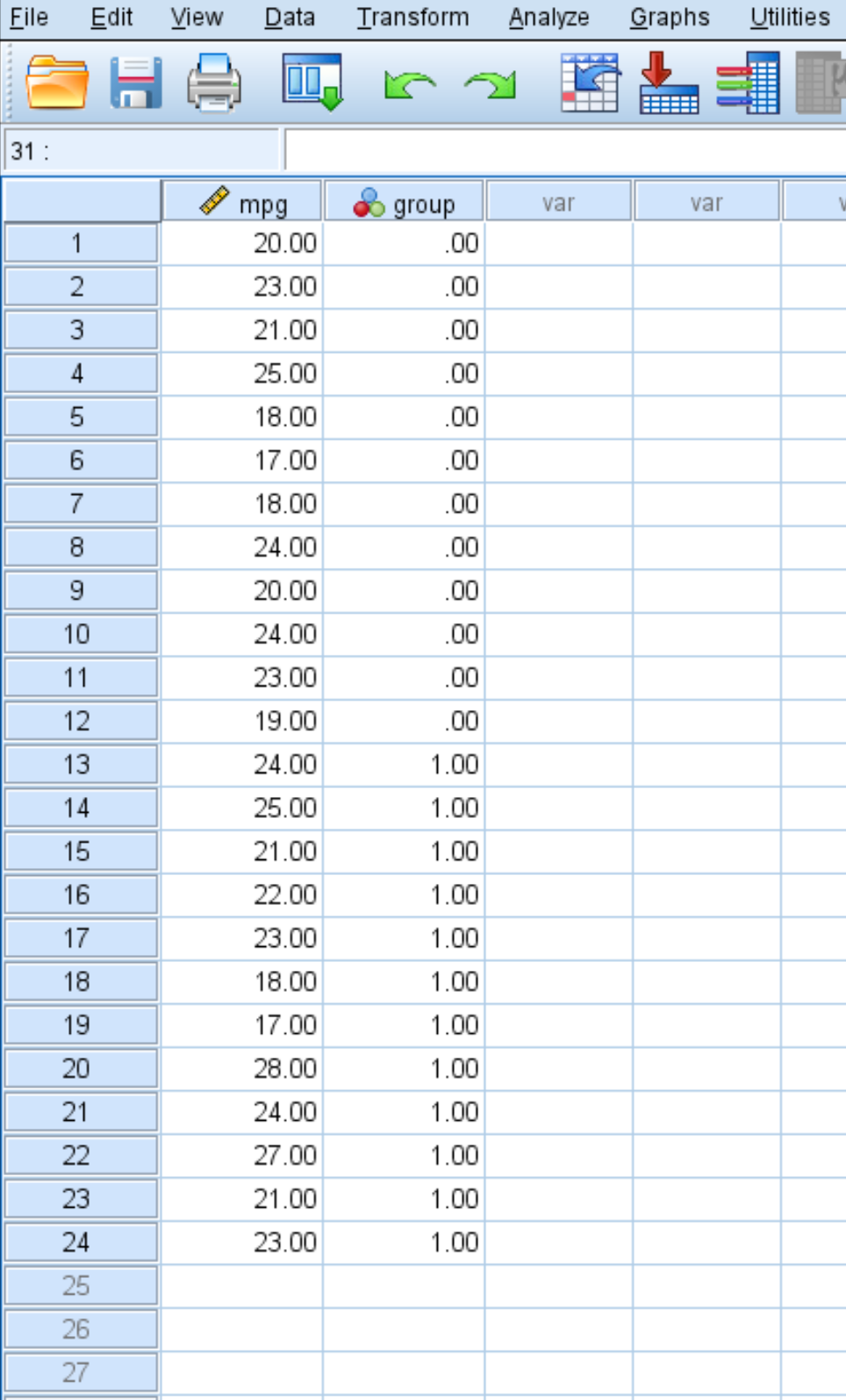
Wykonaj poniższe kroki, aby przeprowadzić test t dla dwóch próbek w celu ustalenia, czy istnieje różnica w średnim przebiegu w mpg pomiędzy tymi dwiema grupami, w oparciu o następujące hipotezy zerowe i alternatywne:

• H ₀ : μ ₁ = μ ₂ (średnie mpg w obu populacjach jest równe)
• H ₁ : μ ₁ ≠ μ ₂ (średnie mpg w obu populacjach nie jest równe)

Użyj poziomu istotności α = 0,05.

Krok 1: Wybierz opcję Test T dla próbek niezależnych.

Kliknij kartę Analiza , następnie Porównaj średnie , a następnie Test T dla niezależnych próbek :

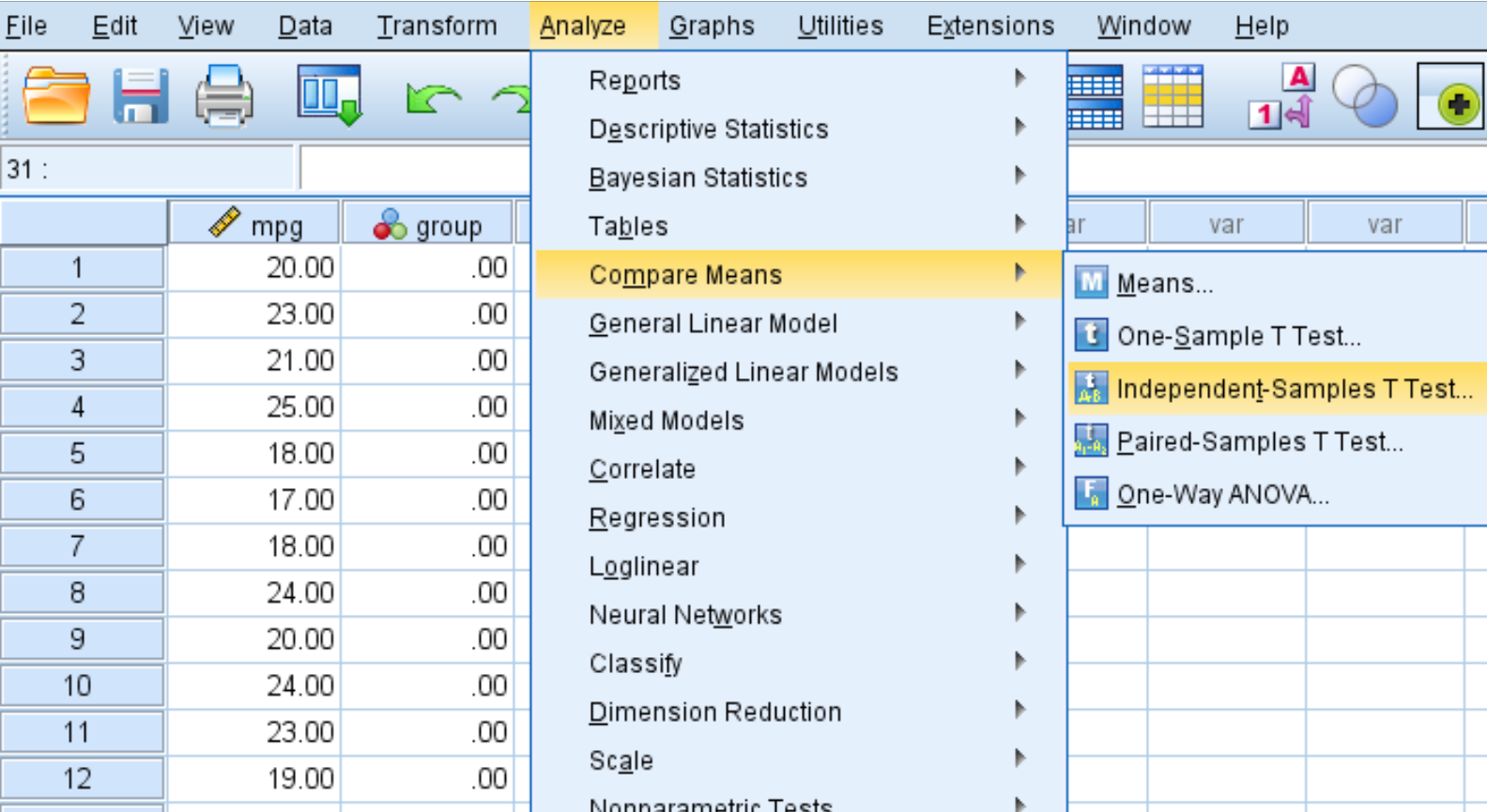
Krok 2: Wpisz wartości potrzebne do wykonania testu t dla dwóch próbek.

Po kliknięciu na Test T dla próbek niezależnych pojawi się następujące okno:

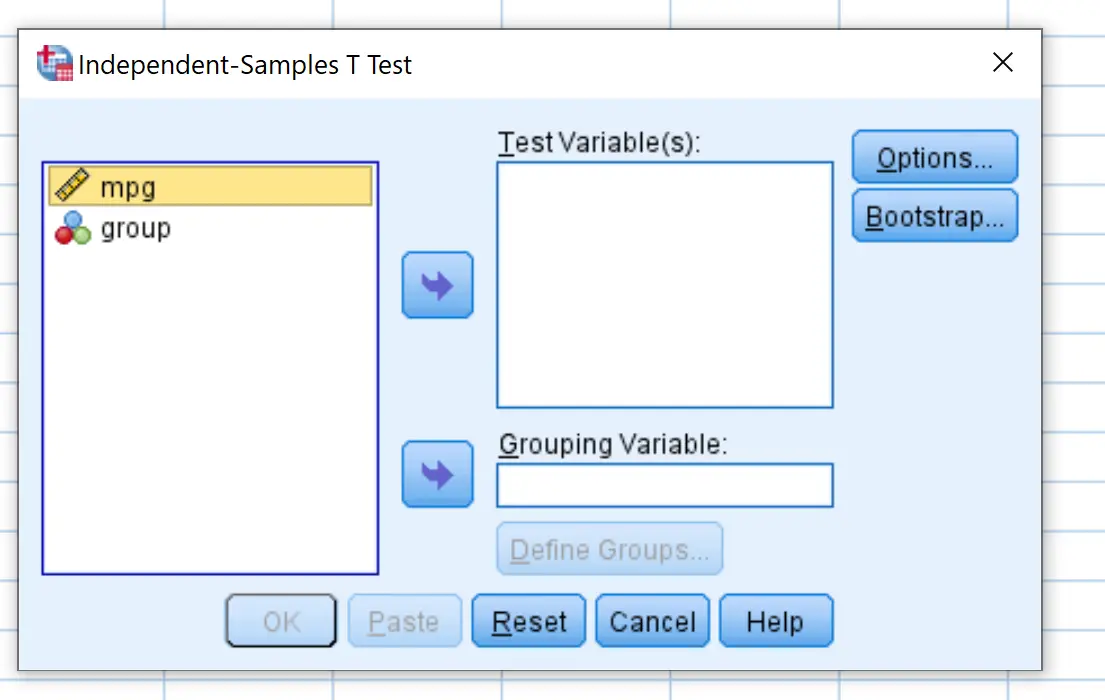
Przeciągnij mpg do pola oznaczonego Zmienne testowe i zgrupuj je w polu oznaczonym Zmienna grupująca . Następnie kliknij Definiuj grupy i zdefiniuj Grupę 1 jako wiersze o wartości 0, a Grupę 2 jako wiersze o wartości 1. Następnie kliknij OK .

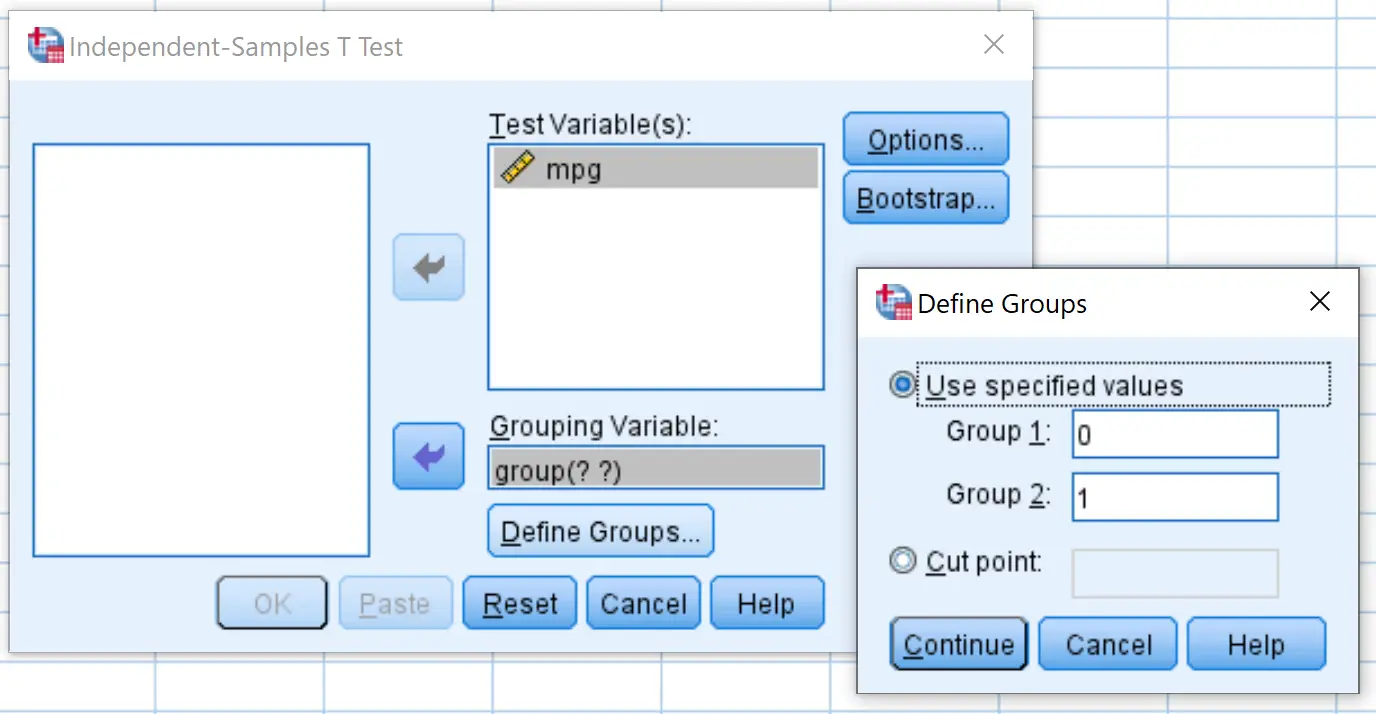
Krok 3: Interpretacja wyników.

Po kliknięciu OK zostaną wyświetlone wyniki dwóch przykładowych testów t:

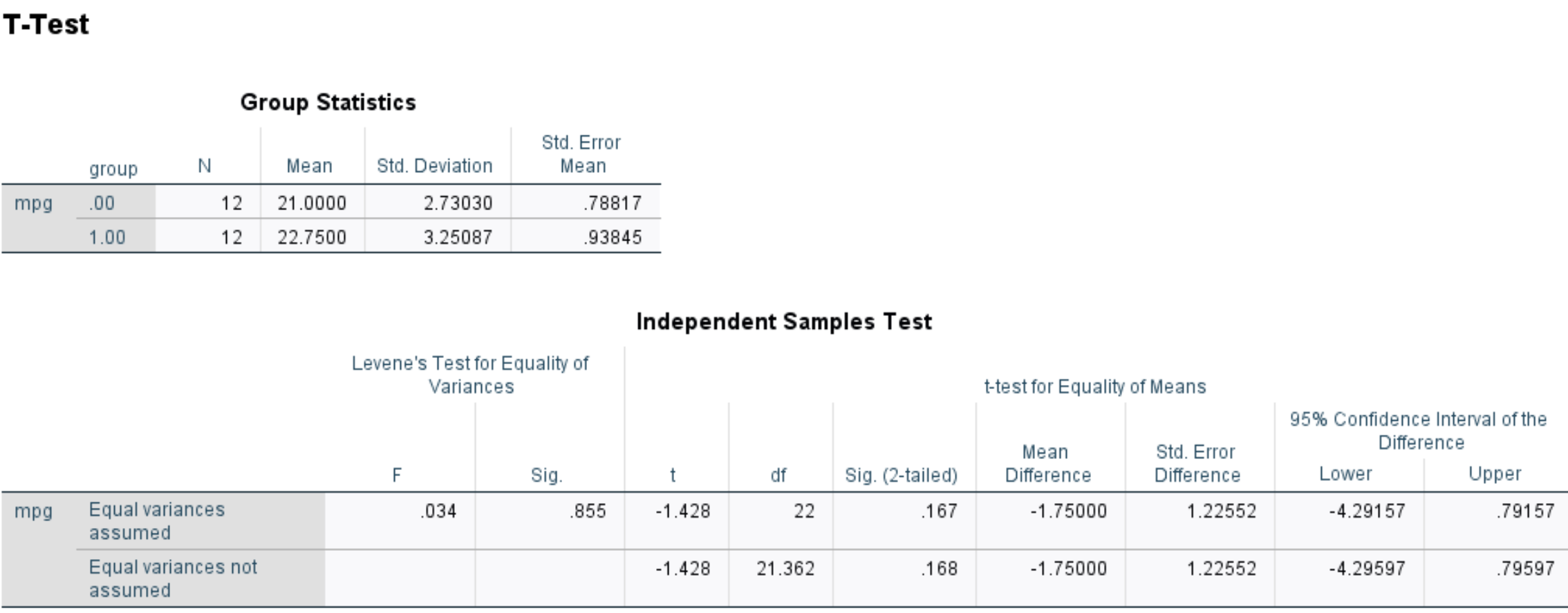
Pierwsza tabela przedstawia następujące statystyki podsumowujące dla obu grup:

• N: Rozmiar próbki
• Średnia: średnia mpg samochodów w każdej grupie
• Standard. Odchylenie: odchylenie standardowe mpg samochodów w każdej grupie
• Standard. Błąd średni: błąd standardowy średniej wartości mpg, obliczony w s/√n

Druga tabela przedstawia wyniki testu t dla dwóch próbek. Pierwszy wiersz pokazuje wyniki testu, jeśli założymy, że wariancja między obiema grupami jest równa. Druga linia pokazuje wyniki testu, jeśli nie przyjmiesz tego założenia.

W tym przypadku obie wersje testu dają niemal identyczne wyniki. Odniesiemy się więc po prostu do wyników pierwszej linii:

• t: Statystyka testowa, która wyniosła -1,428
• df: Stopnie swobody obliczane jako n ₁ + n ₂ -2 = 12+12-2 = 22
• Syg. (dwustronny): Dwustronna wartość p, która odpowiada wartości -1,428 przy df=22
• Średnia różnica: różnica między średnimi z dwóch próbek
• Standard. Błąd różnicowy: błąd standardowy średniej różnicy
• 95% CI różnicy: 95% przedział ufności dla prawdziwej różnicy między średnimi z dwóch populacji

Ponieważ wartość p testu (0,167) jest nie mniejsza niż 0,05, nie udaje nam się odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że rzeczywista średnia wartość mpg różni się w przypadku samochodów poddanych leczeniu i samochodów, które tego nie robią.